Matematika

Štvorcový hranol

2723
369
Alan Milota

Vysvetľujeme, čo je kvadrangulárny hranol, jeho vlastnosti, tváre, vrcholy, okraje, ako vypočítať objem, príklady a cvičenia vyriešené

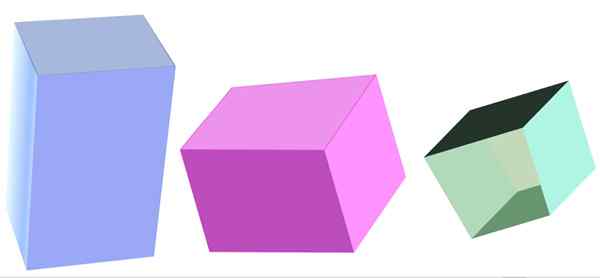
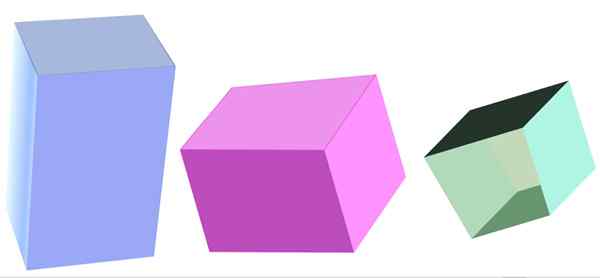Rôzne typy kvadrangulárnych hranolov. Zdroj: f. Zapata

Čo je to kvadrangulárny hranol?

On Štvorcový hranol Je to trojrozmerná geometrická postava rodiny polyhedros. Je tvorená z dvoch rovnakých a rovnobežných tvárí s tvarom kvadrilaterálneho, ako základňa a štyrmi rovnobežníkmi po stranách, celkovo šesť tvárí.

Existuje niekoľko kritérií na ich klasifikáciu, pretože existuje veľa možností pre tvar tvárí a sklonu. Napríklad existujú Rovné domáce hranoly a naklonené kvadrangulárne hranoly.

V prvom prípade sú strany kolmé na základňu a potom sú obdĺžniky alebo štvorce. V druhom prípade sú bočné tváre naklonené vzhľadom na základňu, preto to nemôžu byť obdĺžniky alebo štvorcový.

Okrem toho môže byť kvadrangulárny hranol pravidelný alebo nepravidelný, v závislosti od základne je pravidelný alebo nepravidelný štvoruholník. Pravidelným štvornásobným štvorcom je štvorec, ktorého štyri strany a jeho štyri uhly merajú rovnako .

Príkladom špeciálneho domáceho hranolu je paralelnepiped, ktorého základy sú rovnobežníky. Tvary škatúľ a tehál sú inšpirované kvadrangulárnymi hranolmi, takže dobré príklady, ako použiť túto geometrickú postavu v praktických aplikáciách.

Charakteristiky kvadrangulárneho hranolu

Medzi najdôležitejšie charakteristiky kvadrangulárneho hranolu patrí:

Ich tváre majú polygónový tvar.
Má celkom 6 tvárí (2 bázy a 4 strany), 12 hrán alebo hrany a 8 vrcholov (rohy).
Bočné tváre môžu byť v tvare: štvorcový, obdĺžnik, rovnobežník, rhombus alebo rhomboid.
Jej strany môžu byť rovné (na vnútornej strane je uhol 90 ° uhol s základňami) alebo naklonený (na vnútornej strane je uhol menší ako 90 °).
Bočné tváre priamych hranolov môžu byť iba štvorcové alebo obdĺžniky.
Základy hranolov tiež dostávajú názov pokyny.
Ak je základňa pravidelný štvornásobný, kvadrangulárny hranol je tiež pravidelný. Ako plochá postava je pravidelná, ak majú všetky jeho strany rovnaké opatrenie, jedinou možnosťou je, že základy sú štvorcové.
Ak je základ hranda akékoľvek iné štvoruholníkové odlišné od štvorca, potom sa hranol považuje za nepravidelný.
Pravidelný kvadrangulárny hranol je možné zaregistrovať vo valci.

Môže vám slúžiť: inferenciálna štatistika: História, charakteristiky, na čo je to, príklady

Prvky kvadrangulárneho hranolu

Päť prvkov kvadrangulárneho hranolu je spoločných pre všetky hranoly:

Základne, tvorené dvoma rovnakými a paralelnými štvoruholníkmi.
Bočné tváre, sú štyri rovnobežky, ktoré ohraničujú obrázok.
Vrcholy alebo rohy, bežné body, ktoré majú tri susedné strany hranolu.
Hrany alebo hrany, spoločný segment, ktorý má dve susedné tváre.
Výška: Je to dĺžka kolmého segmentu s koncami v základni. Keď je hranol rovný, výška sa zhoduje s mierou bočných hrán.
Priama časť, oblasť priesečníka medzi hranolom a rovinou, ktorá tvorí 90 ° s bočnými hranami.

Nasledujúci obrázok zobrazuje každý z týchto prvkov pre priamy kvadrangulárny hranol:

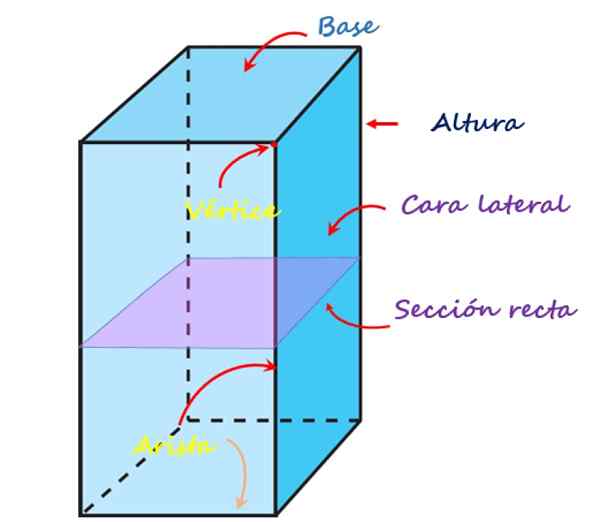Prvky kvadrangulárneho hranolu. Zdroj: f. Zapata

Tváre, vrcholy a hrany

Veľký význam pre štúdium kvadrangulárneho hranolu sú tváre, vrcholy a hrany:

Tváre

Tváre hranolu predstavujú celkom 6: 2 identické bázy v tvare štvornásobného a 4 bočných strán alebo tvárí vo forme rovnobežníka.

Vrcholy

Sú rohy obrázku, bod, v ktorom prichádzajú tri susedné tváre.

Hrany

Sú priesečníkmi medzi tvárami hranolov. Hrany sú klasifikované ako:

Základné hrany, Spoločné segmenty medzi základňami a bočnými tvárami.
Bočné okraje, Ako už názov napovedá, sú to bežné segmenty medzi bočnými tvárami.

Horný obrázok zobrazuje dva typy hrán, označovaných rôznymi farebnými šípkami. Počet hrán n_Do dá sa určiť pomocou Eulerova veta z polyhedros, ktoré sa týkajú počtu hrán s počtom tvárí n_C a vrcholy n_Vložka:

Môže vám slúžiť: matematické funkcie

N_Do = N_C + N_Vložka −2

Pre kvadrangulárny hranol n_C = 6 a n_Vložka = 8, preto:

N_Do = 6 + 8 −2 = 12

Preto počet hrán alebo hrán kvadrangulárneho hranolu je 12.

Ako vypočítať objem kvadrangulárneho hranolu?

Objem hranolu sa chápe ako časť priestoru zamknutého a meria sa v kubických jednotkách, ktoré môžu byť kubické merače, kubické centimetre, kubické nohy alebo iné vhodné, za predpokladu, že sú dĺžky dĺžky kocky.

Objem V je vždy kladné množstvo av prípade akéhokoľvek kvadrangulárneho hranolu je daný produktom medzi základňou základne_b a výška h:

V = a_b × h

Jo) Pravidelný kvadrangulárny objem hranolu

Pretože základne sú štvorcové a štvorec štvorca je jeho bočnou štvorcou:

Do_b = ℓ²

Potom objem hranolu, ktorého výška je „H“, je:

V = ℓ² × h

Ii) Nepravidelný objem hranolu

Závisí to od tvaru základne a výšky „H“ hranolu:

1.- Obdĺžnikový hranol

Oblasť bokov obdĺžnik „A“ a „B“ je:

Do_b = A × B

Takže hlasitosť je:

V = a × b × h

2.- Hranol

Oblasť Rhombus je semifinále jej diagonálov „D“ a „D“:

$A_b=\fracD\cdot d2$

A hlasitosť je:

$V=\left (\fracD\cdot d2 \right )\times h$

3.- Základný hranol Romboid

Základná plocha v tvare Rhomboid je produktom jej základne „B“ a jej relatívnej výšky “h_r„Na túto základňu, ktorá je kolmým segmentom, ktorý prechádza z tejto základne na paralelnú stranu s ňou.

Do_b = B × h_r

Preto objem hranolu s touto základňou je:

Môže vám slúžiť: Aký je sortiment štatistík? (S príkladmi)

V = b × h_r× h

4.- Lichobežník

Pretože oblasť lichobežníka je poloaditom rovnobežných strán „A“ a „B“, vynásobená jeho výškou „C“:

$A_b=\left (\fraca+b2 \right )\times c$

Objem lichobežného hranolu je:

$V=\left (\fraca+b2 \right )\times c\times h$

5.- Základný hranol na bra -capezoid

Oblasť symetrického lichobežníka je semi -produktom jeho diagonálov D a D:

$A_b=\fracD\cdot d2$

V tomto prípade je objem hranolu:

$V=\left (\fracD\cdot d2 \right )\times h$

Cvičenie

Lichobežník kvadrangulárny hranol má objem 648 cm³. Paralelné strany lichobežníka merania a = 10 cm a b = 5 cm, zatiaľ čo výška lichobežníka je c = 6 cm. S týmito údajmi nájdite výšku hranolu.

Riešenie

Pretože rozmery základne majú, vašu oblasť je možné ľahko vypočítať:

$A_b=\left (\fraca+b2 \right )\times c=\left (\frac10 cm+5cm2 \right )\times 6cm=45cm^2$

A vzorec:

V = a_b × h

„H“ sa vyčistí, výška hranolu, pretože jeho objem je známy:

H = v/ a_b = 648 cm³ / 45 cm²= 14.4 cm

Príklady

Obdĺžnikový hranol alebo kocka

Šesť tvárí tohto priameho hranolu je štvorcový alebo obdĺžnikový. Škatule sú príklady obdĺžnikových hranolov, formu, ktorá sa používa aj v mnohých objektoch a konštrukciách, ako sú budovy.

Kocka

Kocka je pravidelný kvadrangulárny hranol, ktorého šesť strán má tvar štvorca, napríklad kock.

Kocka je súčasťou skupiny platonických tuhých látok, geometrických čísel, ktoré spĺňajú dve podmienky. Prvým je, že každá tvár je pravidelným mnohouholníkom a druhá je, že každý vrchol má spoločné rovnaký počet tvárí.

Kocka spĺňa obe podmienky, pretože ich tváre majú štvorcový tvar, ktorý je pravidelným mnohouholníkom. A v každom z ôsmich vrcholov kocky tri tváre toho istého konverge.

Zostávajúce platonické tuhé látky sú Tetrahedron, oktadron, Dodecahedro a Icosaedro.