Deštruktívna interferenčná vzorec a rovnice, príklady, cvičenie

Ten deštruktívne zasahovanie, Vo fyzike sa vyskytuje, keď sú zastarané dve nezávislé vlny, ktoré sa kombinujú v rovnakej oblasti priestoru. Potom hrebene jednej z vĺn spĺňa údolia druhého a výsledkom je vlna s nulovou amplitúdou.

Niekoľko vĺn prechádza bez problémov rovnakým bodom v priestore a potom každá z nich sleduje svoju cestu bez toho, aby bola ovplyvnená, ako sú vlny vo vode nasledujúceho obrázku:

postava 1. Dažďové kvapky produkujú vlny na povrchu vody. Keď majú výsledné vlny nulovú šírku, hovorí sa, že rušenie je deštruktívne. Zdroj: Pixabay.

Predpokladajme, že dve vlny s rovnakou amplitúdou a frekvencii Ω, ktoré zavoláme a budeme volať a₁ a a a₂, ktoré možno opísať matematicky prostredníctvom rovníc:

a₁= Sen (kx -Ω)

a₂ = Sen (kx -Ωt + φ)

Druhá vlna a₂ Má medzeru φ vzhľadom na prvú. Keď sú kombinované, pretože vlny sa dajú prekrývať bez problémov, vedú k výslednej vlne zvanej vlny a_R:

a_R = y₁ + a₂ = Sen (kx -Ω) + sin (kx -Ωt + φ)

Prostredníctvom trigonometrickej identity:

sin a + sin β = 2 sin (a + β)/2 . cos (a - β)/2

Rovnica pre a_R Transformuje sa v:

a_R = [2a cos (φ/2)] sin (kx - ωt + φ/2)

Teraz má táto nová vlna výslednú amplitúdu_R = 2a cos (φ/2), čo závisí od fázového rozdielu. Keď tento fázový rozdiel získa hodnoty+π alebo -π, výsledná amplitúda je:

Do_R = 2a cos (± π/2) = 0

Pretože cos (± π/2) = 0. Presne potom je, keď dôjde k deštruktívnemu rušeniu medzi vlnami. Všeobecne platí, že ak je argument kosínu vo forme ± kπ/2 s nepárny k, amplitúda na_R  Je to 0.

[TOC]

Príklady deštruktívneho rušenia

Ako sme videli, keď dve alebo viac vĺn prechádzajú súčasne cez bod, prekrývajú sa, čo vedie k výslednej vlne, ktorej amplitúda závisí od fázového rozdielu medzi účastníkmi.

Môže vám slúžiť: lineárna variácia: koncept, príklady, vyriešené cvičenie

Výsledná vlna má rovnakú frekvenciu a číslo vlny ako pôvodné vlny. V nasledujúcej animácii sú dve vlny prekrývané v modrej a zelenej farbe. Výsledná vlna je v červenej farbe.

Amplitúda rastie, keď je rušenie konštruktívne, ale zrušuje sa, keď je deštruktívne.

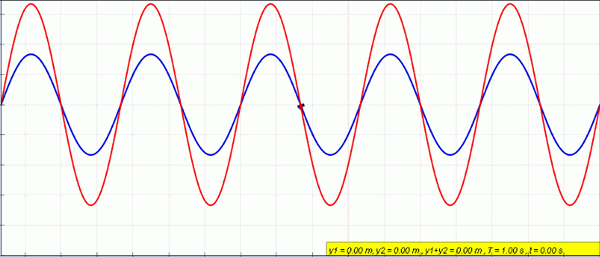Obrázok 2. Modré a zelené zafarbené vlny sa prekrývajú, aby vznikli červenú vlnu. Zdroj: Wikimedia Commons.

Vlny, ktoré majú rovnakú amplitúdu a frekvenciu koherentné vlny, Pokiaľ medzi nimi udržiavajú rovnaký fázový rozdiel φ. Príkladom koherentnej vlny je laserové svetlo.

Podmienka deštruktívneho rušenia

Keď sú modré a zelené vlny zastarané v 180 ° v danom bode (pozri obrázok 2), znamená to, že keď sa pohybujú, majú fázové rozdiely φ π Radianes, 3π radiány, 5π radiány atď.

Týmto spôsobom, rozdelením argumentu výslednej amplitúdy o 2, výsledkom je (π/2) radiány, (3π/2) radiány ... a kosínus takýchto uhlov je vždy 0. Preto je rušenie deštruktívne a amplitúda sa uskutoční 0.

Deštruktívne zasahovanie vlny vo vode

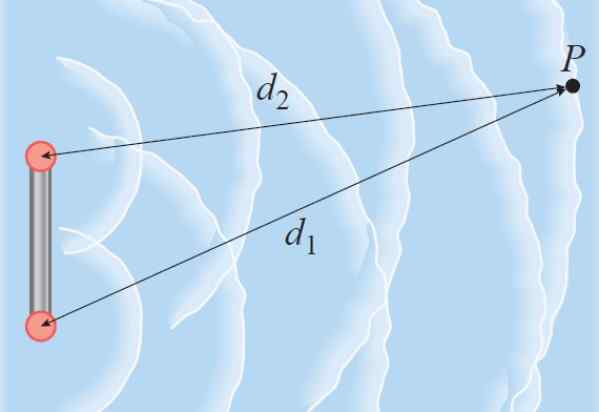
Predpokladajme, že dve koherentné vlny začínajú v jednej druhej. Takéto vlny môžu byť tie, ktoré sa šíria vodou vďaka dvomi barmi, ktoré vibrujú. Ak tieto dve vlny cestujú do toho istého bodu P, prehliadajú rôzne vzdialenosti, fázový rozdiel je úmerný rozdielu cesty.

Obrázok 3. Vlny produkované dvoma zdrojmi cestujú vo vode do bodu P. Zdroj: Giambattista, a. Fyzika.

Ako vlnová dĺžka λ sa rovná rozdielu Radians 2π, potom je pravda, že:

│D₁ - d₂│ / λ = fázový rozdiel / Radiány 2π

Fázový rozdiel = 2π x│D₁ - d₂│/ λ

Môže vám slúžiť: polarizácia svetla: typy, príklady, aplikácie

Ak je cesta ciest zvláštnym počtom vlnových semi-vlny, to znamená: λ/2, 3λ/2, 5λ/2 a tak ďalej, interferencia je deštruktívne.

Ale ak je rozdiel na ceste počet vlnových dĺžok, interferencia je konštruktívne a amplitúdy sa pridajú v bode P.

Deštruktívne rušenie svetelných vĺn

Svetelné vlny môžu navzájom zasahovať, ako uvádza Thomas Young v roku 1801 prostredníctvom svojho oslavovaného experimentu s dvojitým štrbinom.

Young dal svetlo cez štrbinu vyrobenú na nepriehľadnej obrazovke, ktorá podľa princípu Huygens zase generuje dva sekundárne svetelné zdroje. Tieto zdroje pokračovali na ceste cez druhú nepriehľadnú obrazovku s dvoma štrbinami a výsledné svetlo bolo premietané na stenu.

Diagram je pozorovaný na nasledujúcom obrázku:

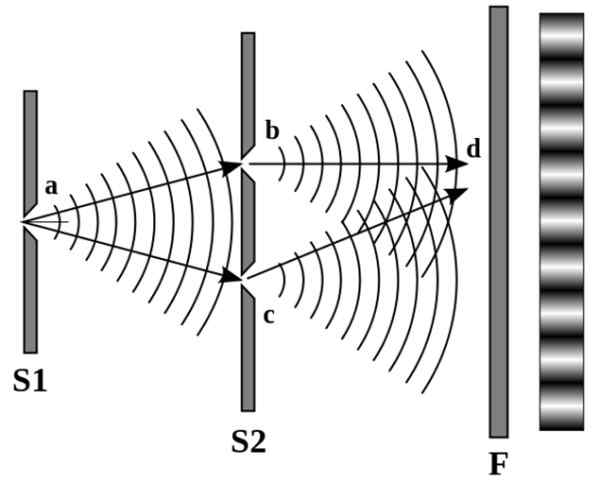Obrázok 4. Vzor svetlých a tmavých čiar na pravej stene je spôsobený konštruktívnym a deštruktívnym rušením, v danom poradí. Zdroj: Wikimedia Commons.

Mladí pozorovali výrazný vzorec alternatívnych svetla a tmavých čiar. Keď zdroje svetla interferujú deštruktívne, čiary sú tmavé, ale ak to robia konštruktívne, čiary sú jasné.

Ďalším zaujímavým príkladom rušenia sú mydlové bubliny. Jedná sa o veľmi tenké filmy, v ktorých dochádza k interferencii, pretože svetlo sa odráža a láma na povrchoch, ktoré obmedzujú film SOAP, a to tak nad a pod.

Obrázok 5. Na filme tenkého mydla sa vytvára interferenčný vzor. Zdroj: pxfuel.

Ako je film hrubý. Výsledkom je vzor farieb, ak je dopadajúce svetlo biele.

Je to preto, že biele svetlo nie je monochromatické, ale obsahuje všetky vlnové dĺžky (frekvencie) viditeľného spektra. A každá vlnová dĺžka vyzerá ako iná farba.

Môže vám slúžiť: svetelné telá: Charakteristiky a spôsob, akým generujú svoje vlastné svetlo

Cvičenie

Dvaja identickí rečníci prevádzkovaní rovnakým oscilátorom sú oddelené 3 metre a jeden poslucháč je vzdialený 6 metrov od stredu oddelenia medzi reproduktormi, v bode alebo.

Potom prejdite do bodu P, v kolmej vzdialenosti 0.350 bodu alebo, ako je to znázornené na obrázku. Prestaň počúvať zvuk prvýkrát. Aká je vlnová dĺžka, v ktorej emituje oscilátor?

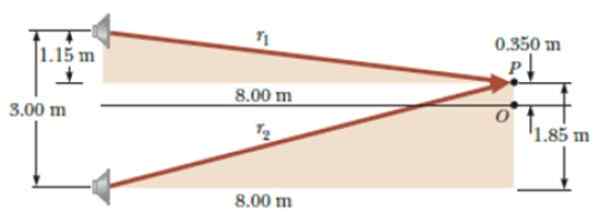Obrázok 6. Diagram pre cvičenie vyriešené. Zdroj: Serway, r. Fyzika pre vedu a inžinierstvo.

Riešenie

Amplitúda výslednej vlny je 0, preto je rušenie deštruktívne. Musíš:

Fázový rozdiel = 2π x│r₁ - r₂│/ λ

Podľa vety Pythagory aplikovaná na tieňované trojuholníky obrázku:

r₁ = √1.pätnásť² + 8² M = 8.08 m; r₂ = √1.85² + 8² M = 8.21 m

│r₁ - r₂│ = │8.08- 8.21 │ m = 0.13 m

Minimácie sa vyskytujú v λ/2, 3λ/2, 5λ/2 ... prvý zodpovedá λ/2, potom vzorca pre fázový rozdiel je:

λ = 2π x│r₁ - r₂│/ fázový rozdiel

Ale fázový rozdiel medzi vlnami musí byť π, takže amplitúda na_R = 2a cos (φ/2) byť nulová, potom:

λ = 2π x│r₁ - r₂│/ π = 2 x 0.13 m = 0.26 m

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 7. Vlny a kvantová fyzika. Editoval Douglas Figueroa (USB).
2. Fisicalab. Interferencia vlny. Získané z: Fisicalab.com.
3. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
4. Serway, r. Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Wikipedia. Rušenie spánku. Zdroj: Je to.Wikipedia.orgán.