Kváznosť vzorec a rovnice, príklady, cvičenie

Ten ohodnotenie, kvázi rozptyl alebo nezdravá rozptyl je štatistická miera rozptylu údajov a vzorka Pokiaľ ide o priemer. Vzorka zase pozostáva zo série údajov prevzatých z hlavného vesmíru, nazývané populácia.

Je označený niekoľkými spôsobmi, tu bol vybraný siež_c² A na jeho výpočet nasleduje nasledujúci vzorec:

postava 1. Definícia kvázivity. Zdroj: f. Zapata.

Kde:

-siež_c ² = kváziancia alebo rozptyl vzorky (rozptyl vzorky)

-X_Jo = Každá zo vzorových údajov

-n = počet pozorovaní

-X = Priemer vzorky

Pretože jednota vzorovej kváznosti je štvorec jednotky, v ktorej prichádza vzorka, v čase interpretácie výsledkov, ktoré sa uprednostňuje, aby pracovala s kvázi štandardná odchýlka alebo štandardná odchýlka vzorky.

Toto sa označuje ako siež_c A získa sa extrahovaním druhej druhej kvázivariancie:

siež_c = √ s_c ²

Kváziriance je podobná rozptylu siež², s jediným rozdielom, že v menovateľovi je to N-1, zatiaľ čo v rozptyle je rozdelený iba do n. Je zrejmé, že keď je n veľmi veľké, hodnoty oboch majú tendenciu byť rovnaké.

Keď je známa hodnota kvázoriancie, môžete okamžite vedieť, že je o rozptyle.

[TOC]

Príklady kváznosti

Chcete poznať charakteristiky akejkoľvek populácie: ľudia, zvieratá, rastliny a všeobecne akýkoľvek typ predmetov. Analýza celej populácie však nemusí byť ľahká úloha, najmä ak je počet prvkov veľmi veľký.

Potom sa odoberia vzorky s nádejou, že ich správanie odráža správanie obyvateľstva, a tak sa o ňom dokážu urobiť závery, vďaka ktorým sú zdroje optimalizované. Toto je známe ako Štatistický záver.

Tu je niekoľko príkladov, v ktorých kváziancia a štandardná odchýlka spojená s kvázi slúžia ako štatistický ukazovateľ zdôraznením, že výsledky získané s ohľadom na priemer.

Môže vám slúžiť: obvod kruhu: Ako ho vytiahnuť a vzorce, vyriešené cvičenia

1.- Marketingový riaditeľ spoločnosti, ktorá vyrába automobilové batérie, musí v mesiacoch odhadnúť priemerné trvanie batérie.

Ak to chcete urobiť, náhodne vyberte vzorku 100 kúpených batérií tejto značky. Spoločnosť si ponecháva záznamy o údajoch kupujúcich a môže s nimi pohovoriť, aby poznala trvanie batérií.

Obrázok 2. Kuasívne hodnotenie je užitočné na výrobu záverov a kontroly kvality. Zdroj: Pixabay.

2.- Akademické riadenie univerzitnej inštitúcie musí odhadnúť registráciu nasledujúceho roka a analyzovať počet študentov, od ktorých sa očakáva, že budú schváliť predmety, ktoré sú v súčasnosti.

Napríklad z každej z oddielov, ktoré v súčasnosti študujú fyzický predmet I, môže adresa zvoliť vzorku študentov a analyzovať jej výkon v uvedenom predsedovi. Týmto spôsobom môžete odvodiť, koľko študentov bude študovať fyziku II v nasledujúcom období.

3.- Skupina astronómov zameriava svoju pozornosť na časť oblohy, kde sa pozoruje určitý počet hviezd s určitými charakteristikami: veľkosť, hmotnosť a teplota napríklad.

Stojí za to sa opýtať, či hviezdy v inom podobnom regióne budú mať rovnaké vlastnosti, vrátane hviezd v iných galaxiách, ako sú susedné oblaky Magallanes alebo Andromeda.

Prečo rozdeliť medzi n-1?

V kvázoriante je rozdelený medzi N-1 namiesto n A je to preto, že kváziancia je a Trval na na tom, Ako je uvedené na začiatku.

Stáva sa, že z rovnakej populácie je možné extrahovať veľa vzoriek. Rozptyl každej z týchto vzoriek je možné spriemerovať, ale priemer týchto odchýlok sa neukáže rovný rozptylu populácie.

Môže vám slúžiť: relatívna hodnota

V skutočnosti má priemer odchýlok vzorky tendenciu podceňovať rozptyl populácie, pokiaľ sa nepoužíva N-1 Menovateľ. Dá sa overiť, že očakávaná hodnota kvázivity e (s_c²) je presne S².

Z tohto dôvodu sa hovorí, že kváziancia je instenovaná a je lepším odhadcom rozptylu populácie s².

Alternatívny spôsob výpočtu kvazného hodnotenia

Ľahko sa demonštruje, že kváziance sa dá vypočítať aj takto:

siež_c² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Štandardné skóre

Tým, že odchýlka od vzorky vieme, koľko štandardných odchýlok má konkrétnu hodnotu x, buď nad alebo pod priemerom.

Na tento účel sa používa nasledujúci bezrozmerný výraz:

Štandardné skóre = (x - x) / s_c

Cvičenie

Vypočítajte kvázianciu a kvázi -typickú odchýlku nasledujúcich údajov, ktoré pozostávajú z mesačných platieb v $, ktorú poisťovňa uskutočnila na súkromnej klinike.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Použite definíciu kváznosti uvedenú na začiatku a tiež overte výsledok alternatívnou formou uvedenou v predchádzajúcej časti.

b) Vypočítajte štandardné skóre druhých údajov, čítanie zhora nadol.

Roztok

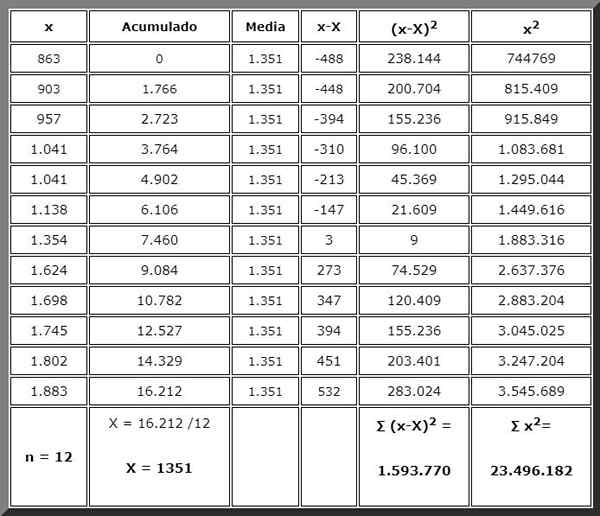
Tento problém sa dá vyriešiť ručne pomocou jednoduchej alebo vedeckej kalkulačky, pre ktorú musíme pokračovať v poriadku. A za to nič lepšie ako usporiadanie údajov v tabuľke, ako je uvedená nižšie:

Vďaka tabuľke, ktoré ste organizovali informácie, a množstvá, ktoré budú potrebné vo vzorcoch, sú na konci príslušných stĺpcov, pripravené na okamžité použitie. Súčty sú označené tučným písmom.

Môže vám slúžiť: Aké sú 7 prvkov obvodu?

Priemerný stĺpec sa vždy opakuje, ale stojí za to, pretože je vhodné mať hodnotu v zobrazení, naplniť každý riadok tabuľky.

Nakoniec sa uplatňuje rovnica pre kvázianciu uvedenú na začiatku, vymenia sa iba hodnoty a pokiaľ ide o sumu, už sme ju vypočítali:

siež_c² = 1.593.770 / (12-1) = 1.593.770/11 = 144.888.2

Toto je hodnota kvázoriancie a jej jednotky sú „doláre štvorcové“, čo nedáva veľa praktického zmyslu, takže sa vypočíta štandardné kvasidy vzorky, čo nie je nič viac ako druhá odmocnina kvázivariancie:

siež_c = (√144.888,2) $ = 380,64 $

Okamžite sa potvrdzuje, že táto hodnota sa získa aj s alternatívnou formou kvázivátnosti. Potrebná suma je na konci posledného stĺpca vľavo:

siež_c² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ jedenásť]

= 2.136.016,55 - 1.991.128,36 = 144.888 dolárov na druhú

Je to rovnaká hodnota získaná s vzorec daný na začiatku.

Riešenie B

Druhá hodnota zhora nadol je 903, jej štandardné skóre je

Štandardné skóre 903 = (x - x) / s_c = (903 - 1351)/380.64 = -1.177

Odkazy

1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
4. Opatrenia. Získané z: Thales.CICA.je.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.