Aký je štatistický rozsah? (S príkladmi)

On rozsah, Prehliadka alebo amplitúda v štatistike je rozdiel (odčítanie) medzi maximálnou hodnotou a minimálnou hodnotou súboru údajov zo vzorky alebo populácie. Ak rozsah s písmenom R a dátami sú reprezentované pomocou X, Vzorec pre rozsah je jednoducho:

R = x_maximálny - X_blesk

 Kde x_maximálny Je to maximálna hodnota údajov a x_blesk Je to minimum.

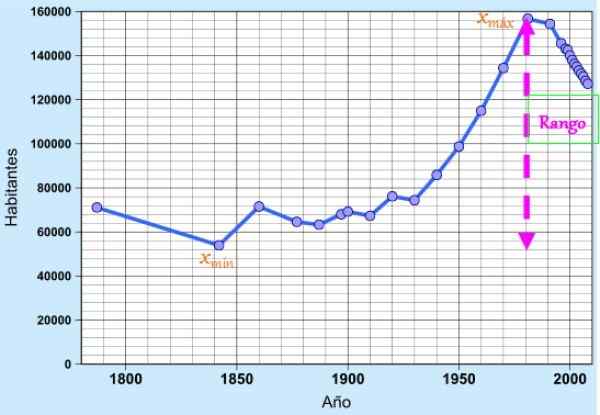
postava 1. Rozsah údajov zodpovedajúcich populácii Cádiz v posledných dvoch storočiach. Zdroj: Wikimedia Commons.

Koncept je veľmi užitočný ako jednoduché disperzné opatrenie na rýchle ocenenie variability údajov, pretože naznačuje rozšírenie alebo dĺžku intervalu, kde sa nachádzajú.

Predpokladajme napríklad, že postava skupiny 25 mužov študentov prvého ročníka inžinierstva na univerzite. Najvyšší študent v skupinových opatreniach 1.93 ma najnižšia 1.67 m. Toto sú extrémne hodnoty údajov o vzorke, preto ich trasa je:

R = 1.93 - 1.67 m = 0.26 m alebo 26 cm.

Postava študentov tejto skupiny je distribuovaná v celom rozsahu.

[TOC]

Výhody a nevýhody

Rozsah je, ako sme už uviedli, miera toho, ako sú rozptýlené údaje. Malý rozsah naznačuje, že údaje sú viac -menej blízke a disperzia je malý. Na druhej strane, väčší rozsah naznačuje, že údaje sú viac rozptýlené.

Výhody výpočtu rozsahu sú zrejmé: je veľmi jednoduché a rýchle nájsť, pretože je to jednoduchý rozdiel.

Má tiež rovnaké jednotky ako údaje, s ktorými funguje, a koncept sa veľmi ľahko interpretuje pre každého pozorovateľa.

V príklade postavy študentov inžinierstva, ak by bol rozsah 5 cm, povedali by sme, že študenti majú rovnakú veľkosť. Ale s rozsahom 26 cm okamžite predpokladáme, že vo vzorke sú študenti všetkých stredných pozícií. Má tento predpoklad vždy správny?

Môže vám slúžiť: rozdiel medzi kruhom a obvodom (s príkladmi)

Nevýhody rozsahu ako disperzné opatrenie

Ak sa pozrieme pozorne, v našej vzorke 25 inžinierskych študentov, iba jedna z nich opatrenia 1.93 a zvyšných 24 má pozície takmer 1.67 m.

A predsa tento rozsah zostáva rovnaký, hoci je úplne možné, že sa vyskytuje opak: že postava väčšiny osciluje okolo 1.90 ma iba jedna miera 1.67 m.

V každom prípade je distribúcia údajov veľmi odlišná.

Nevýhody rozsahu ako disperzného opatrenia sú spôsobené skutočnosťou, že používa iba extrémne hodnoty a ignoruje všetky ostatné. Keďže väčšina informácií sa stráca, neexistuje potuchy, ako sa distribuujú vzorové údaje.

Ďalšou dôležitou črtou je, že rozsah vzorky sa nikdy neznižuje. Ak pridáme ďalšie informácie, to znamená, zvažujeme viac údajov, rozsah sa zvyšuje alebo zostáva rovnaký.

A v každom prípade je užitočné iba pri práci s malými vzorkami, jeho jedinečné použitie sa neodporúča ako miera disperzie vo veľkých vzorkách.

Je potrebné urobiť doplnenie výpočtu ďalších disperzných opatrení, ktoré zohľadňujú informácie poskytnuté celkovými údajmi: trasa Interkartilický, rozptyl, štandardná odchýlka a koeficient variácie.

Interquiriliová trasa, kvartily a vyriešený príklad

Uvedomili sme si, že slabosť rozsahu ako disperzného opatrenia je, že využíva iba extrémne hodnoty distribúcie údajov a vynecháva ostatné.

Aby sa tomu zabránilo, kvartily: tri hodnoty známe ako poloha.

Distribuujú údaje, ktoré nie sú zoskupené do štyroch častí (iné široko používané opatrenia na pozíciu sú Decil a percentá). Toto sú jeho vlastnosti:

-Prvý kvartil q₁ Je to hodnota údajov tak, že 25 % všetkých z nich je menšie ako Q₁.

Môže vám slúžiť: konštanta proporcionality: čo je, výpočet, cvičenia

-Druhý kvartil q₂ Je to stredný distribúcie, čo znamená, že polovica (50 %) údajov je nižšia ako táto hodnota.

-Nakoniec tretí kvartil q₃ poukazuje na to, že 75 % údajov je menšie ako Q₃.

Potom je interquotilný rozsah alebo medzikvartilová trasa definovaná ako rozdiel medzi tretím kvartilom Q₃ a prvý kvartil q₁ údajov:

Interquotilná cesta = r_Otázka = Q₃ - Otázka₁

Týmto spôsobom hodnota hodnosti r_Otázka Nie je to tak ovplyvnené extrémnymi hodnotami. Preto je vhodné používať ho, pokiaľ ide o skreslené distribúcie, napríklad veľmi vysoké alebo veľmi nízke študenti opísané vyššie.

- Výpočet

Existuje niekoľko spôsobov, ako ich vypočítať, tu navrhneme, ale v každom prípade je potrebné poznať počet objednávok "N_ani“, Čo je miesto, ktoré zaberá príslušný kvartil v distribúcii.

To znamená, ak napríklad termín zodpovedajúci Q₁ je druhý, tretí alebo štvrtý a tak na distribúciu.

Prvý kvartil

N_ani (Q₁) = (N+1) / 4

Druhý kvartil alebo stredný

N_ani (Q₂) = (N+1) / 2

Tretí kvartil

N_ani (Q₃) = 3 (n+1) / 4

Kde n je číslo údajov.

Medián je hodnota, ktorá je priamo uprostred distribúcie. Ak je číslo údajov čudné, nie je problém s jeho nájdením, ale ak je to rovnomerné, potom sa tieto dve centrálne hodnoty spriemerujú, aby sa zmenili na jednu.

Po vypočítaní čísla objednávky sa dodržiava jedno z týchto troch pravidiel:

-Ak nemáte desatinné miesta, hľadajú sa údaje uvedené v distribúcii a toto bude štvrtý prehľadaný.

-Ak je číslo objednávky na polceste medzi dvoma, potom sa spriemerujú údaje uvedené v celej časti s nasledujúcou skutočnosťou a výsledkom je zodpovedajúci kvartil.

-V ktoromkoľvek inom prípade je najbližšie celé číslo zaoblené a to bude štvrté miesto.

Môže vám slúžiť: Aditívny princíp

Vyriešený príklad

Na stupnici od 0 do 20, skupina 16 matematických študentov, som získala v čiastočnej skúške nasledujúce známky (body):

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Nájsť:

a) Dáta alebo dátová trasa.

b) hodnoty kvartilov q₁ a Q₃

c) Rozsah interquartil.

Obrázok 2. Urobte kvalifikáciu tejto matematickej skúšky takú variabilitu? Zdroj: Pixabay.

Roztok

Prvá vec, ktorú treba urobiť pre nájdenie trasy, je objednať si zvyšovanie alebo zníženie údajov. Napríklad v rastúcom poradí máte:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Cez vzorec uvedený na začiatku: r = x_maximálny - X_blesk

R = 20 - 1 body = 19 bodov.

Podľa výsledku majú tieto známky veľkú disperziu.

Riešenie B

N = 16

N_ani (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Je to číslo s desatinnými miestami, ktorých celá časť je 4. Potom ideme na distribúciu, údaje, ktoré zaberá štvrté miesto, sa hľadajú a jeho hodnota je spriemerovaná s hodnotou piatej pozície. Pretože obidve sú 9, priemer je tiež 9 a potom:

Otázka₁ = 9

Teraz opakujeme postup na nájdenie q₃:

N_ani (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Opäť je to desatinné miesto, ale keďže nie je na polceste, je zaokrúhlený na 13. Hľadaný kvartil zaberá trinásť pozícií a je:

Otázka₃ = 16

Riešenie c

R_Otázka = Q₃ - Otázka₁ = 16 - 9 = 7 bodov.

To, ako vidíme, je oveľa menšie ako rozsah údajov vypočítaný v oddiele A), pretože minimálne hodnotenie bolo 1 bod, čo je hodnota oveľa ďalej od zvyšku.

Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
3. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
4. Príklady kvartilov. Zdroj: Mathematics10.slepo.
5. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
6. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.