Opatrenia ústrednej tendencie pre zoskupené vzorce údajov, cvičenia

Ten trendové opatrenia ústredný Označujú hodnotu, okolo ktorej sú údaje distribúcie. Najznámejší je priemer alebo aritmetický priemer, ktorý spočíva v pridávaní všetkých hodnôt a vydelení výsledku celkovým počtom údajov.

Ak však distribúcia pozostáva z veľkého počtu hodnôt a nie je prezentovaná usporiadaným spôsobom, nie je ľahké vykonať potrebné výpočty na extrahovanie cenných informácií, ktoré obsahujú.

postava 1. Ústredná tendencia opatrenia pre zoskupené údaje je dobrým indikáciou všeobecného správania dát

Preto sú zoskupené do tried alebo kategórií, aby rozpracovali a distribúcia Frekvencia. Vykonanie tohto predchádzajúceho poradia údajov, potom je ľahšie vypočítať ústredné opatrenia tendencie, medzi ktoré patria:

-Polovica

-Stredný

-Formovať

-Geometrický priemer

-Harmonický priemer

Vzorce

Ďalej máme vzorce ústredných opatrení tendencie pre zoskupené údaje:

Aritmetický priemer

Priemer je najviac použitý na charakterizáciu kvantitatívnych údajov (numerické hodnoty), hoci je dosť citlivý na hodnoty extrémnej distribúcie. Vypočíta sa:

S:

-X: Priemer alebo priemerná aritmetika

-F_Jo: Frekvencia triedy

-m_Jo: Značka triedy

-G: Číslo tried

-N: Celkové údaje

Stredný

Na jeho výpočet je potrebné nájsť interval, ktorý obsahuje pozorovanie N/2 a Interpolárny, aby sa určilo numerickú hodnotu uvedeného pozorovania pomocou nasledujúceho vzorca:

Kde:

-C: Šírka intervalu, ku ktorej medián patrí

-B_M: Dolná hranica uvedeného intervalu

-F_m: Počet pozorovaní obsiahnutých v intervale

-N/2: Celkové údaje vydelené 2.

-F_BM: Počet pozorovaní pred intervalom obsahujúcim medián.

Preto je medián mierou polohy, to znamená, rozdeľuje súbor údajov na dve časti. Môžu byť tiež definované kvartily, Decil a percentá, To rozdelí distribúciu na štyri, desať a sto častí.

Môže vám slúžiť: Fourierov transformácia: Vlastnosti, aplikácie, príklady

Formovať

V zoskupených údajoch sa hľadá trieda alebo kategória, ktorá obsahuje väčšinu pozorovaní. To je Modálna trieda. Distribúcia môže mať dva alebo viac módy, v takom prípade sa volá bimodálny a Multimodálny, respektíve.

Môžete tiež vypočítať módu v zoskupených údajoch podľa rovnice:

S:

-L₁: Dolná hranica triedy, kde je móda

-Δ₁: Zostáva medzi frekvenciou modálnej triedy a frekvenciou triedy, ktorá jej predchádza.

-Δ₂: Odčítať sa medzi frekvenciou modálnej triedy a frekvenciou triedy, ktorá ju nasleduje.

-C: Šírka intervalu obsahujúceho módu

Harmonický priemer

Harmonický priemer je označený h. Keď máte sadu n hodnoty x₁, X₂, X₃…, Harmonický priemer je inverzný alebo recipročný aritmetický priemer inverzie hodnôt.

Je ľahšie ho vidieť prostredníctvom vzorca:

A pri zoskupených údajoch sa výraz transformuje na:

Kde:

-H: Harmonický priemer

-F_Jo: Frekvencia triedy

-m_Jo: Značka triedy

-G: Číslo tried

-N = f₁ + F₂ + F₃ +..

Geometrický priemer

Ak máte n kladné čísla x₁, X₂, X₃…, Jeho geometrický priemer sa počíta N-eme produktu všetkých čísel:

V prípade zoskupených údajov je možné preukázať, že desatinný logaritmus geometrického priemerného log G, je daný:

Kde:

-G: Geometrický priemer

-F_Jo: Frekvencia triedy

-m_Jo: Značka triedy

-G: Číslo tried

-N = f₁ + F₂ + F₃ +..

Vzťah medzi H, G a X

Vždy je pravda, že:

H ≤ g ≤ x

Najviac používané definície

Na nájdenie hodnôt opísaných v predchádzajúcich vzorcoch sú potrebné nasledujúce definície:

Časť

Frekvencia je definovaná ako počet opakovaní faktu.

Rozsah

Je to rozdiel medzi hlavnou a menšou hodnotou, prítomný v distribúcii.

Počet tried

Aby sme vedeli, koľko tried zoskupujeme údaje, používame niektoré kritériá, napríklad nasledujúce:

Môže vám slúžiť: 17 odôvodnených problémov

Hranice

Extrémne hodnoty každej triedy alebo intervalu sa nazývajú hranice a každá trieda môže mať obidve dobre definované limity, v takom prípade má nižšiu hranicu a väčšiu. Alebo môže mať otvorené limity, keď je uvedený rozsah, napríklad hodnoty väčšie alebo nižšie ako určité číslo.

Značka triedy

Jednoducho pozostáva zo stredu intervalu a vypočíta sa v priemere hornej hranice a dolnej hranice.

Šírka intervalu

Dáta môžu byť zoskupené do tried rovnakej alebo inej veľkosti, to je šírka alebo amplitúda. Prvá možnosť je najpoužívanejšia, pretože uľahčuje výpočty, hoci v niektorých prípadoch je nevyhnutné, aby triedy mali inú šírku.

Šírka c Z intervalu je možné určiť podľa nasledujúceho vzorca:

C = rozsah / n_c

Kde_c Je to počet tried.

Cvičenie

Nižšie máme sériu meraní rýchlosti v km/h, odobratých s radarom, ktoré zodpovedajú 50 automobilom, ktoré prešli ulicou v určitom meste:

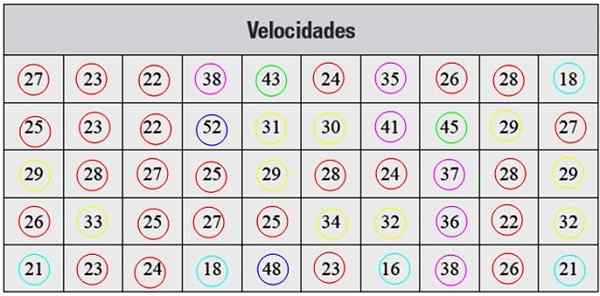Obrázok 2. Tabuľka pre cvičenie vyriešené. Zdroj: f. Zapata.

Riešenie

Predložené údaje nie sú usporiadané, takže prvým krokom je zoskupenie do tried.

Kroky na zoskupenie údajov a zostavenie tabuľky

Krok 1

Nájdite rozsah R:

R = (52 - 16) km/h = 36 km/h

Krok 2

Vyberte počet tried n_c, Podľa daných kritérií. Pretože existuje 50 údajov, môžeme si vybrať n_c = 6.

Krok 3

Vypočítať šírku c intervalu:

C = rozsah /n_c = 36/6 = 6

Krok 4

Triedy formulára a skupinové údaje nasledovne: Pre prvú triedu sa vyberie nižšia hranica, akonáhle sa k tejto hodnote C = 6, predtým vypočítaná, a získa sa horná hranica prvá trieda.

Rovnakým spôsobom vybuduje zvyšky tried, ako je uvedené v nasledujúcej tabuľke:

Môže vám slúžiť: Čo je číslo capicúa? Vlastnosti a príklady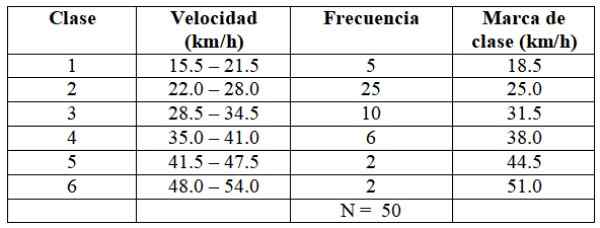

Každá frekvencia zodpovedá farbe na obrázku 2, týmto spôsobom je zabezpečená, že žiadna hodnota unikla z toho, že by bola zohľadnená.

Priemerný výpočet

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Medián výpočtu

Medián je v triede 2 tabuľky, pretože existuje prvých 30 distribučných údajov.

-Šírka intervalu, ku ktorej medián patrí: C = 6

-Nižšia hranica intervalu, kde je medián: b_M = 22.0 km/h

-Počet pozorovaní obsiahnutých v intervale f_m = 25

-Celkové údaje vydelené 2: 50/2 = 25

-Počet pozorovaní pred intervalom obsahujúcim medián: f_BM = 5

A operácia je:

Medián = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/h

Formovať

Móda sa nachádza aj v triede 2:

-Šírka intervalu: C = 6

-Dolná hranica triedy, kde sa nachádza móda: L₁ = 22.0

-Odpočítať frekvenciu modálnej triedy a frekvenciou triedy, ktorá jej predchádza: δ₁ = 25-5 = 20

-Odpočítať medzi frekvenciou modálnej triedy a frekvenciou nasledujúcej triedy: δ₂ = 25 - 10 = 15

S týmito údajmi je operácia:

Móda = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/h

Výpočet geometrického priemeru

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x log 38 + 2 × log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/h

Harmonický priemerný výpočet

1/h = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/h

Zhrnutie opatrení centrálnej tendencie

Jednotky premenných sú km/h:

-Médiá: 29.03

-Medián: 26.80

-Móda: 25.40

-Geometrické médiá: 28.13

-Harmonický priemer: 27.32

Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
3. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
4. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
5. Spiegel, m. 2009. Štatistika. Séria Schaum. 4 ta. Vydanie. McGraw Hill.
6. Liečba zoskupených údajov. Získané z: Itchihuahua.Edu.mx.
7. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.