Priemerné zrýchlenie Ako vypočítané a vyriešené cvičenia

Ten priemerné zrýchlenie do_m Je to veľkosť, ktorá opisuje variáciu rýchlosti častice v priebehu času. Je to dôležité, pretože ukazuje variácie, ktoré pohyb prežíva.

Na vyjadrenie tejto veľkosti matematickým pojmom je potrebné zvážiť dve rýchlosti a dva momenty času, ktoré sú označené ako V₁ a v₂, a t₁ a t₂.

Priemerné zrýchlenie je veľmi dôležitý parameter filmu. Zdroj: Pixabay.

Kombinácia hodnôt podľa ponúkanej definície bude vykonaný nasledujúci výraz:

V medzinárodnom systéme, ak jednotky pre a_m bude m/s², Aj keď budú slúžiť ďalšie jednotky zahŕňajúce dĺžku na jednotku času na druhú.

Napríklad je km/h.S, ktorý znie „kilometer za hodinu a druhý“. Všimnite si, že časová jednotka sa objaví dvakrát. Premýšľanie o mobilu, ktorý sa pohybuje po priamke, to znamená, že pre každú sekundu uplynul mobil zvyšuje svoju rýchlosť o 1 km/h. Alebo klesá o 1 km/h za každú sekundu, ktorá prechádza.

[TOC]

Zrýchlenie, rýchlosť a rýchlosť

Aj keď je to spojené so zrýchlením so zvýšením rýchlosti, pravdou je, že starostlivo pozorovanie definície sa ukázalo, že akákoľvek zmena rýchlosti znamená existenciu zrýchlenia.

A rýchlosť sa nemení vždy vo veľkosti. Môže sa stať, že mobil sa líši iba od smeru a udržuje vašu rýchlosť konštantnú. Za túto zmenu stále existuje zrýchlenie.

Príkladom je auto, ktoré dáva krivku s konštantnou rýchlosťou 60 km/h. Vozidlo podlieha zrýchleniu, ktoré je zodpovedné za zmenu smeru rýchlosti tak, aby vozidlo nasledovalo krivku. Vodič ho aplikuje pomocou volantu.

Takéto zrýchlenie je nasmerované do stredu zakrivenej trajektórie, aby sa auto z toho nedostalo. Prijímať názov zrýchlenia radiálny ani normálny. Ak sa radiálne zrýchlenie náhle zrušovalo, auto už nemohlo dať krivke a pokračovať v priamke.

Môže vám slúžiť: Wimshursst Machine: História, ako to funguje a aplikácie

Auto pohybujúce sa cez krivku je príkladom dvojrozmerného pohybu, zatiaľ čo keď pochoduje v priamke, jeho pohyb je jedno -rozmerný. V tomto prípade je jediným účinkom zrýchlenia zmenu rýchlosti vozidla.

Toto zrýchlenie sa nazýva zrýchlenie tangenciálny. Nie je to exkluzívny pre jednorazový pohyb. Auto, ktoré dáva krivke pri 60 km/h, môže súčasne zrýchliť 70 km/h pri jej užívaní. V tomto prípade vodič musí použiť volant aj pedál akcelerátora.

Ak vezmeme do úvahy jednosmerný pohyb, priemerné zrýchlenie má geometrickú interpretáciu podobnú interpretácii priemernej rýchlosti, ako sklon sušiacej čiary, ktorá znižuje krivku v bodoch P a Q rýchlostného grafu vs. čas.

Toto je vidieť na nasledujúcom obrázku:

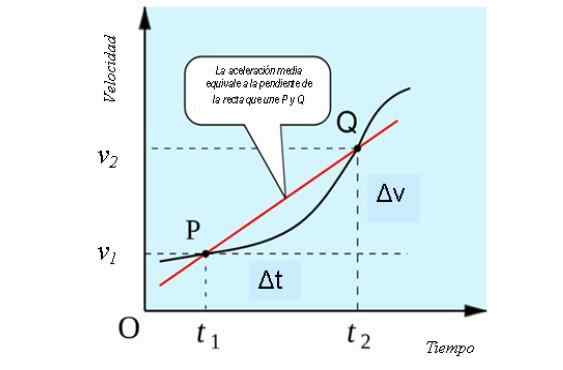Geometrická interpretácia priemerného zrýchlenia. Zdroj: Zdroj: すじにく シチュー [CC0].

Ako sa vypočíta priemerné zrýchlenie

Pozrime sa na niektoré príklady na výpočet priemerného zrýchlenia v rôznych situáciách:

I) V určitom okamihu má mobil, ktorý sa pohybuje po priamke. Aké bolo priemerné zrýchlenie?

Odpoveď

Pretože pohyb je jedno -rozmerný, vektorový zápis sa dá vydať, v takom prípade:

vložka_ani = +25 km/h = +6.94 m/s

vložka_F = -10 km/h = - 2.78 m/s

Δt = 120 s

Kedykoľvek máte cvičenie so zmiešanými veľkosťami, ako je tento, v ktorom sú hodiny a sekundy, je potrebné odovzdať všetky hodnoty rovnakým jednotkám.

Keďže je jednosmerným pohybom, notácia vektora bola vydaná.

Ii) cyklista sa pohybuje na východ rýchlosťou 2.6 m/s a o 5 minút neskôr ide na juh na 1.8 m/s. Nájdite svoje priemerné zrýchlenie.

Môže vám slúžiť: Vy Canis Majoris: Objav, charakteristiky, štruktúra, školenie a vývoj

Odpoveď

Pohyb nie je jedno -rozmerový, preto sa používa zápis vektora. Jednotkové vektory Jo a J Uvádzajú adresy vedľa nasledujúceho dohovoru o znakoch, čo uľahčuje výpočet:

• Sever: +J
• Juh: -J
• Toto: +Jo
• Západ: -Jo

vložka₂ = - 1.8 J pani

vložka₁ = + 2.6 Jo pani

Δt = 5 minút = 300 sekúnd

Znaky zrýchlenia v jednom -rozmernom pohybe

Ako vždy to, čo sa stane s priemerným alebo priemerným veľkosti, poskytnuté informácie sú globálne. Neposkytujú podrobnosti o tom, čo sa stalo s mobilom v každom okamihu, avšak to, čo prispievajú, zostáva cenné pre opis pohybu.

Prostredníctvom známok rýchlosti a zrýchlenia je možné vedieť, či sa mobil, ktorý sa pohybuje po linke, zrýchľuje alebo brzdí. V obidvoch situáciách je prítomné zrýchlenie, pretože sa menia rýchlosť.

Toto sú niektoré zaujímavé úvahy týkajúce sa príznakov týchto dvoch veľkostí:

• Priemerná rýchlosť a zrýchlenie, obidva rovnaké znamenie, znamená, že mobil videný globálne, mobil sa stáva rýchlejším a rýchlejšie.
• Rýchlosť a zrýchlenie s rôznymi znakmi sú znakom mobilu podpisovanie.

Zvyčajne sa predpokladá, že vždy, keď ide o negatívne zrýchlenie, mobil brzdí. To platí, ak je mobilná rýchlosť pozitívna. Ale ak je negatívny, v skutočnosti sa rýchlosť zvyšuje.

Ako vždy, keď je pohyb študovaný, sa predpokladajú osobitné prípady. Napríklad, čo sa stane, keď je priemerné zrýchlenie nulové?. Znamená to, že mobil si vždy zachoval svoju konštantnú rýchlosť?

Odpoveď je nie. Mobil mohol v uvažovanom intervale meniť svoju rýchlosť, ale počiatočná rýchlosť a finále boli rovnaké. V súčasnosti nie je známy detail toho, čo sa stalo v intervale, pretože priemerné zrýchlenie neponúka viac informácií.

Môže vám slúžiť: Joule Effect: Vysvetlenie, príklady, cvičenia, aplikácie

Čo ak priemerné zrýchlenie do_m Sa rovná zrýchleniu do V ktoromkoľvek okamihu dočasného intervalu? Toto je veľmi zaujímavá situácia nazývaná rektilineárny pohyb rovnomerne rozmanitý alebo MRUV).

Znamená, že rýchlosť sa v priebehu času rovnomerne mení. Preto je zrýchlenie konštantné. V prírode existuje také hnutie, s ktorým sú všetci známe: voľný pád.

Voľný pád: pohyb s neustálym zrýchlením

Je známe, že Zem priťahuje predmety k svojmu stredu a že uvoľnením niektorých v určitej výške zažíva zrýchlenie gravitácie, ktorej hodnota je približne konštantná a rovná 9.8 m/s² blízko povrchu.

Ak odpor vzduchu nezasahuje, pohyb je vertikálny a je známy ako voľný pád. Keď je zrýchlenie konštantné a výber T₀ = 0, priemerná rovnica zrýchlenia sa transformuje na:

Kde sa získa dobre známy vzorec na nájdenie rýchlosti v každom okamihu pádu:

vložka_F = v₀ + At = gt (v₀= 0)

Kde a = g = 9.8 m/s²

Cvičenie

Objekt je spadnutý z dostatočnej výšky. Nájdite rýchlosť po 1.25 sekundy.

Odpoveď

vložka_ani = 0, pretože objekt je zrušený, potom:

vložka_F = Gt = 9.8 x 1.25 m/s = 12.25 m/s, smerované vertikálne smerom k zemi. (Vertikálny smer bol odstránený ako pozitívny).

Keď sa objekt blíži k zemi, jeho rýchlosť sa zvyšuje o 9.8 m/s pre každú uplynutú sekundu. Hmotnosť objektu nie je zapojená. Dva rôzne objekty, spadnuté z rovnakej výšky a zároveň, vyvíjajú rovnakú rýchlosť ako padajú.

Odkazy

1. Giancoli, D. Fyzika. Zásady s aplikáciami. Šieste vydanie. Sála. 21-35.
2. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 20-34.
3. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Vydanie. Mexiko. Redaktori učenia sa Cengage. 21-39.