Bezplatné vektorové vlastnosti, príklady, cvičenia

Ten bezplatné vektory Sú to tie, ktoré sú plne špecifikované svojou veľkosťou, smerom a ich významom, bez toho, aby bolo potrebné označiť bod aplikácie alebo konkrétny pôvod.

Pretože nekonečné vektory možno nakresliť týmto spôsobom, voľný vektor nie je jedinečnou entitou, ale množinou paralelných a identických vektorov, ktoré sú nezávislé od miesta, kde sa nachádzajú.

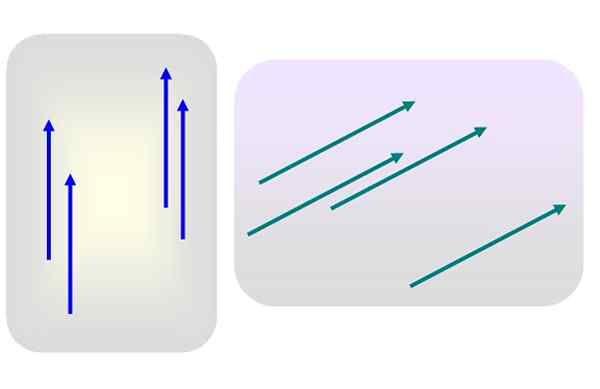
postava 1. Rôzne vektory. Zdroj: Self Made.

Povedzme, že existuje niekoľko vektorov veľkosti 3 smerovaných vertikálne nahor alebo veľkosť 5 a naklonených doprava, ako na obrázku 1.

Žiadny z týchto vektorov nie je špecificky použitý do určitého bodu. Potom ktorýkoľvek z modrých alebo zelených vektorov predstavuje svoju príslušnú skupinu, pretože jej charakteristiky - modul, smer a zmysel - nie sú vôbec upravené, keď sa prenesú na iné miesto lietadla.

Bezplatný vektor je zvyčajne označený v tlačenom texte napríklad malým a odvážnym písmenom vložka. Alebo s malými písmenami a šípkou na vrchu, ak ide o rukopisný text.

[TOC]

 Príklady

Výhodou, ktorú majú voľné vektory, je to, že sa môžu pohybovať lietadlom alebo priestorom a udržiavať svoje vlastnosti, pretože ktorýkoľvek zástupca súboru je rovnako platný.

Preto sa často používajú fyzika a mechanika. Napríklad na označenie lineárnej rýchlosti tuhej látky, ktorá sa pohybuje, nie je potrebné zvoliť konkrétny bod objektu. Potom sa rýchlostný vektor správa ako voľný vektor.

Ďalším príkladom voľného vektora je pár síl. A spárovať Pozostáva z dvoch síl rovnakej veľkosti a smeru, ale z opačných zmyslov, aplikovaných v rôznych bodoch tuhého. Účinkom páru nie je prenášať objekt, ale spôsobiť rotáciu vďaka moment vyrábaný.

Obrázok 2 zobrazuje pár síl aplikovaných na volant. Cez sily F₁ a F₂, Krútiaci moment, ktorý otáča volant okolo jeho stredu, je vytvorený a v pláne.

Môže vám slúžiť: bór nitrid (BN): štruktúra, vlastnosti, získanie, použitia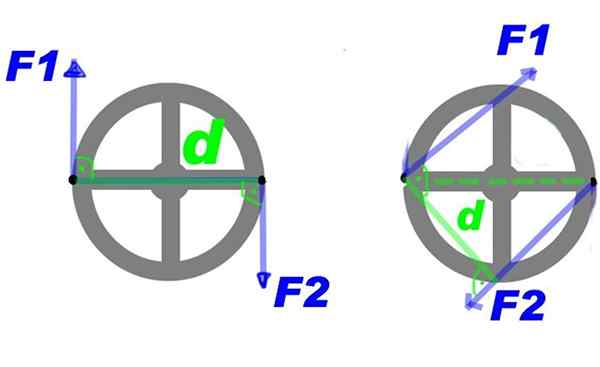 Obrázok 2. Niekoľko síl aplikovaných na volant poskytuje bodovací zákrut. Zdroj: Bensko [verejná doména].

Môžete vykonať nejaké zmeny na páre a naďalej získať rovnaký rotučný účinok, napríklad zvýšiť silu, ale znížiť vzdialenosť medzi nimi. Alebo si udržujte pevnosť a vzdialenosť, ale pár naneste na ďalších pár bodov na volante, to znamená, otočte krútiaci moment okolo stredu.

Čas pár síl alebo jednoducho spárovať, Je to vektor, ktorého modul je FD a je kolmá na kolmo na lietadlo kolesa. V príklade, ktorý je uvedený konventom, má čas na negatívny zmysel.

Vlastnosti a vlastnosti

Na rozdiel od voľného vektora V, vektory AB a CD Sú pevné (pozri obrázok 3), pretože majú určený východiskový bod a bod príchodu. Ale byť vybavením navzájom a postupne s vektorom vložka, Sú reprezentatívnym pre voľný vektor vložka.

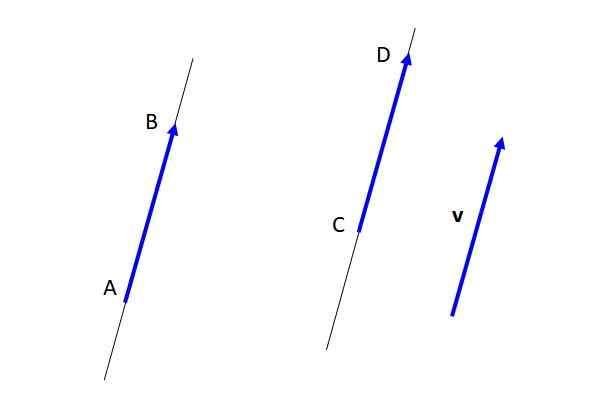Obrázok 3. Bezplatné vektory, vybavenie a pevné vektory. Zdroj: Self Made.

Hlavné vlastnosti bezplatných vektorov sú nasledujúce:

-Akýkoľvek vektor AB (Pozri obrázok 2), ako je uvedené, reprezentatívne pre voľný vektor vložka.

-Modul, smer a význam sú rovnaké v akomkoľvek voľnom zástupcovi vektora. Na obrázku 2 vektory AB a CD Predstavujú bezplatný vektor vložka A sú to vybavenie.

-Vzhľadom na bod P v priestore je vždy možné nájsť bezplatného zástupcu vektora vložka ktorého pôvod je v P a uvedený zástupca je jedinečný. Toto je najdôležitejšia vlastnosť bezplatných vektorov a tá, ktorá ich robí tak univerzálnymi.

Môže vám slúžiť: Európa (satelit): Charakteristiky, zloženie, obežná dráha, pohyb

-Plavbovaný voľný vektor je označený ako 0 A je to súbor všetkých vektorov, ktorý nemá veľkosť, smer a význam.

-Ak vektor AB predstavuje voľný vektor vložka, Potom vektor BA predstavuje voľný vektor -vložka.

-Použije sa notácia Vložka³ určiť súbor všetkých vesmírnych vektorov a Vložka² Určiť všetky voľné vektory lietadla.

Vyriešené cvičenia

S bezplatnými vektormi môžete vykonať nasledujúce operácie:

-Prírastok

-Odčítanie

-Násobenie lezenia vektorom

-Skalárny produkt medzi dvoma vektormi.

-Krížový produkt medzi dvoma vektormi

-Lineárna kombinácia vektorov

A viac.

-Cvičenie 1

Študent má v úmysle plávať z bodu na brehu z jednej rieky do druhej, ktorá je presne vpredu. Na dosiahnutie nič priamo rýchlosťou 6 km / h, v kolmom smere, má však prúd rýchlosť 4 km / h, ktorá ho odvádza.

Vypočítajte rýchlosť vyplývajúcu od plavca a koľko je prúdom odklonený prúdom.

Riešenie

Predĺženie rýchlosti plavca je vektorový súčet jeho rýchlosti (vzhľadom na rieku, nakreslený zvisle nahor) a rýchlosť rieky (nakreslená zľava doprava), ktorá sa vykonáva, ako je uvedené na obrázku nižšie:

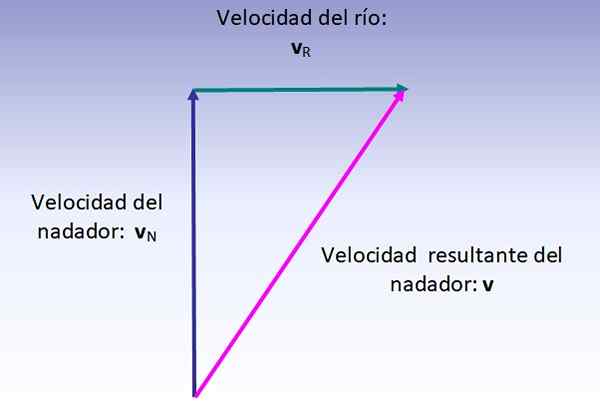
Rozsah výslednej rýchlosti zodpovedá preprava zobrazeného pravého trojuholníka, preto:

V = (6² + 4²) ^½ km/h = 7.2 km/h

Adresa sa dá vypočítať podľa uhla v súvislosti s kolmo na pobrežie:

a = arctg (4/6) = 33.7. alebo 56.Tretí týkajúce sa pobrežia.

Cvičenie 2

Nájdite čas dvojice síl zobrazených na obrázku:

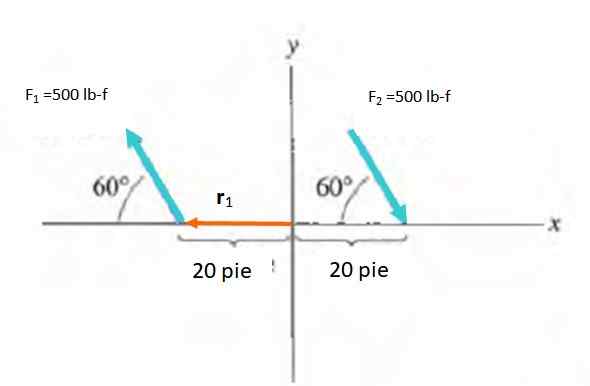
Riešenie

Moment sa vypočíta podľa:

Môže vám slúžiť: Nepreaglastické otrasy: v rozmeroch a príkladoch

M = r X F

Jednotky okamihu sú lb-f.noha. Pretože krútiaci moment je v rovine obrazovky, moment je nasmerovaný kolmá na ňu, buď von alebo dovnútra.

Pretože krútiaci moment príkladu má tendenciu otáčať objekt, na ktorý sa aplikuje (ktorý nie je znázornený na obrázku), tento moment sa posudzuje smerom do obrazovky a s negatívnym znakom.

Veľkosť momentu je m = f.d.hriech A, byť pod uhlom medzi silou a vektorom r. Musíte si vybrať bod, na ktorý by ste mohli vypočítať okamih, ktorý je bezplatným vektorom. Preto je vybraný pôvod referenčného systému r ide z O do bodu použitia každej sily.

M₁ = M₂ = -Fdsen60 ° = -500 . dvadsať .Sen 60 ° lb-f . noha = -8660.3 lb-f . noha

Čistý moment je súčet m₁ a m₂: -17329.5 lb-f . noha.

Odkazy

1. Brada, t. 2011. Úvod do vektorov. Získané z: nrich.Matematika.orgán.
2. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley. 38-52.
3. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika.31-68.
4. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť. 15-53.
6. Kalkulačka kalkulačky vektor. Získané zo: 1728.orgán
7. Vektory. Obnovené z: Je to.Wikibooks.orgán