Výsledný výpočet vektorov, príklady, cvičenia

On výsledný vektor Je to tá, ktorú získala operácia s vektormi, ktorých výsledok je tiež vektor. Normálne je táto operácia súčtom dvoch alebo viacerých vektorov, prostredníctvom ktorých sa získa vektor, ktorého účinok je rovnocenný.

Týmto spôsobom sa výsledkom získajú vektory, ako je rýchlosť, zrýchlenie alebo sila. Napríklad, keď niekoľko síl koná na tele F₁, F₂, F₃,.. . Vektorový súčet všetkých týchto síl je ekvivalentný s čistou silou (výsledná), ktorá sa matematicky vyjadruje:

F₁ + F₂ + F₃ +… = F_R  ani F_N

postava 1. Hmotnosť snehu je distribuovaná nad stropom a jeho účinok môže byť nahradený jedinou výslednou silou aplikovanou na príslušnom mieste. Zdroj: Pixabay.

Výsledný vektor, či už ide o sily alebo akýkoľvek iný vektorový veľkosť, uplatňuje pravidlá súčtu vektorov. Pretože vektory majú okrem numerickej hodnoty smer a zmysel, nestačí pridať moduly, aby mal výsledný vektor.

Platí to iba v prípade, keď sú zapojené vektory v rovnakom smere (pozri príklady). V opačnom prípade je potrebné použiť metódy vektorov, ktoré môžu byť v závislosti od prípadu geometrické alebo analytické.

[TOC]

Príklady

Geometrické metódy na nájdenie výsledného vektora sú metóda polygónu a metóda rovnobežníka.

Pokiaľ ide o analytické metódy, je metóda komponentov, prostredníctvom ktorej je možné nájsť vektor vyplývajúci z akéhokoľvek vektorového systému, pokiaľ máme svoje karteziánske komponenty.

Geometrické metódy na pridanie dvoch vektorov

Predpokladajme vektory alebo a vložka (Označujeme ich odvážne, aby sme ich odlíšili od skalárnych). Na obrázku 2) máme ich umiestnené v lietadle. Na obrázku 2 b) sa presunula k vektorovi V takým spôsobom, že jeho pôvod sa zhoduje s koncom roku alebo. Výsledný vektor prechádza z pôvodu prvého (alebo) na špičku posledného (vložka):

Môže vám slúžiť: stlačiteľnosť: tuhé látky, kvapaliny, plyny, príklady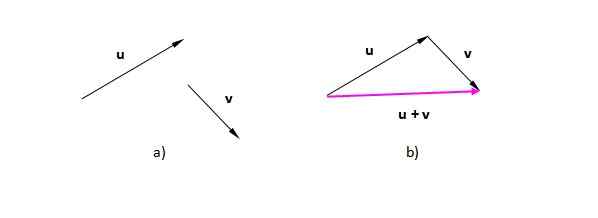 Obrázok 2. Výsledný vektor z grafického súčtu vektorov. Zdroj: Self Made.

Obrázok, ktorý má za následok v tomto prípade, je trojuholník (trojuholník je 3 -vedený polygón). Ak máme dva vektory v rovnakom smere, postup je rovnaký: umiestnite jeden z vektorov za druhým a nakreslite ten, ktorý prechádza z pôvodu alebo chvosta prvého na špičku alebo koniec posledného.

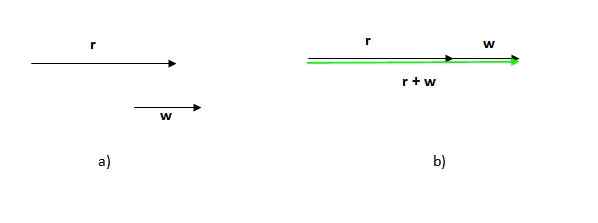
Upozorňujeme, že poradie, v ktorom sa tento postup uskutočňuje.

Tiež si všimnite, že v tomto prípade modul (Dĺžka alebo veľkosť) výsledného vektora je súčet modulov ďalších vektorov, na rozdiel od predchádzajúceho prípadu, v ktorom je výsledný vektorový modul menší ako súčet modulov účastníkov.

Metóda rovnobežníka

Táto metóda je veľmi vhodná, ak potrebujete pridať dva vektory, ktorých body pôvodu súhlasia, s pôvodom súradníckeho systému X-Y. Predpokladajme, že to je prípad našich vektorov alebo a vložka (Obrázok 3):

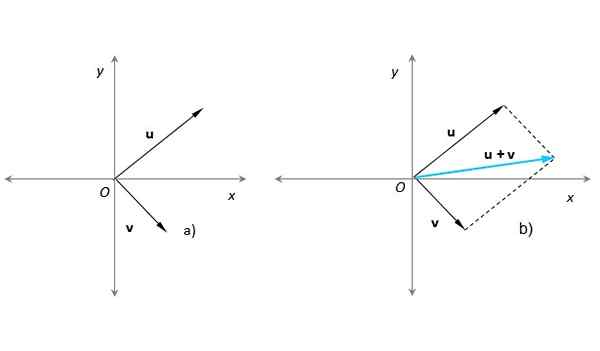Obrázok 3. Súčet dvoch vektorov pomocou rovnobežnej metódy s výsledným vektorom v tyrkysovej modrej farbe. Zdroj: Self Made.

Na obrázku 3b) bol vytvorený rovnobežník pomocou paralelných bodkovaných čiary alebo už vložka. Výsledný vektor má svoj pôvod v O a jeho konci v bode, kde sa bodkované čiary pretínajú. Tento postup je úplne rovnocenný s postupom opísaným v predchádzajúcej časti.

Cvičenia

-Cvičenie 1

Vzhľadom na nasledujúce vektory nájdite výsledný vektor pomocou polygonálnej metódy.

Môže vám slúžiť: svetlo odraz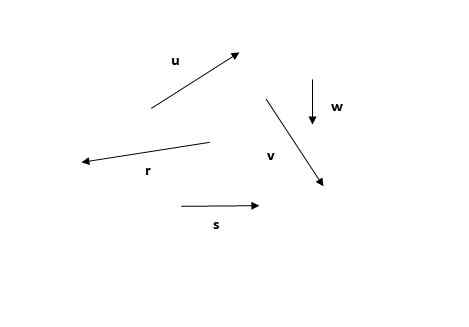 Obrázok 4. Vektory, aby našli, čo je výsledkom polygonálnej metódy. Cvičenie 1. Zdroj: Self Made.

Riešenie

Polygonálna metóda je prvou z pozorovaných metód. Pamätajte, že súčet vektorov je komutatívny (poradie dodatkov nezmení súčet), takže môžete začať s ktorýmkoľvek z vektorov, napríklad s vektormi, napríklad alebo (Obrázok 5a) alebo r (Obrázok 5b):

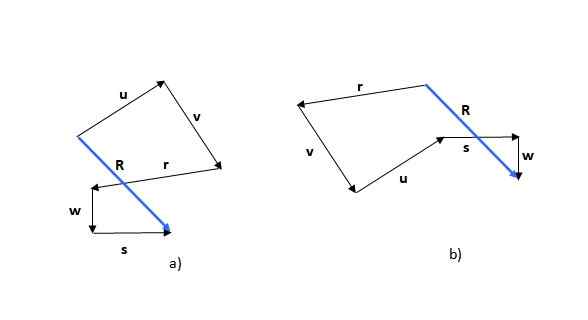Obrázok 5. Súčet vektorov prostredníctvom polygonálnej metódy. Zdroj: Self Made.

Získaný obrázok je polygón a výsledný vektor (v modrej) sa nazýva R. Ak začnete s iným vektorom, formované číslo sa môže líšiť, ako je možné vidieť v príklade, ale výsledný vektor je rovnaký.

Cvičenie 2

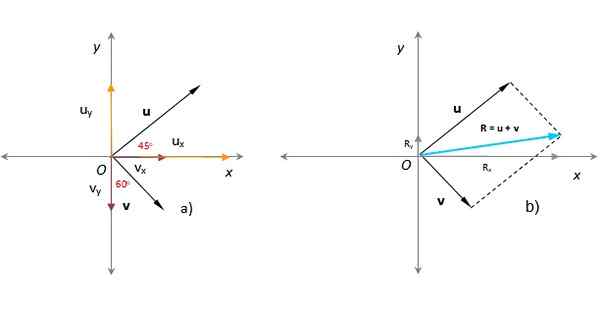
Na nasledujúcom obrázku je známe, že moduly vektorov alebo a vložka respektíve u = 3 ľubovoľné jednotky a v = 1.8 ľubovoľných jednotiek. Uhol, že alebo forma s kladnou osou x je 45 °, zatiaľ čo vložka formujte 60 ° s osou y, ako je vidieť na obrázku. Nájdite výsledný vektor, veľkosť a smer.

Riešenie

V predchádzajúcej časti sa zistil, že výsledný vektor bol použitý metóda rovnobežníka (v tyrkysovej na obrázku).

Jednoduchý spôsob, ako nájsť výsledný vektor analyticky, je vyjadriť vektory pridávanie z hľadiska ich karteziánskych komponentov, čo je ľahká úloha, keď sú známe modul a uhol, ako napríklad vektory tohto príkladu:

alebo_X = u . cos 45 ° = 3 x cos 45 ° = 2.12; alebo_a = u . Sin 45 ° = 3x sen 45 ° = 2.12

vložka_X = v . Sen 60 ° = 1.8 x sen 60 ° = 1.56; vložka_a = -V . cos 60 ° = -1.8 x cos 60 ° = - 0.9

Môže vám slúžiť: kyvadlový pohyb

Vektory alebo a vložka Sú to vektory patriace do lietadla, každá z obidvoch komponentov. Vektor U je v prvom kvadrante a jeho komponenty sú pozitívne, zatiaľ čo vektor V je vo štvrtom kvadrante; Jeho X komponent je pozitívny, ale jej projekcia na vertikálnej osi spadá do osi a negatívna.

Výpočet karteziánskych komponentov výsledného vektora

Výsledný vektor pridáva algebraicky príslušné komponenty X a Y, aby sa získali svoje karteziánske komponenty:

R_X = 2.12 + 1.56 = 3.68

R_a = 2.12 + (-0.9) = 1.22

Akonáhle sú karteziánske komponenty špecifikované a vektor je úplne známy. Výsledný vektor môže byť vyjadrený so zápisom do štvorcových držiakov (zátvorky):

R = ľubovoľné jednotky

Zápis držiaka sa používa na rozlíšenie vektora od bodu v rovine (alebo vo vesmíre). Ďalším spôsobom, ako analyticky vyjadriť výsledný vektor, je použitie jednotkových vektorov Jo a j v lietadle (Jo, J a klimatizovať v priestore):

R = 3.68 Jo + 1.22 J ľubovoľné jednotky

Pretože obe komponenty výsledného vektora sú pozitívne, vektor R Patrí k prvému kvadrantu, ktorý už bol graficky videný.

Veľkosť a smer výsledného vektora

Veľkosť R, známa karteziánskym komponentom R, Vedľa svojich komponentov r_X a r_a Tvoria pravý trojuholník:

Veľkosť alebo modul: r = (3.68² + 1.22²)^½ = 3.88

Adresa Q Berie kladnú os x ako referenciu: q = arcan (r (r_a / R_X) = arctg (1.22/3.68) = 18.Tretí

Odkazy

1. Pridávanie vektorov a pravidiel. Obnovené z: mloka.Fyzický.Unsw.Edu.Au
2. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika.31-68.
3. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť. 15-53.
5. Kalkulačka kalkulačky vektor. Obnovené z: www.1728.orgán