Výpočet vektorov vyrovnávača, príklady, cvičenia

On vyváženie vektora Je to ten, ktorý kontrastuje s výsledným vektorom, a preto je schopný vyvážiť systém, pretože má rovnakú veľkosť a rovnaký smer, ale na rozdiel od tohto.

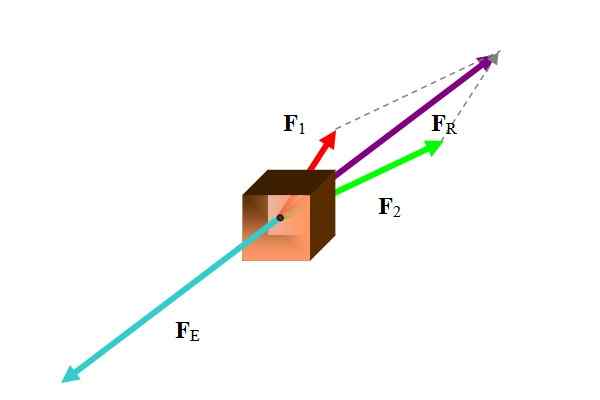
Vyvažovací vektor sa pri mnohých príležitostiach vzťahuje na vektor sily. Na výpočet vyrovnávacej sily je výsledná sila prvá, ako je znázornené na nasledujúcom obrázku:

postava 1. Na tele dva sily, ktorého výsledkom je vyvážené silou v tyrkysovej farbe. Zdroj: Self Made.

Podľa daných údajov existujú rôzne metódy na vykonanie tejto úlohy. Pretože sily sú vektormi, výsledkom je vektorový súčet zúčastnených síl:

F_R = F₁ + F₂ + F₃ +  .. .

Medzi metódy, ktoré sa majú použiť. V príklade bol obrázok použitý metóda rovnobežníka.

Akonáhle je výsledná sila nájdená, vyvažovacia sila je presne opačným vektorom.

Jo F_A Je to vyvažovacia sila, potom je splnená F_A Aplikuje sa v určitom bode, zaručuje rovnováhu prekladu systému. Ak ide o jednu časticu, nebude sa pohybovať (alebo možno to urobí konštantnou rýchlosťou), ale ak ide o rozšírený objekt, bude mať stále možnosť otočiť:

F_R + F_A = 0

[TOC]

Príklady

Vyvažovacie sily sú prítomné na všetkých stranách. Sami sme vyvážení silou, ktorú stolička vyvíja, aby kompenzovala váhu. Objekty nájdené v pokoji: Knihy, nábytok, stropné žiarovky a veľké množstvo mechanizmov sú neustále vyvážené silami.

Môže vám slúžiť: Nepreaglastické otrasy: v rozmeroch a príkladoch

Napríklad, odpočinková kniha na stole je vyvážená normálnou silou, ktorú vyvíja na knihu a bráni jej pádu. To isté platí pre reťazec alebo kábel, ktorý drží žiarovku, ktorá visí zo stropu v miestnosti. Káble, ktoré držia zaťaženie, sú rozložené ich hmotnosť cez napätie v nich.

V tekutine sú niektoré objekty schopné vznášať sa a zostať v pokoji, pretože ich hmotnosť je vyvážená stúpajúcou silou vyvíjanou tekutinou, ktorá sa nazýva TAM.

Rôzne mechanizmy musia byť vyvážené s vedomím vektora vyváženej sily, ako sú stĺpce, lúče a stĺpce.

Pri použití rovnováhy je potrebné nejakým spôsobom vyvážiť hmotnosť objektu s silou, ktorá je rovnocenná, buď pridaním váh alebo pružinami.

Stôl

Tabuľka síl sa používa v laboratóriu na určenie vyváženej sily. Skladá sa z kruhovej plošiny, z ktorej máte horný pohľad na obrázku a ktorý má transportér na meranie uhlov.

Na okrajoch stola sú kladky, cez ktoré reťazce, ktoré držia váhy a ktoré sa zbiehajú v obruči, ktorý je v strede.

Napríklad dve závažia sú zavesené. Napätie generované na reťazcoch týmito hmotnosťami je nakreslené v červenej a modrej na obrázku 2. Tretí váži zelenú, môže vyvážiť výslednú silu ostatných dvoch a udržať systém v rovnováhe.

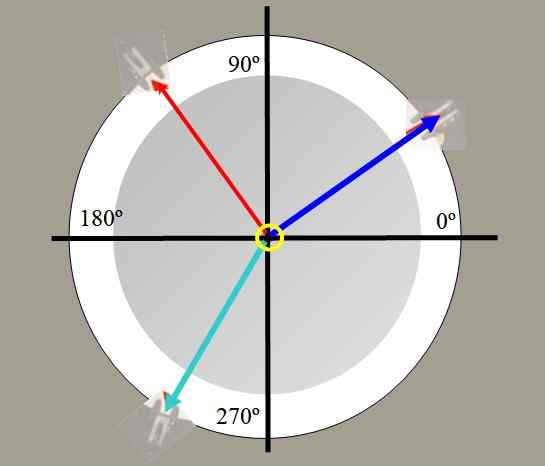Obrázok 2. Pohľad z vrcholu tabuľky síl. Zdroj: Self Made.

S tabuľkou síl môžete overiť vektorový charakter síl, rozložiť sily, nájsť vyvažovaciu silu a overiť Lamyho vetu:

Môže ti slúžiť: slnko

Ak Telo je v rovnováhe vďaka trom koplany, súbežných a nekolineálnych (neatralelných) síl, ktoré sa nazývajú Do, B a C, Vzťah medzi týmito silami je nasledujúci:

A/ sin α = b/ sen β = c/ sen γ

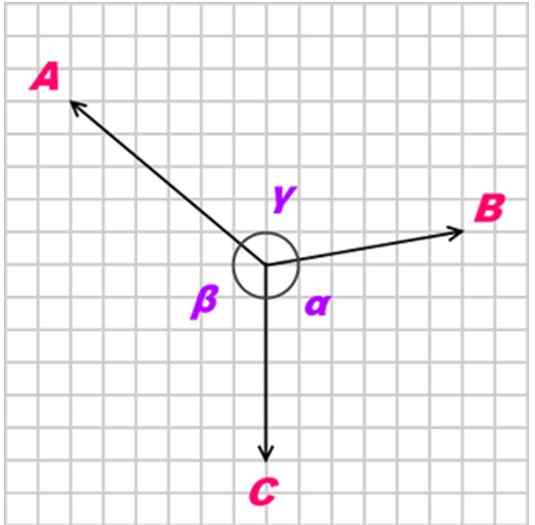Obrázok 3. Lamyho veta sa vzťahuje na súbežné a koplanárne sily. Zdroj: Wikimedia Commons.

Vyriešené cvičenia

-Cvičenie 1

V tabuľke síl na obrázku 2 váži 225 g (modré napätie) a 150 g (červené napätie) sú zavesené, s zobrazenými uhlami. Nájdite hodnotu vyrovnávacej sily a uhol, ktorý tento tvar zvislou osou.

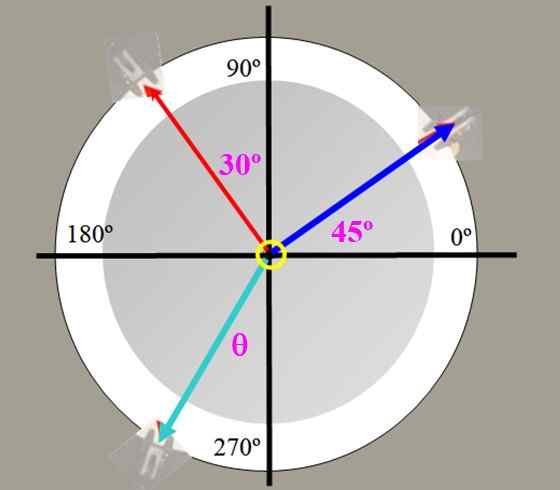Obrázok 4. Tabuľka síl na cvičenie 1.

Riešenie

Problém je možné vyriešiť s váhami vyjadrenými v gramoch (sily). Nechať p₁ = 150 gramov a p₂ = 225 gramov, príslušné zložky každého z nich sú:

P_1x = 225 . cos 45 ° g = 159.10 g; P_1y = 225 . cos 45 ° g = 159.10 g

P_2x = -150 . Sen 30 ° g = -75.00 g; P_{2 a} = 150 . Cos 30 ° g = 129.90 g

Výsledná hmotnosť P_R Komponenty sa algebraicky pridávajú:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Rytmus = 159.10 + 129.90 g = 289.00 g

Vyvažovanie váhy P_A je opačný vektor P_R:

P_Bývalý = -84.10 g

P_Hej = -289.00 g

Rozsah vyrovnávacej hmotnosti sa počíta:

P_A = (P_Bývalý² + P_Hej²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

Uhol 9 obrázku je:

9 = arctg (-84.10 / -289.00) = 16.2. vzhľadom na os a negatívny.

-Cvičenie 2

Nájdite vyrovnávací vektor systému zobrazený na obrázku, s vedomím, že každý štvorcový meria 10 m strany.

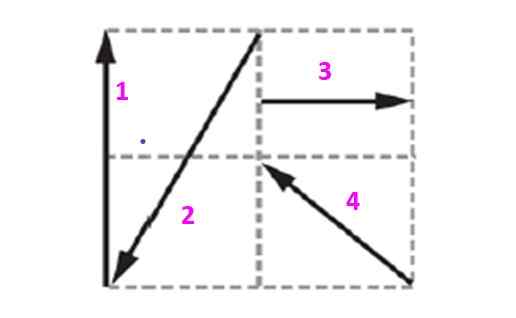Obrázok 5. Diagram pre príklad vyriešený 2.

Riešenie

Vektory obsiahnuté v tejto mriežke budú vyjadrené z hľadiska jednotky a ortogonálnych vektorov Jo a J ktoré určujú rovinu. Vektor 1, ktorý bude označený ako vložka₁ Má veľkosť 20 m a je nasmerovaný vertikálne nahor. Dá sa vyjadriť ako:

Môže vám slúžiť: prenos žiarenia (s príkladmi)

vložka₁ = 0 Jo +dvadsať J m

Z výkresu je pozorované, že vektor 2 je:

vložka₂ = -10 Jo - dvadsať J m

Vektor 3 je horizontálny a body na pozitívnej adrese:

vložka₃ = 10 Jo + 0 J  m

Nakoniec je vektor 4 naklonený 45 °, pretože je to diagonál štvorca, preto jeho komponenty merajú rovnako:

vložka₄ = -10 Jo + 10 J m

Všimnite si, že značka -.

Výsledný vektor sa získa pridaním komponentového komponentu:

vložka_R = -10 Jo + 10 J m

Potom je vyvážený vektor systému:

vložka_A = 10 Jo - 10 J m

Odkazy

1. Brada, t. 2011. Úvod do vektorov. Získané z: nrich.Matematika.orgán.
2. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley. 38-52.
3. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika.31-68.
4. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
5. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť. 15-53.
6. Kalkulačka kalkulačky vektor. Získané zo: 1728.orgán
7. Vektory. Získané z: Wikibooks.orgán