Definícia Equocent Vectors, notácia, cvičenia

Dve alebo viac Vektory sú vybavenie Ak majú rovnaký modul, rovnaký smer a rovnaký zmysel, aj keď je ich bod pôvodu iný. Pamätajte, že charakteristiky vektora sú presne: pôvod, modul, smer a zmysel. 

Vektory sú reprezentované orientovaným segmentom alebo šípkou. Obrázok 1 zobrazuje znázornenie niekoľkých vektorov v rovine, z ktorých niektoré sú vybavenie podľa pôvodne uvedenej definície.

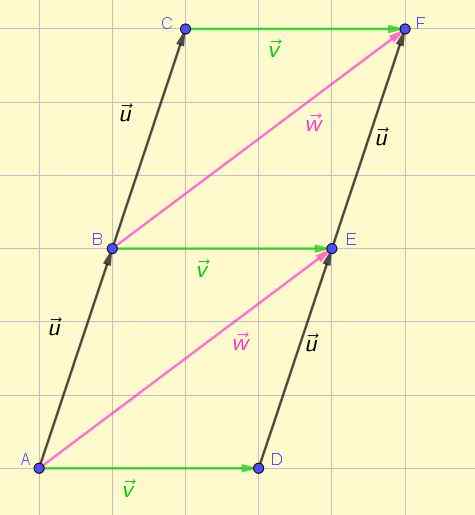postava 1. Vektory vybavenia a nevybavenia. Zdroj: Self Made.

Od prvého pohľadu je možné oceniť, že tri zelené vektory majú rovnakú veľkosť, rovnaký smer a rovnaký zmysel. To isté možno potvrdiť o dvoch ružových vektoroch a štyroch čiernych vektoroch.

Početné veľkosti prírody majú vektorové správanie, ako je prípad rýchlosti, zrýchlenia a sily, aby sme pomenovali iba niektoré. Preto je dôležitosť ich správne charakterizovania.

[TOC]

Notácia pre vektory a vybavenie

Na rozlíšenie vektorových množstiev skalárnych sumy sa často používa písmeno čierneho typu alebo šípka na písmene. Pri práci s ručnými vektormi, na notebooku, je potrebné ich rozlíšiť šípkou a keď sa používa tlačené médium, používajú sa tučné.

Vektory môžu byť odopreté, čo naznačuje ich východiskový bod alebo pôvod a bod príchodu. Napríklad AB, Bc, Z a Ef Obrázok 1 sú však vektory AB, Bc, Z a Ef Sú to skalárne množstvá alebo čísla, ktoré označujú veľkosť, modul alebo veľkosť ich príslušných vektorov.

Na označenie, že dva vektory sú vybavenie, sa používa symbol “∼ “. S týmto zápisom na obrázku môžeme poukázať na tieto vektory, ktoré sú navzájom vybavené:

Môže vám slúžiť: Kinetická energia: Charakteristiky, typy, príklady, cvičenia

AB + BC +DE -EEF 

Všetci majú rovnakú veľkosť, smer a význam. Preto dodržiavajú vyššie uvedené nariadenia.

Zadarmo, posuvné a protiľahlé vektory

Ktorýkoľvek z vektorov na obrázku (napríklad AB) je predstaviteľom súboru všetkých pevných vektorov. Táto nekonečná sada definuje triedu voľných vektorov alebo.

alebo = AB, BC, od, ef, ..

Alternatívny zápis je nasledujúci:

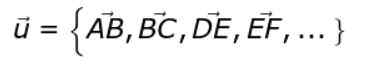
Ak tučný alebo šíp nie je umiestnený na vrchu alebo, Chceme odkazovať na vektorový modul alebo.

Bezplatné vektory sa nevzťahujú na určitý konkrétny bod.

Na ich časť Posuvné vektory Sú vybavením zariadenia pre daný vektor, ale ich aplikácia musí byť obsiahnutá vo vektorovej akčnej linke.

A oproti vektorom Sú to vektory, ktoré majú rovnakú veľkosť a smer, ale opačné zmysly, hoci v anglických textoch sa nazývajú opačné adresy Pretože adresa tiež naznačuje význam. Oproti vektorom nie sú vybavenie.

Cvičenia

-Cvičenie 1

Ktoré ďalšie vektory tých, ktoré sú znázornené na obrázku 1, sú navzájom vybavenie?

Riešenie

Okrem tých, ktoré už boli uvedené v predchádzajúcej časti, je zrejmé, že na obrázku 1 Reklama, Byť a ES Sú to tiež navzájom vybavené vektory:

AD ∼ BE ∼ CE 

Ktorýkoľvek z nich je zástupcom triedy voľných vektorov vložka.

Vektory sú tiež vybavením medzi sebou Ae a Bf :

Ae ∼ Bf 

Ktorí sú triedny zástupcovia W.

-Cvičenie 2

Body A, B a C sú na karteziánskom XY Plane a ich súradnice sú:

Môže vám slúžiť: ideálny plyn: model, správanie, príklady

A = (-4,1), b = (-1,4) a c = (-4, -3)

Nájdite súradnice štvrtého bodu D, takže vektory AB a CD Vybaviť.

Riešenie 

Tak CD vybaviť AB musí mať rovnaký modul a rovnaký smer ako AB .

Modul AB Námestie je:

|AB|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D Súradnice nie sú známe pre to, čo môžeme povedať: D = (x, y)

Potom: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Ako |AB| = |CD| Je to jedna z podmienok pre AB a CD Buďte vybavením, ktoré máte:

(x + 4)^2 + (y + 3)^2 = 18

Pretože existujú dva neznáme, je potrebná ďalšia rovnica, ktorú je možné dosiahnuť zo stavu, ktorý AB a CD byť paralelný a v rovnakom zmysle.

Vektorový sklon

Vektorový sklon AB označuje vašu adresu:

Čakanie AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Naznačujúc, že ​​vektor AB 45 ° s osou x.

CD Vektorový sklon

Sklon CD Vypočíta sa podobne:

Čakanie CD = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Zodpovedajúci tomuto výsledku s sklonom AB Máte nasledujúcu rovnicu:

Y + 3 = x + 4 

Čo znamená y = x + 1.

Ak sa tento výsledok nahradí v rovnici rovnosti modulov, je to:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Zjednodušenie je:

2 (x+4)^2 = 18, 

Čo je rovnocenné:

(x+4)^2 = 9

To je x+4 = 3, čo znamená, že x = -1. Takže súradnice D sú (-1, 0).

kontrola

Vektorové komponenty AB Sú (-1-(-4); 4 -1) = (3; 3)

Môže vám slúžiť: Théveninova veta: Čo pozostáva, aplikácie a príklady

a tie vektora CD Sú (-1-(-4)); 0 -(-3)) = (3; 3)

Čo znamená, že vektory sú vybavenie. Ak majú dva vektory rovnaké karteziánske komponenty, majú rovnaký modul a smer, preto ide o vybavenie.

-Cvičenie 3

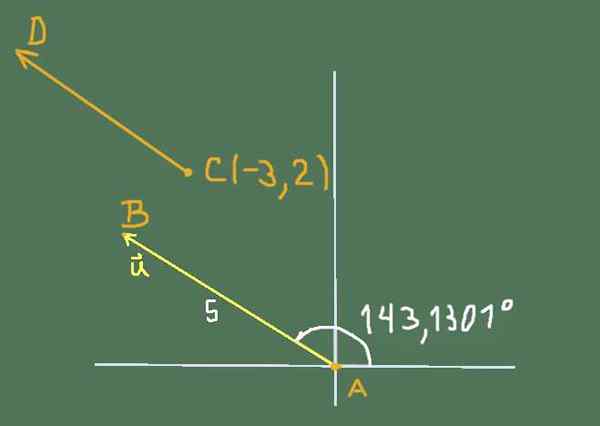
Voľný vektor alebo má veľkosť 5 a adresu 143 1301 °.

Nájdite svoje karteziánske komponenty a určte súradnice bodov B a C s vedomím, že pevné vektory AB a CD sú zariadenia. Súradnice A sú (0, 0) a súradnice bodu C sú (-3,2).

Riešenie 

Situáciu navrhnutá cvičením môže predstavovať nasledujúci obrázok:

Obrázok 2. Schéma rozlíšenia cvičenia 3. Zdroj: Self Made.

Karteziánske komponenty alebo byť

alebo = (5*cos (143 1301 °); 5*sin (143 1301 °)))))) 

Zostáva výpočty:

alebo = (-4; 3) 

B súradnice nie sú známe, takže umiestnime B (x, y)

Vektorove súradnice AB Sú (X-0; Y-0), ale keďže je to vybavenie s U, musí sa splniť rovnosť komponentov, dospelo sa preto k záveru, že súradnice B sú (-4, 3).

Podobne súradnice vektorov CD Sú (x-(-3)); (a - 2) to musí byť vybavenie u, lalebo to vedie k:

 x + 3 = -4 a y -2 = 3

Potom súradnice bodu D budú (-7, 5).

Odkazy

1. Kalkulácia.Dc. Pevný vektor. Vektor. Obnovené z: výpočtu.Dc
2. 2d Descartes. Pevné vektory a voľné vektory lietadla. Zdroj: Zdroje.vzdelávanie.je
3. Projekt guao. Vybavovacie vektory. Získané z: Guao.orgán
4. Resnick, r., Krane, K. (2001). Fyzika (v angličtine). New York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Fyzika pre vedcov a inžinierov (v angličtine) (6. vydanie). Brooks/cole.
6. Tupler, Paul a. (2000). Fyzika pre vedu a techniku. Zväzok I. Barcelona: Ed. Obrátil som sa.
7. Weisstein, e. „Vektor“. Vo Weisstein, Eric W. Mathworld (v angličtine). Výskum Wolfram.