Normálny výpočet a príklad vektora

On Normálny vektor Je to ten, ktorý definuje smer kolmo na geometrickú entitu, ktorá môže byť pre krivku, rovinu alebo povrch.

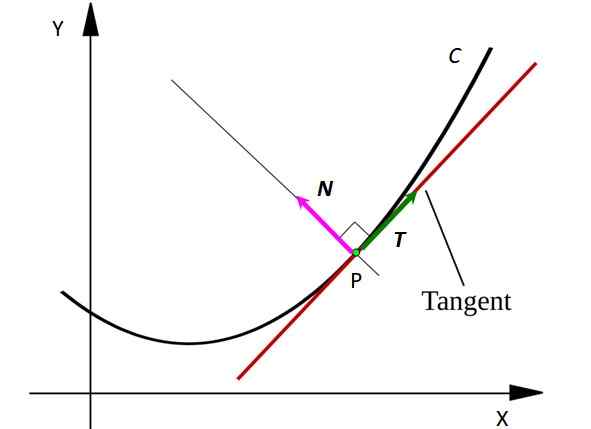
Je to veľmi užitočný koncept pri polohovaní mobilnej častice alebo nejakého povrchu vo vesmíre. V nasledujúcom grafe je možné vidieť, ako je normálny vektor na ľubovoľnú krivku C:

postava 1. Krivka C s normálnym vektorom do krivky v bode P. Zdroj: SVJO [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Zvážte bod P na krivke C. Bod môže predstavovať mobilnú častice, ktorá sa pohybuje po ceste tvare C. Čiara tangens do krivky v bode P je nakreslená červenou farbou.

Všimnite si, že vektor Tón Je dotyční k C v každom bode, zatiaľ čo vektor N je kolmo na Tón a poukazuje na stred imaginárneho obvodu, ktorého oblúk je segmentom C. Vektory sú označené tučným písmenom v tlačenom texte, aby sa odlíšili od ostatných ne -vektorových veľkostí.

Vektor Tón Vždy označuje, kam sa častice pohybujú, preto označuje rýchlosť rovnakej rýchlosti. Namiesto toho vektor N Vždy nasmerujte v smere, v ktorom sa častica otáča, týmto spôsobom naznačuje konkávnosť krivky C.

[TOC]

Ako dostať normálny vektor do lietadla?

Normálny vektor nie je nevyhnutne jednotkový vektor, to znamená vektor, ktorého modul je 1, ale ak áno, nazýva sa to normálny jednotkový vektor.

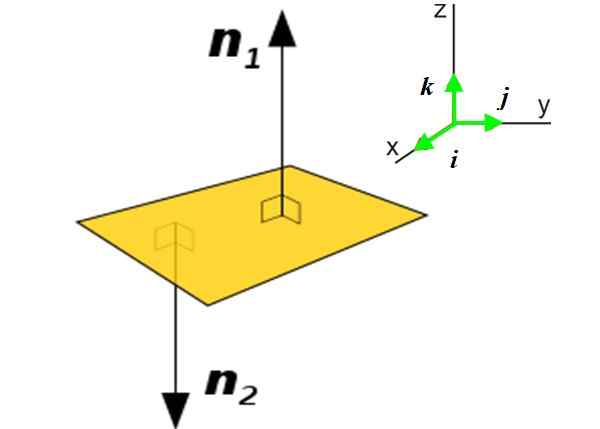
Obrázok 2. Vľavo rovina P a dva normálne vektory do uvedenej roviny. Vpravo jednotkové vektory v troch smeroch, ktoré určujú priestor. Zdroj: Wikimedia Commons. Pozri stránku Autor [Public Domain]

V mnohých aplikáciách je potrebné poznať normálny vektor do roviny namiesto krivky. Tento vektor oznámi orientáciu uvedenej roviny vo vesmíre. Zvážte napríklad lietadlo P (žltá) obrázku:

Môže vám slúžiť: Gemine: pôvod, charakteristiky a ako ich pozorovať

Do tejto roviny sú dva normálne vektory: n₁ a n₂. Použitie jedného alebo druhého bude závisieť od kontextu, v ktorom sa nachádza uvedená rovina. Získanie normálneho vektora do roviny je veľmi jednoduché, ak je jeho rovnica známa:

Ax + od + cz + d = 0, s do, b, c a d skutočné čísla.

Normálny vektor roviny je daný:

N = a Jo + b J + c klimatizovať

Tu vektor N je vyjadrený z hľadiska jednotkových vektorov a kolmo na seba Jo, J a klimatizovať, nasmerované v troch smeroch, ktoré určujú priestor X a z, Pozri obrázok 2 vpravo.

Normálny vektor z vektorového produktu

Veľmi jednoduchý postup na nájdenie normálneho vektora využíva vlastnosti vektorového produktu medzi dvoma vektormi.

Ako je známe, tri rôzne body a nie kolineal navzájom, určte rovinu P. Teraz je možné získať dva vektory alebo a vložka ktoré patria k uvedenému lietadlu s týmito tromi bodmi.

Akonáhle sú vektory, Vektorový produkt alebo X vložka Je to operácia, ktorej výsledkom je vektor, ktorý má vlastnosť kolmá na rovinu určenú podľa alebo a vložka.

Známy tento vektor, je označený ako N, A z nej bude možné určiť rovnicu roviny vďaka rovnici uvedenej v predchádzajúcej časti:

N = alebo X vložka

Nasledujúci obrázok zobrazuje opísaný postup:

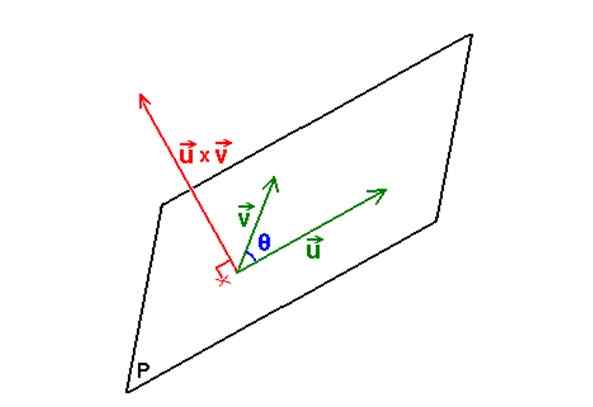Obrázok 3. S dvoma vektormi a ich vektorom alebo krížovým produktom je stanovená rovnica roviny obsahujúcej dva vektory. Zdroj: Wikimedia Commons. Nie je k dispozícii žiadny strojovo čitateľný autor. M.Romero Schmidtke predpokladal (na základe nárokov na autorské práva). [Verejná doména]

Príklad

Nájdite rovnicu roviny určenej bodmi A (2,1,3); B (0,1,1); C (4,2,1).

Môže vám slúžiť: Rovnica kontinuity

Riešenie

Toto cvičenie ilustruje vyššie opísaný postup. Tým, že má 3 body, jeden z nich je vybraný ako spoločný pôvod dvoch vektorov, ktoré patria do lietadla definovanej týmito bodmi. Napríklad bod A je nastavený ako pôvod a vektory sú postavené AB a Ac.

Vektor AB Je to vektor, ktorého pôvod je bod A a ktorého koniec je bod B. Vektorove súradnice AB Súradnice B súradníc A:

AB = (0-2) Jo + (1-1) J + (1-3) klimatizovať = -2Jo + 0J -2 klimatizovať

Postupujte rovnakým spôsobom, aby ste našli vektor Ac:

Ac = (4-2) Jo + (2-1) J + (1-3) klimatizovať = 2Jo + J -2 klimatizovať

Výpočet vektorov AB X AC

Existuje niekoľko postupov na nájdenie vektorového produktu medzi dvoma vektormi. V tomto príklade sa používa konektor Jo, J a K:

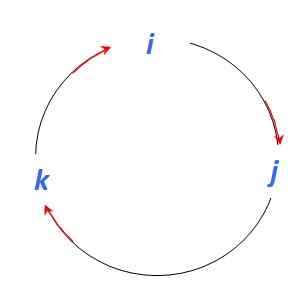Obrázok 4. Grafika na určenie vektorového produktu medzi jednotkovými vektormi. Zdroj: Self Made.

Ak chcete začať, je dobré pamätať na to, že vektorové produkty medzi paralelnými vektormi sú neplatné, preto:

Jo X Jo = 0; J X J = 0; klimatizovať X klimatizovať = 0

A keďže vektorový produkt je ďalším vektorom kolmým na zúčastnené vektory, pohybujúci sa v smere červenej šípky, ktorú máte:

Jo X J = klimatizovať ; J X klimatizovať = Jo; klimatizovať X Jo = J

Ak sa musíte pohybovať v rozpore s šípkou, pridá sa znamenie (-):

J X Jo = - klimatizovať; klimatizovať X J = -Jo; Jo X klimatizovať = -J

Celkovo je možné vyrobiť 9 vektorových výrobkov s jednotkovými vektormi Jo, J a klimatizovať, z ktorých 3 budú neplatné.

AB X Ac = (-2Jo + 0J -2 klimatizovať) X (2Jo + J -2 klimatizovať) = -4 (Jo X Jo) -2 (Jo X J) +4 (Jo X klimatizovať) +0 (J X Jo) + 0 (J X J) - 0 (J X klimatizovať) - 4 (klimatizovať X Jo) -2 (klimatizovať X J) + 4 (klimatizovať X klimatizovať) = -2klimatizovať-4J-4J+2Jo = 2Jo -8J-2klimatizovať

Rovnica lietadla

Vektor N bol stanovený predtým vypočítaným vektorovým produktom:

Môže vám slúžiť: kyvadlový pohyb

N = 2Jo -8J-2klimatizovať

Preto a = 2, b = -8, c = -2, hľadaný plán je:

Ax + od + cz + d = 0 → 2x-8y-2z + d = 0

Hodnota d. Je to ľahké, ak sú hodnoty niektorého z bodov A, B alebo C dostupné v rovnici roviny. Výber c napríklad:

x = 4; y = 2; Z = 1

Zostane:

2.4 - 8.2 - 2.1 + d = 0

-10 + d = 0

D = 10

Stručne povedané, požadovaná rovina je:

2x-8y-2z +10 = 0

Dohodný čitateľ sa môže opýtať, či by sa dosiahol rovnaký výsledok, ak namiesto toho AB X Ac Bolo by to vybrané Ac X AB. Odpoveď je áno, rovina určená týmito tromi bodmi je jedinečná a má dva normálne vektory, ako je znázornené na obrázku 2.

Pokiaľ ide o vybraný bod ako pôvod vektorov, nie je tiež nepríjemné pri výbere niektorého z ďalších dvoch.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB). 31-62.
2. Nájdenie normálu pre lietadlo. Zdroj: Web.mamička.Utexas.Edu.
3. Larson, R. (1986). Výpočet a geometria. MC Graw Hill. 616 - 647.
4. Riadky a plány v R 3. Získané z: matematiky.Harvard.Edu.
5. Normálny vektor. Obnovené z Mathworld.Valfram.com.