Fyzický

Vektorová riaditeľka Rovnica riadku, vyriešené cvičenia

Vektorová riaditeľka Rovnica riadku, vyriešené cvičenia

Rozumie to Režisér vektor Ten, kto definuje smer čiary, buď v lietadle alebo vo vesmíre. Preto sa vektor paralelne s riadkom môže považovať za jeho riaditeľa.

To je možné vďaka axiómu euklidovskej geometrie, ktorá hovorí, že dva body definujú čiaru. Potom orientovaný segment, ktorý tvorí tieto dva body.

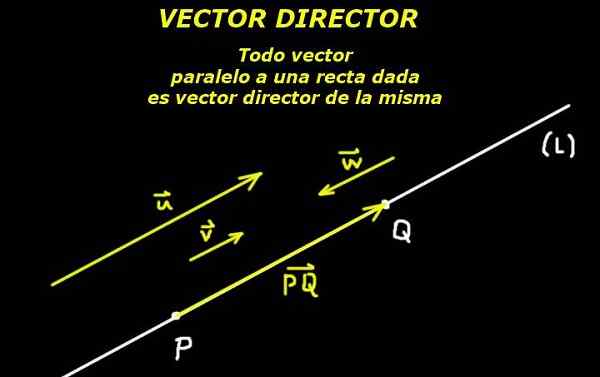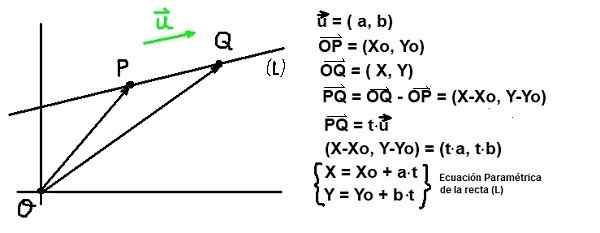
postava 1. Vektorový riaditeľ linky. (Vlastné rozpracovanie)

Daný bod P patriaci k linke (L) a daný režisérskeho vektora alebo Z tohto riadku je čiara úplne určená.

[TOC]

Rovnica riadku a riaditeľa riaditeľa

Obrázok 2. Rovnica riadku a riaditeľa riaditeľa. (Vlastné rozpracovanie)

Daný bod P koordinácií Otázka: (Xo, ja) a vektor alebo Riaditeľ linky (L), Všetky body Otázka koordinácií Otázka: (x, y) musí splniť tento vektor Pq byť paralelne s u. Táto posledná podmienka je zaručená, ak Pq Je úmerný alebo:

Pq = tlekalebo

V predchádzajúcom výraze tón Je to parameter, ktorý patrí do skutočných čísel.

Ak karteziánske komponenty Pq a alebo Predchádzajúca rovnica je napísaná takto:

(X-xo, y-yo) = tlek (a, b)

Ak sa komponenty vektorovej rovnosti rovnajú nasledujúcemu páru rovníc:

X - xo = a⋅t      a   A - ja = b⋅t 

Parametrická rovnica riadku

Súradnice X a A bodu patriaceho k línii (L) To prechádza súradnicovým bodom (Xo, ja) A je rovnobežné s Režisér vektor alebo= (a, b) Sú určené priradením skutočných hodnôt k premennému parametra T:

X = xo + a⋅t; Y = ja + b⋅t

Príklad 1

Na ilustráciu významu parametrickej rovnice riadku berieme ako režisér Vector

Môže vám slúžiť: zvlnená optika

alebo = (a, b) = (2, -1) 

a ako známy bod čiary bod 

P = (xo, me) = (1, 5). 

Parametrická rovnica riadku je:

X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞

Na ilustráciu významu tejto rovnice Obrázok 3 ukazuje, kde parameter t sa mení hodnota a bod Otázka  koordinácií (X, y) Zaujme rôzne pozície na linke.

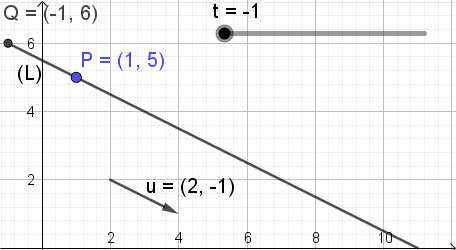Obrázok 3. Pq = t u. (Vlastné rozpracovanie)

Čiara vo vektorovej forme

Vzhľadom na bod P línie a jej riaditeľa alebo jej riaditeľ alebo rovnica linky je možné písať vo vektorovej podobe:

Oq = Oproti + λ⋅alebo 

V predchádzajúcej rovnici, ktorá je akýkoľvek bod, ale patrí do riadku a λ Skutočné číslo.

Vektorová rovnica linky je použiteľná na ľubovoľný počet rozmerov, je možné definovať aj hyper-éret.

V trojrozmernom prípade pre režisérskeho vektora alebo= (a, b, c) a bod P = (xo, ja, zo), Súradnice všeobecného bodu Q = (x, y, z) Patriace k riadku je:

(X a z) = (Xo, i, zo) + λ⋅ (a, b, c)

Príklad 2

Zoberme si znova líniu, ktorá má riaditeľa riaditeľa  

alebo = (a, b) = (2, -1) 

a ako známy bod čiary bod 

P = (xo, me) = (1, 5). 

Vektorová rovnica tohto riadku je:

(X, y) = (1, 5) + λ⋅ (2, -1) 

Nepretržitá forma línie a režisér vektor

Počnúc parametrickým formulárom, vymazaním a porovnávaním parametra λ, ktorý máte:

(X-xo)/a = (y-yo)/b = (z-zo)/c

Toto je symetrická forma riadkovej rovnice. cítim to do, b a c Sú súčasťou režiséra vektora.

Príklad 3

Zvážte líniu, ktorá má riaditeľa riaditeľa  

alebo = (a, b) = (2, -1) 

a ako známy bod čiary bod 

Môže vám slúžiť: Aká je elektrina? (S experimentom)

P = (xo, me) = (1, 5). Nájdite svoju symetrickú formu.

Symetrická alebo kontinuálna forma je na línii: je:

(X - 1)/2 = (y - 5)/( - 1)

Všeobecná forma riadkovej rovnice

Je známa ako všeobecná forma čiary v rovine XY k rovnici, ktorú má nasledujúca štruktúra:

A⋅x + b⋅y = c

Expresia symetrickej formy je možné prepísať tak, aby mala všeobecnú formu:

B⋅x - a⋅y = b⋅xo - ark

V porovnaní so všeobecnou formou riadku zostáva: 

A = b, b = -a a c = B⋅xo - a⋅o 

Príklad 3

Nájdite všeobecnú formu línie, ktorej režisér je u = (2, -1)

 A čo prechádza bodom p = (1, 5).

Na nájdenie všeobecného formulára môžeme použiť dané vzorce, ale bude zvolená alternatívna cesta.

Začneme nájdením dvojitého vektora W vektora U, ktorý je definovaný ako vektor, ktorý sa získava výmenou komponentov U a vynásobením -1 druhým:

W= (-1, -2)

Dvojitý vektor W zodpovedá rotácii v 90 ° v pláne riaditeľa riaditeľa vložka.

Zúčastňujeme sa lezenie W s (X, y) a (Xo, ja) A zhodujeme sa:

(-1, -2) • (x, y) = (-1, -2) • (1, 5)

-X -2y = -1 -22 = -11

Konečne zostávajú:

X + 2y = 11

Štandardný tvar riadkovej rovnice

Je známa ako štandardná forma čiary v rovine XY, ktorá má nasledujúcu štruktúru:

Y = m⋅x + d

kde m predstavuje sklon a odpočet D s osou a.

Vzhľadom na režisér u = (a, b) vektor, sklon m je b/a.

A D sa získava nahradením X a Y známym bodom XO, Me:

I = (b/a) xo + d.

Stručne povedané, m = b/a y d = ja -(b/a) xo

Všimnite si, že sklon m je kvocient medzi komponentom a režiséra a komponenta X to isté.

Môže vám slúžiť: Rotačná rovnováha: vzorce a rovnice, príklady, cvičenia

Príklad 4

Nájdite štandardný tvar línie, ktorého režisér je u = (2, -1) 

A čo prechádza bodom p = (1, 5).

M = -½ a d = 5 -( -½) 1 = 11/2

Y = (-1/2) x + 11/2

Vyriešené cvičenia

-Cvičenie 1

Nájdite vektorový riaditeľ riadku (L), ktorý je priesečníkom roviny (π): x - y + z = 3 a rovina (Ω): 2x + y = 1.

Potom napíšte kontinuálnu formu riadku riadku (L).

Riešenie

Z rovnice roviny (Ω) vôľa y: y = 1 -2x

Potom nahradíme rovnicu roviny (π):

X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x

Potom parametrizujeme x, vyberieme parametrizáciu x = λ

To znamená, že riadok má vektorovú rovnicu danú:

(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)

to možno prepísať ako:

(X, y, z) = (0, 1, 4) + λ (1, -2, -3)

S tým, čo je jasné, že vektor alebo = (1, -2, -3) je priamy riadiaci vektor (l).

Kontinuálna forma čiary (L) je:

(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)

-Cvičenie 2

Vzhľadom na 5x rovinu + do Y + 4z = 5 

a riadok, ktorej rovnica je x/1 = (y-2)/3 = (z -2)/(-2)

Určiť hodnotu do takže rovina a čiara sú rovnobežné.

Riešenie 2

Vektor n = (5, a, 4) je normálny vektor do roviny.

Vektor alebo = (1, 3, -2) je priamy manažér.

Ak je čiara rovnobežná s rovinou, potom n • v = 0.

(5, do, 4)•(1, 3, -2) = 5 +3do -8 = 0 ⇒ do= 1.

Odkazy

  1. Fleming, w., & Varberg, D. A. (1989). Matematika. Prentice Hall PTR.
  2. Kolman, B. (2006). Lineárna algebra. Pearson Vzdelanie.
  3. Lojálny, j. M., & Viloria, n. G. (2005). Plochá analytická geometria. Mérida - Venezuela: Venezuelský redaktor C. Do.
  4. Navarro, Rocio. Vektory. Získané z: Knihy.Riadenie.co.ísť.
  5. Pérez, C. D. (2006). Predkválka. Pearson Vzdelanie.
  6. Prenowitz, w. 2012. Základné koncepty geometrie. Rowman a Littlefield.
  7. Sullivan, m. (1997). Predkválka. Pearson Vzdelanie.