Vektory vo vesmíre Ako graf, aplikácie, cvičenia

A vektor vo vesmíre Je to všetko zastúpené súradnicovým systémom, ktorý dal X, a a z. Takmer vždy lietadlo Xy Je to rovina vodorovného povrchu a osi z predstavuje výšku (alebo hĺbku).

Karteziánske súradnicové osi znázornené na obrázku 1, rozdeľujú priestor do 8 oblastí nazývaných Oktavery, analogické s tým, ako osi X - a Rozdeľte lietadlo na 4 kvadranty. Potom budeme mať 1 oktant, 2. Ocanto a tak ďalej.

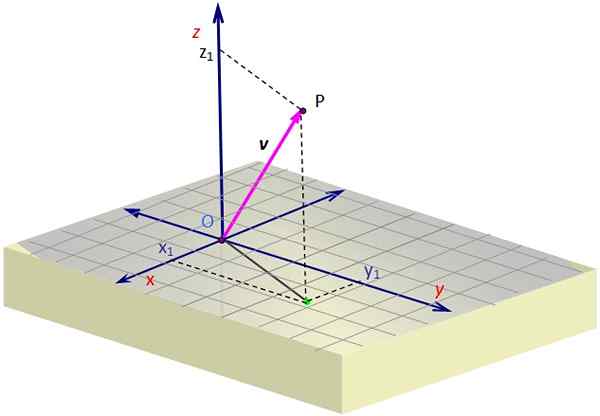
postava 1. Vektor vo vesmíre. Zdroj: Self Made.

Obrázok 1 obsahuje znázornenie vektora vložka v priestore. Na vytvorenie ilúzie troch rozmerov na rovine obrazovky je potrebná určitá perspektíva.

Ak chcete grafovať 3D vektor, musíte pomôcť bodkovaným čiar, ktoré určujú súradnice projekcie alebo „tieňa“ mriežky vložka Nad povrchom x---. Táto projekcia sa začína v O a končí v zelenom bode.

Akonáhle tam musíte pokračovať vertikálnou výškou (alebo hĺbkou) potrebnou podľa hodnoty z, kým sa nedostanete k P. Vektor je čerpaný z O a končiaci v p, ktorý je v príklade v 1. príhode.

[TOC]

Žiadosti

Vektory vo vesmíre sa široko používajú v mechanike a iných vetviach fyziky a inžinierstva, pretože štruktúry, ktoré nás obklopujú, vyžadujú geometriu v troch rozmeroch.

Pozičné vektory vo vesmíre sa používajú na umiestnenie objektov vzhľadom na referenčný bod nazývaný pôvod Ani. Preto sú tiež potrebnými nástrojmi v navigácii, ale to nie je všetko.

Môže vám slúžiť: Elektromagnetické vlny: Maxwell Teória, typy, charakteristiky

Sily pôsobiace na štruktúry, ako sú skrutky, podpery, káble, vzpery a ďalšie sú vektorová povaha a sú orientované vo vesmíre. Aby ste poznali jeho účinok, je potrebné poznať vašu adresu (a tiež váš bod aplikácie).

A často smer sily je známy dvoma bodmi vo vesmíre, ktoré patria do jej línie akcie. Týmto spôsobom je sila:

F = F alebo

Kde f je veľkosť alebo modul sily a alebo Je to jednotkový vektor (modul 1) nasmerovaný pozdĺž riadku pôsobenia F. 

3D vektorový zápis a reprezentácie

Pred vyriešením niektorých príkladov sa v stručne prehodnotí zápis 3D vektorov.

V príklade na obrázku 1, vektor V, ktorého bod pôvodu sa zhoduje s pôvodom alebo a ktorého koniec je bod P, má súradnice X a z Pozitívne, zatiaľ čo koordinujte a Je to negatívne. Tieto súradnice sú: X₁, a₁, z₁, ktoré sú presne súradnicami P.

Takže ak máme vektor spojený s pôvodom, tj, ktorého východiskový bod sa zhoduje s O, je veľmi ľahké označiť jeho súradnice, ktoré budú extrémne body alebo P. Aby sme rozlíšili medzi bodom a vektorom, použijeme pre najnovšie výrazné písmená a zátvorky, ako je tento:

vložka = < x₁, a₁, z₁ >

Zatiaľ čo bod P je označený zátvorkami:

P = (x₁, a₁, z₁)

Ďalšia reprezentácia využíva jednotkové vektory Jo, J a klimatizovať ktoré definujú tri smery priestoru v osi X, a a z respektíve.

Tieto vektory sú navzájom kolmé a tvoria Ortonormálna základňa (Pozri obrázok 2). To znamená, že 3D vektor môže byť napísaný z hľadiska nich ako:

Môže vám slúžiť: zvlnený pohyb: charakteristiky, typy vĺn, príklady

vložka = v_X Jo + vložka_a J + vložka_z klimatizovať

Uhly a Cosenos riaditelia vektora

Obrázok 2 tiež zobrazuje uhly režisérov γ₁, γ₂ a γ₃ ako vektor vložka respektíve osi X, a a z. Poznanie týchto uhlov a veľkosť vektora je to úplne určené. Okrem toho kosíny riaditeľov spĺňajú nasledujúci vzťah:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

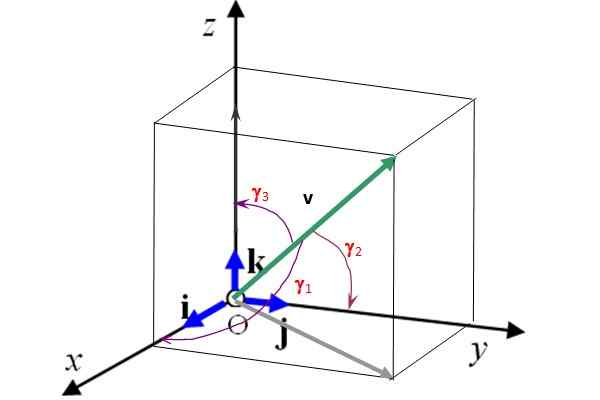Obrázok 2. Unitárne vektory i, j a k určujú 3 preferenčné smery priestoru. Zdroj: Self Made.

Vyriešené cvičenia

-Cvičenie 1

Na obrázku 2 uhly y₁, γ₂ a γ₃ ako vektor vložka formy modulu 50 s súradnicovými osami sú: 75.0 °, 60.0 ° a 34.Tretí. Nájdite karteziánske komponenty tohto vektora a reprezentujte ho z hľadiska jednotkových vektorov Jo, J a klimatizovať.

Riešenie

Projekcia vektora vložka na osi X je v_X = 50 . Cos 75 ° = 12.941. Podobne projekcia vložka na osi a je v_a = 50 cos 60 ° = 25 a nakoniec na osi z je v_z = 50. cos 34.3. = 41.3. Teraz vložka možno vyjadriť ako:

vložka = 12.9 Jo + 25.0 J + 41.3 klimatizovať

-Cvičenie 2 

Nájdite napätie v každom z káblov, ktoré držia vedro obrázku, ktorý je v rovnováhe, ak je to hmotnosť 30 n.

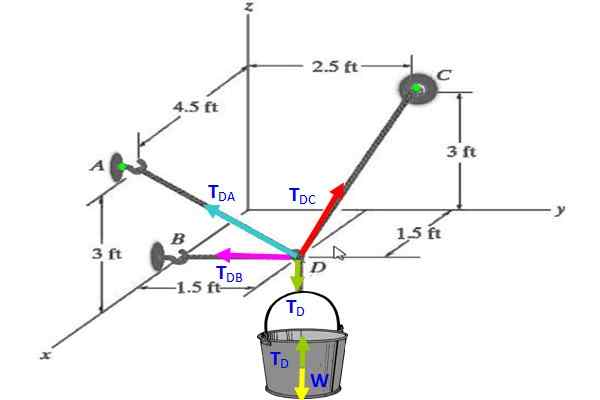Obrázok 3. Schéma napätia pre cvičenie 2.

Riešenie

Na vedre, diagram voľného tela naznačuje, že to naznačuje Tón_D (zelená) kompenzuje hmotnosť W (žltá), preto t_D = W = 30 n.

V uzle vektor Tón_D  Je nasmerovaný vertikálne nadol, potom:

Tón_D = 30 (-klimatizovať) N.

Ak chcete stanoviť zostávajúce napätie, musíte postupovať podľa nasledujúcich krokov:

Krok 1: Nájdite súradnice všetkých bodov

A = (4.5; 0; 3) (A je na stene lietadla X-Z)

B = (1.5; 0; 0) (B je na osi x)

Môže vám slúžiť: Adresa (fyzická)

C = (0, 2.5, 3) (C je v stene lietadla a z)

D = (1.5; 1.5; 0) (D je na horizontálnej rovine  x---)

Krok 2: Nájdite vektory v každom smere odpočítaním súradníc konca a začiatku

Dávať =

Dc =

Db =

Krok 3: Vypočítajte moduly a jednotkové vektory

Jednotkový vektor sa získa výrazom: alebo = r / r, s r .

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

alebo_Dávať = 4.5 =

alebo_Dc = 3.5 =

alebo_Db =

alebo_D =

Krok 4: Vyjadrite všetky napätia ako vektory

Tón_Dávať = T_Dávať alebo_Dávať = T_Dávať

Tón_Dc = T_Dc alebo_{Dc =}  Tón_Dc

Tón_Db = T_Db alebo_Db = T_Db

 Tón_D = 30

Krok 5: Použite statickú rovnovážnu podmienku a vyriešte systém rovníc

Nakoniec sa na vedro aplikuje statická rovnováha, takže vektorový súčet všetkých síl na uzle je neplatný:

Tón_Dávať + Tón_Dc + Tón_Db + Tón_D = 0

Keďže napätie je vo vesmíre, povedie k systému troch rovníc pre každú komponent (X, a a a z) napätie.

0.67 t_Dávať -0.43 t_Dc + 0 t_Db = 0

-0.33 t_Dávať + 0.29 t_Dc - Tón_Db = 0

0.67 t_Dávať + 0.86 t_Dc +0 t_Db - 30 = 0

Riešenie je: T_Dávať = 14.9 n; Tón_Dávať = 23.3 n; Tón_Db = 1.82 n

Odkazy

1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley. 38-52.
2. Figueroa, D. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika.31-68.
3. Fyzický. Modul 8: Vektory. Získané z: FRTL.Utn.Edu.ar
4. Hibbeler, R. 2006. Mechanika pre inžinierov. Statický. 6. vydanie. Kontinentálna redakčná spoločnosť. 15-53.
5. Kalkulačka kalkulačky vektor. Získané zo: 1728.orgán