Absolútna hodnota

Aká je absolútna hodnota?

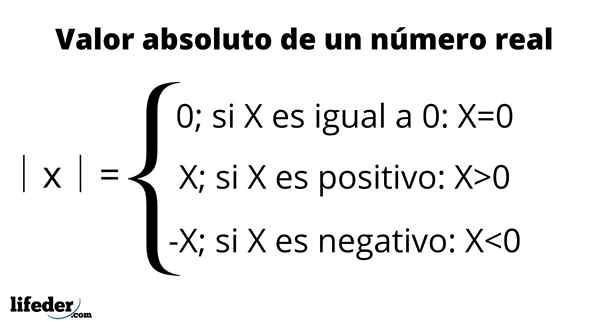
On absolútna hodnota skutočného čísla je definovaná ako vzdialenosť medzi týmto číslom a 0 skutočnej čiary. Za to, že je vzdialenosť, je jej hodnota vždy kladná alebo nula a rovná sa číslu.

Absolútna hodnota je znázornená umiestnením čísla medzi dva vertikálne pruhy, symbol, ktorý sa číta: “absolútna hodnota“, Ako je zhrnuté v nasledujúcej tabuľke:

Napríklad absolútna hodnota -3 je napísaná ako │ -3│ a je rovná 3. To znamená, že medzi -3 a 0 existujú tri jednotky, ktoré predstavujú čísla na reálnom riadku. Na druhej strane, absolútna hodnota +3 alebo jednoducho 3 sa tiež rovná 3, pretože meraním jej vzdialenosti na 0 je to tiež tri jednotky.

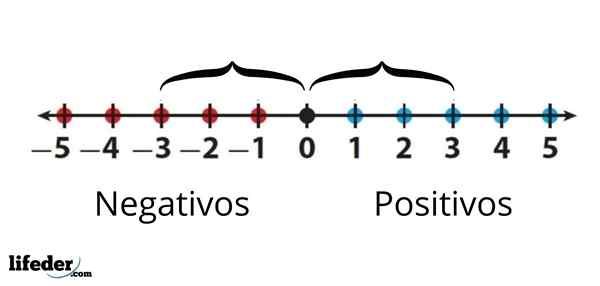Absolútna hodnota -3 sa rovná absolútnej hodnote +3, pretože vzdialenosť medzi buď medzi 0 je rovnaká

Stručne povedané, absolútna hodnota čísla je rovnaká hodnota čísla, ale vždy s kladným znakom.

Vlastnosti absolútnej hodnoty

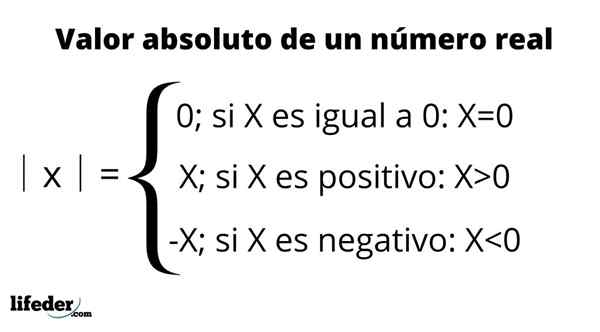Definícia absolútnej hodnoty

Hlavné vlastnosti absolútnej hodnoty:

• 1) Absolútna hodnota čísla je vždy kladná alebo 0, preto:

│x│≥ 0

• 2) Absolútna hodnota nuly je tiež nula, to znamená │0│ = 0, preto je možné potvrdiť, že:

│x│ = 0, áno y, iba ak x = 0

• 3) Pre každé číslo X, ktoré patrí do množiny reálnych čísel, sa absolútna hodnota x rovná absolútnej hodnote - x:

│x│ = │ - x│

• 4) Ak je absolútna hodnota čísla X A, znamená to, že pre toto číslo existujú dve možnosti: i) x = +a alebo ii) x = -a.

Môže vám slúžiť: Mary cestuje 2/4 cyklistov, Melissa Travels 4/8 a Anahi cestuje 3/6

Napríklad, ak je absolútna hodnota čísla 5, dve možnosti sú, že číslo je +5 alebo -5.

Operácie s absolútnou hodnotou

Nasledujúce vlastnosti sú veľmi užitočné na vykonávanie operácií s absolútnymi hodnotami:

• 5) Pre „x“ a „y“, ktoré sú dve skutočné čísla, je vždy splnená nasledujúca nerovnosť, ktorá sa nazýva nazvaná trojuholníková nerovnosť absolútnej hodnoty:

│x│+│y│≥ │x+y│

Napríklad:

x = -6

y = 9

Ľavá strana nerovnosti je:

│-6│ + │9│ = 6 + 9 = 16

A pravá strana je:

│-6+9│ = │3│ = 3

Je zrejmé, že 16 je väčšie alebo rovná 3, a to vždy v prípade, keď čísla x a majú rôzne príznaky. Ak majú rovnaké príznaky, získa sa rovnosť. Pozri tento ďalší príklad s dvoma ďalšími rôznymi hodnotami:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Naozaj:

8 = 8

• 6) Produkt príslušných absolútnych hodnôt dvoch skutočných čísel „x“ a „y“ sa rovná absolútnej hodnote produktu čísel:

│x│ ∙ │y│ = │x ∙ y│

Opäť sú hodnoty:

x = -6

y = 9

Tak:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Čo sa rovná:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Kvocient absolútnej hodnoty dvoch reálnych čísel „X“ a „Y“, s rôznym menovateľom 0, je absolútnou hodnotou kvocientu medzi týmito číslami:

Pokiaľ a ≠ 0.

Príklad:

Príklady absolútnej hodnoty

Jednoduché príklady

Výpočet absolútnej hodnoty akéhokoľvek skutočného čísla je veľmi jednoduchý, napríklad absolútna hodnota nasledujúcich čísel je:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Výpočty s absolútnou hodnotou skutočného čísla

Vykonajte nasledujúce operácie, ktoré zahŕňajú absolútnu hodnotu:

a) 2lek8 │ + 5lek -16│ -dre 4│ = (2 šverici) + (5q16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Môže vám slúžiť: polovica z 15

Toto je kombinovaná operácia, takže je lepšie ju vyriešiť podľa krokov. Prvá absolútna hodnota je:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Druhá absolútna hodnota, ktorá sa objaví, sa vypočíta takto:

│81 ÷ (-3) │ = │-27│ = 27

Potom sa získajú získané výsledky a uskutoční sa konečný výpočet:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Vzdialenosť medzi dvoma bodmi na skutočnej čiare

Absolútna hodnota sa objavuje v mnohých aplikáciách, napríklad nájdenie vzdialenosti medzi dvoma číslami, ktoré patria do skutočnej čiary. Ak je A skutočné číslo, potom sa nachádza na skutočnom riadku v bode, ktorého Abscissa je „A“, to isté sa deje so skutočným číslom B.

Nechajte „A“ a „B“ dve čísla na skutočnej čiare, vzdialenosť, ktorá ich oddeľuje, je:

d_AB = │b - a│

Ktoré je možné vypočítať aj podľa:

d_AB = │a - b│

Napríklad vzdialenosť medzi a = 5 a b = 12 je:

D = │5-12│ = │12-5│ = 7

Týmto spôsobom je absolútna hodnota odčítania medzi dvoma reálnymi číslami jednoducho vzdialenosť, ktorá ich oddeľuje na skutočnej čiare.

Funkcia absolútnej hodnoty

Funkcia absolútnej hodnoty je aplikácia, ktorá prebieha v množine reálnych čísel ℛ do ℛ⁺, čo zodpovedá každému skutočnému číslu jeho absolútnu hodnotu. Je definovaný:

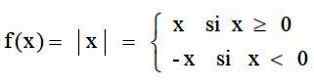
A jeho graf má typickú formu V:

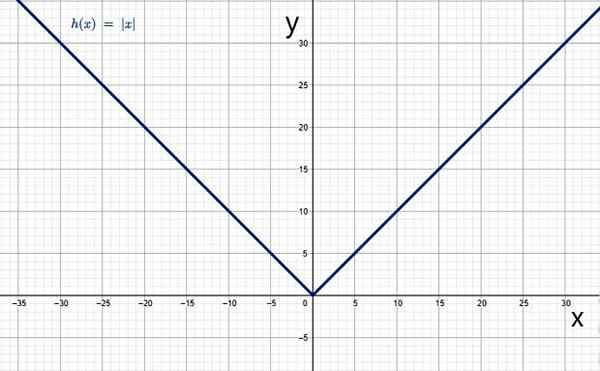Absolútna hodnota ako funkcia. Zdroj: f. Zapata cez geogebra.

Charakteristiky funkcie absolútnej hodnoty

-Vaša doména je sada všetkých skutočných čísel.

-Je to nepretržité.

-Je dokonca, pretože je splnené, že f (x) = f (-x), preto vertikálna os je os symetrie.

-Rozsah funkcie absolútnej hodnoty je sada pozitívnych reálnych, vrátane 0, pretože funkcia vždy predstavuje vzdialenosť, a to je vždy pozitívne alebo nulové.

Môže vám slúžiť: čo je usmernenie? (Geometria)

-Je to funkcia podľa sekcií alebo častí.

-Pokles v intervale (-∞, 0) a rastie v (0,+∞).

Argument absolútnej hodnoty môže byť tiež kvadratickou alebo inou funkciou, je možné ho definovať:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

Absolútna hodnota je zodpovedná za to, že sa stane pozitívnymi obrázkami argumentu, ktoré majú negatívny znak.

Vyriešené cvičenia

Cvičenie 1

Vyhodnoťte nasledujúce algebraické výrazy s absolútnou hodnotou:

a) │2x -5│ + │ -x + 1│ pri x = 3

b) │ (x - 5) ÷ (x+4) │ pri x = −1

Roztok

│2⋅3-5│ + │ - 3 + 1│ = │6-5│ + │ - 2│ = │1│ + 2 = 3

Riešenie B

│ (−1-5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Cvičenie 2

Aká je sada hodnôt, ktorá predstavuje nasledujúcu nerovnosť?

│X│ <3

Riešenie

Nerovnosť predstavuje všetky reálne čísla, ktorých absolútna hodnota je nižšia alebo rovná 3, preto je to sada všetkých čísel medzi -3 a +3, vrátane týchto.

V intervalovom zápise zostáva:

[-3,3]

Cvičenie 3

Vyriešte nasledujúcu rovnicu s absolútnou hodnotou:

│2x-1│ = 5

Riešenie 

Ako už bolo uvedené, na vyriešenie rovnice s absolútnou hodnotou je potrebné zvážiť tieto dve možnosti. Myslím že áno:

│f (x) │ = c

Tak:

1) f (x) = c

2) f (x) = -c

Preto táto rovnica, ktorej argument je lineárny, má dve riešenia:

Prvé riešenie

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Druhé riešenie

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Pri hodnotení x₁ = 3 alebo x₂ = -2 V pôvodnej rovnici sa musí získať rovnosť, týmto spôsobom sa overuje, že získané hodnoty sú riešením navrhovanej rovnice. Naozaj:

│ (2⋅3) -1│ = │6-1│ = 5

A keď sa snažíte s druhou možnosťou, získa sa aj rovnosť:

│2lek (-2) -1│ = │-4-1│ = 5

Odkazy

1. Baldor, a. 2005. Algebra. Kultúrna vlastná skupina.
2. Larson, R. 2012. Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
3. Hoffman, J. Výber matematických problémov. Zväzok 2.
4. Stewart, J. 2007. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.