Perfektný štvorcový trinomén

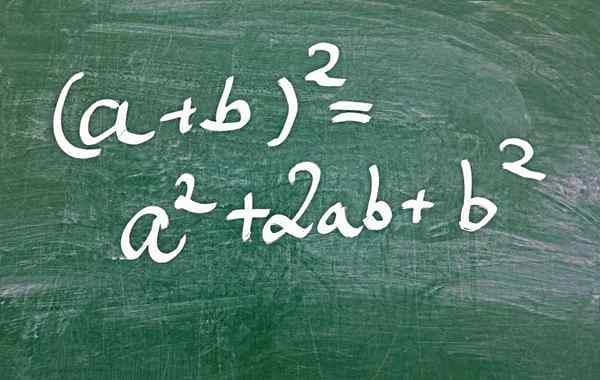postava 1.- Jedným zo spôsobov, ako získať dokonalý štvorcový trinomén, je cez štvorec sumy

Čo je perfektný štvorcový trinomiál?

Perfektný štvorcový trinomický je to, že polynóm troch termínov, z ktorých dva sú perfektné štvorce sumy A a B a predchádzajú rovnaké znamenie, zatiaľ čo tretí termín je presne dvojitým produktom A a B, ktorý je schopný byť iné znamenie.

Perfektný štvorcový trinomial sa získava štvorcovým súčtom alebo rozdielom binomického a algebraicky, jeho tvar je nasledujúci:

do² ± 2 ∙ AB + B²

Ako je vidieť, perfektný štvorcový trinomén obsahuje:

• Dva nevýznamné kvadratické výrazy, ktorému predchádzali rovnaké znamenie: a² a b²
• Tretí termín 2 ∙ AB, ktorý je dvojitým produktom odmocniny kvadratických výrazov a ktorému môže predchádzať pozitívnym alebo negatívnym znakom.

Perfect Square Trinomials môžu byť jeden alebo viac variabilných. Napríklad nasledujúci trinomial je dokonalým štvorcom premennej:

• X² + 6x + 9

Všimnite si, že prvé výrazy (x²) a tretí (9) sú štvorcové sumy nazývané A a B. Naozaj, x² Je to štvorec X a 9 je štvorec 3. Týmto spôsobom môžete napísať nasledujúce:

a = x

B = 3

A zostávajúci termín je dvojitým produktom X a 3:

6x = 2 ∙ 3 ​​∙ x

Po vykonaní overenia je isté, že tento trinomial je perfektný štvorec.

Príklady

Obrázok 2.- Príklady dokonalých štvorcových trinomialov. Zdroj: f. Zapata.

Perfect Square Trinomials sa tiež objavujú napríklad v dvoch alebo viacerých premenných:

4x² + 4xy + a²

Je to trinomial v dvoch premenných: „x“ a „y“. Môže sa ubezpečiť, že ide o dokonalý štvorcový trinomén, pretože predstavuje dva kvadratické pojmy:

4x² = (2x)²

a² = (y)²

A zostávajúci termín je dvojitým produktom príslušných druhých odmocniny: „2x“ a „y“:

Môže vám slúžiť: ortoedro: vzorce, oblasť, objem, diagonálne, príklady

4xy = 2 ∙ 2x ∙ a

Trinomialy prezentované doteraz sú stupňom 2 v premennej „x“, ale nemusia byť nevyhnutne také. Nasledujúca trinomial je stupeň 4 v „X“:

9x⁴ - 30x²YZ + 25Y²z²

Ľahko sa overuje, že ide o perfektný štvorcový trinomén. Prvý termín je perfektný 3x štvorcový², Odvtedy (3x²)² = 9x⁴.

Termín 25 rokov²z² sa rovná (5yz)². Nakoniec zostávajúci termín je 2 ∙ 3x²∙ 5yz = 30 x²a z.

Na druhej strane, trinomialy uvedené nižšie nie sú dokonalé štvorcové trinomialy:

• X²  + 8x - 16

Nie je to dokonalý štvorcový trinomiálny, pretože 16, hoci je to 4², Predchádza mu negatívny znak, zatiaľ čo druhý kvadratický termín (x²) je pozitívny.

• X²  - 15x + 25

Nie je to ani dokonalý štvorcový trinomiál, pretože hoci má dva kvadratické pojmy: x² a 5², Termín 15x sa nerovná 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Tento trinomén nie je dokonalým štvorcom, pretože obsahuje iba kvadratický termín: 4x² = (2x)².

Štvorcový súčet a štvorcový rozdiel

Perfect Square Trinomials sa získavajú vývojom dvoch typov pozoruhodných výrobkov:

• Štvorec sumy.
• Štvorec rozdielu.

Najprv sa vývoj získa z distribučnej vlastnosti, pretože zvyšovanie štvorcových binomiálnych znamená, že sa mu vynásobí samotný:

(A ± b)² = (a ± b) × (a ± b) = a² ± A ∙ B ± b ∙ a + b² = a² ± 2A ∙ B + B²

Získané trinomiálne je výsledok, ktorý sa zapamätal iba s trochou praxe a je to druh skratky, ktorý uľahčuje vývoj, a preto sa nazýva pozoruhodný produkt.

Môže vám slúžiť: Transcendentné čísla: čo sú, vzorce, príklady, cvičenia

Nasledujúce trinomialy sa dajú ľahko získať pomocou pozoruhodného produktu bez toho, aby sa zvýšila distribučná vlastnosť.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 a² +20xy + 4x²

Faktorizácia dokonalého štvorcového trinomialu

Častá a nevyhnutná prevádzka v algebre je faktorizácia dokonalého štvorcového trinomialu, prostredníctvom ktorého je trinomiál vyjadrený ako štvorec súčtu alebo odčítanie dvoch výrazov (binomický).

Je to opačná operácia, ktorá vyvíja významný produkt, pretože má výsledný trinomén, ide o získanie binomiálu, ktorý mu vyvoláva, keď stúpne na 2.

Napríklad v predtým analyzovanom 4x perfektnom štvorcovom trinomícii² + 4xy + a², Čo je binomial, že keď je na druhú, vedie vám?

Príslušné druhé korene kvadratických pojmov sú:

√ (4x²) = 2x

Čo je rovnocenné: 4x² = (2x)²

√ (a²) = y

Rovnocenné s tým, že to hovorí: a² = (y)²

Preto:

4x² + 4xy + a² = (2x + y)²

A čo je binomiál, ktorý pochádza z perfektného štvorcového trinomialu 9x⁴ - 30x²YZ + 25Y²z²? Opäť sa extrahujú druhé korene kvadratických pojmov:

√ (9x⁴) = 3x²

√ (25 a²z²) = 5yz

Tak:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25Y²z²

Vyriešené cvičenia

Cvičenie 1

V každom z nasledujúcich trinomialov vyplňte prázdne miesto s pojmom, ktorý chýba, aby bol perfektným štvorcovým trinomiálom:

a) m² + 18 m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Roztok

Podľa vzorca pozoruhodného produktu:

Môže vám slúžiť: doplnkové uhly: ktoré a ako sa vypočítajú, príklady, cvičenia

(A ± b)² = A² ± 2A ∙ B + B²

Trinomialu:

m² + 18 m + _____

Z toho vyplýva:

a = m (tak² = m²)

Okrem toho centrálny termín je: 2 ∙ a ∙ b = 2m ∙ b = 18 m, preto b = 9 a jeho štvorec je 9² = 81. Guy podľa vzorca pozoruhodného produktu, trinomial je taký:

(M + 9)² = M² + 18 m + 81

• Riešenie B

V tomto trinomiáli:

4x² - _____ + 64

Môžete vedieť a b:

A = √ (4x²) = 2x

B = √64 = 8

Chýbajúci termín je preto dvojitým produktom A a B:

2 ∙ ab = 2 ∙ 8 ∙ 2x = 32x

A vyhľadávaný trinomén je:

4x² - 32x + 64

• Riešenie c

V trinomiálnom:

_____ + 30n + 25

Prvý termín chýba, ale je známe, že:

B = √25 = 5

A

2 ∙ ab = 2 ∙ a ∙ 5 = 10a = 30n

Preto A = 3N a vyhľadávané trinomiálne je:

9n² + 30n + 25

Cvičenie 2

Skontrolujte, či je ďalším perfektným štvorcovým trinomiálnym a faktorom je:

16 rokov² - 24yz + 9z²

• Riešenie

Najprv je dokázané, že k kvadratickým pojmom predchádza rovnaké znamenie a potom sa nájdu príslušné druhé korene:

A = √ (16 rokov²) = 4y

B = √ (9z²) = 3z

Potom musíte overiť, či zostávajúci výraz je dvojitým produktom A a B:

2 ∙ ab = 2 ∙ 4y ∙ 3z = 24yz

Ak je, potom trinomiál môže byť faktorom ako štvorec rozdielu, pretože ústrednému termínu predchádza negatívny znak:

16 rokov² - 24yz + 9z² = (4y - 3z)²

Odkazy

1. Jiménez, r. 2008. Algebra. Sála.
2. Matematické hodiny Kate. Perfektné štvorcové trinomialy. Získané z: Katesmathlessons.com.
3. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
4. Zill, D. 2008. Predbežné náskoky s výpočtovými pokrokmi. 4. Vydanie. McGraw Hill.