Trajektória a posun

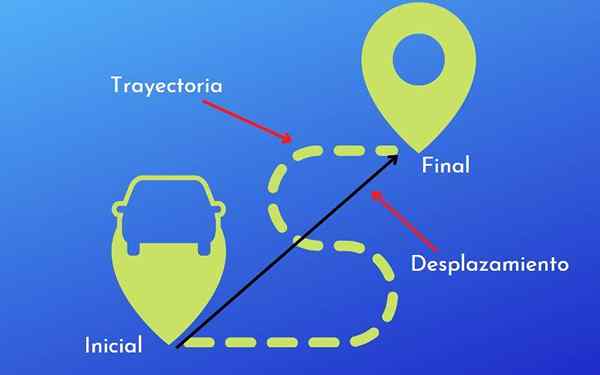
Rozdiel medzi trajektóriou a posunom. S licenciou

Ten Rozdiel medzi trajektóriou a posunom je, že druhá je vzdialenosť a smer, ktorý sa pohybuje objektom, zatiaľ čo trajektóriou je cesta alebo forma prijatá pohybom tohto objektu.

Avšak, aby sme videli jasnejšie rozdiely medzi posunom a trajektóriom, je lepšie vysvetliť príklady, ktoré umožňujú väčšie pochopenie oboch výrazov.

Posunutie

Je chápaná ako vzdialenosť a smer, ktorý sa pohybuje objektom, berúc do úvahy jeho počiatočnú polohu a jeho konečnú polohu, vždy v priamke. Na jeho výpočet, pretože ide o veľkosť vektora, sa používajú merania dĺžky známe ako centimetre, metre alebo kilometre.

Vzorec na výpočet posunu je definovaný takto:

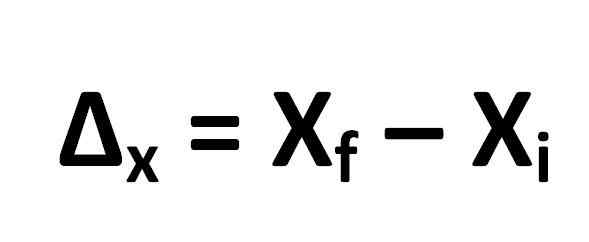
Z čoho to nasleduje:

- Δ_X = posun

- X_F = konečná poloha objektu

- X_Jo = Počiatočná poloha objektu

Príklad posunu

1. Ak je skupina detí na začiatku trasy, ktorej počiatočná poloha je 50 m, ktorá sa pohybuje v priamke a určuje posun v každom z bodov x_F. 

- X_F = 120 m

- X_F = 90 m

- X_F = 60 m

- X_F = 40 m

2. Problémové údaje sa extrahujú nahradením hodnôt x₂ a x₁ Vo vzorci posunu:

- Δ_X = ?

- X_Jo = 50 m

- Δ_X = X_F - X_Jo

- Δ_X = 120 m - 50 m = 70 m

3. V tomto prvom prístupe hovoríme, že δ_X Sa rovná 120 m, čo zodpovedá prvej hodnote, ktorú nájdeme od x_F, Menej 50 m, čo je hodnota x_Jo, Výsledkom je 70 m, to znamená, že keď dosiahlo 120 m, posunutie bolo 70 m doprava.

Môže vám slúžiť: Laboratórna vetva

4. Pokračujeme v riešení rovnakým spôsobom pre hodnoty B, C a D

- Δ_X = 90 m - 50 m = 40 m

- Δ_X = 60 m - 50 m = 10 m

- Δ_X = 40 m - 50 m = - 10 m

V tomto prípade nám vysídlenie dalo negatívne, to znamená, že konečná poloha je v opačnom smere počiatočnej polohy.

Trajektória

Je to trasa alebo čiara určená objektom počas jeho pohybu a hodnotenia v medzinárodnom systéme, vo všeobecnosti prijíma geometrické tvary, ako je čiara, podobenstvo, kruh alebo elipsa.

Je identifikovaný prostredníctvom imaginárnej čiary a tým, že je skalárnym množstvom, ktoré sa meria v metroch.

Je potrebné poznamenať, že na výpočet trajektórie musíme vedieť, či je telo v pokoji alebo sa pohybuje, to znamená, že sa predkladá do referenčného systému, ktorý vyberieme.

Rovnica na výpočet trajektórie objektu v medzinárodnom systéme je daná:

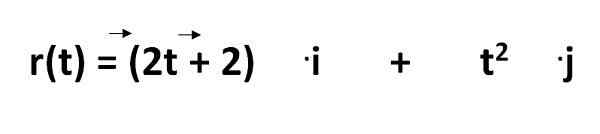
Z ktorých musíme:

- R (t) = je to rovnica trajektórie

- 2T - 2 a t² = reprezentovať súradnice ako funkcia času

-  ^.Ja a ^.J = sú jednotkové vektory

Aby sme pochopili výpočet trajektórie prevezenej objektom, vyvinieme nasledujúci príklad:

Vypočítajte rovnicu trajektórií nasledujúcich vektorov polohy:

- R (t) = (2t + 7) ^.i + t^{2 .}J

- R (t) = (t - 2) ^.Výstup ^.J

Prvý krok: ako rovnica trajektórie je funkciou X, aby to definovalo hodnoty x a y v každom zvýšenom vektoroch:

1. Vyriešiť vektor prvej polohy:

- R (t) = (2T + 7) ^.i + t^{2 .}J

2. Ty = f (x), kde x je daný obsahom vektora jednotky ^.I e a je daný obsahom vektora jednotky ^.J:

Môže vám slúžiť: ad hoc: pôvod pojmu, významy a príklady použitia

- X = 2t + 7

- Y = t²

3. y = f (x), to znamená, že čas nie je súčasťou výrazu, preto ho musíme vyčistiť, máme:

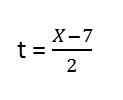
4. Vymeníme výbavu v a. Pobyty:

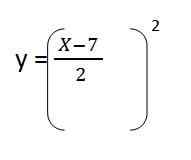
5. Vyriešime obsah zátvorky a máme rovnicu výslednej trajektórie pre prvý vektor jednotky:

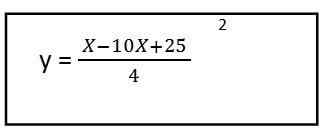
Ako vidíme, vyústilo do rovnice druhého stupňa, to znamená, že trajektória je pre tvar paraboly.

Druhý krok: Pokračujeme rovnakým spôsobom pre výpočet trajektórie druhého vektora jednotky:

1. R (t) = (t - 2) ^.Výstup ^.J

- X = t - 2

- Y = 2t

2. Podľa krokov, ktoré sme predtým videli y = f (x), musíme vyčistiť čas, pretože nie je súčasťou výrazu, máme:

- t = x + 2

3. Vymeníme povolenie v a zostaneme:

- y = 2 (x + 2)

4. Vyriešenie zátvorky máme rovnicu výslednej trajektórie pre druhý vektor jednotky:

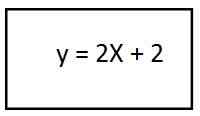
V tomto postupe sme vyústili do riadku, ktorá nám hovorí, že trajektória má priamu formulár.

Pochopili koncepty vysídlenia a trajektórie, môžeme odvodiť zvyšky rozdielov, ktoré existujú medzi oboma výrazmi.

Viac rozdielov medzi posunom a trajektóriom

Posunutie

- Je to vzdialenosť a smer, ktorý sa pohybuje objektom, berúc do úvahy jeho počiatočnú polohu a jeho konečnú polohu.

- Vždy sa stáva v priamke.

- Je rozpoznávaný šípkou.

- Použite opatrenia dĺžky (centimeter, meter, kilometer).

- Je to vektorová suma.

- Berte do úvahy smerovaný smer (vpravo alebo vľavo)

- Nezohľadňuje čas strávený počas prehliadky.

Môže vám slúžiť: kondenzácia: koncept, proces, príklady

- Nezávisí to od referenčného systému.

- Ak je východiskový bod rovnaký východiskový bod, posun je nula.

- Modul sa musí zhodovať s priestorom, ktorý sa má cestovať, pokiaľ je trajektória priamkou a nedochádza k zmenám v zmysle nasledovať.

- Modul má tendenciu zvyšovať sa alebo znižovať pohyb, berúc do úvahy trajektóriu.

Trajektória

Je to trasa alebo čiara určená objektom počas jeho pohybu. Adoptovať geometrické tvary (rovné, parabolické, kruhové alebo eliptické).

- Je zastúpený prostredníctvom imaginárnej línie.

- Meria sa v metroch.

- Je to skalárne množstvo.

- Nezohľadňuje spôsob, akým cestoval.

- Zvážte čas strávený počas prehliadky.

- Závisí to od referenčného systému.

- Ak je počiatočný bod alebo počiatočná poloha rovnaká ako konečná poloha, trajektória je daná prejdenou vzdialenosťou.

- Hodnota trajektórie sa zhoduje s modulom posunu vektora, ak je výsledná trajektória priamkou, ale v zmysle nasledovania nie sú žiadne zmeny.

- Vždy sa zvyšuje, keď sa telo pohybuje, bez ohľadu na trajektóriu.

Odkazy

1. Fernández, m., Fidalgo, J. (2016). Fyzika a chémia 1. bakalár. Paraninfo Editions, S.Do. Španielsko.
2. Guatemalský inštitút rádiového vzdelávania (2011) Základná fyzika. Skupina Zaculeu v prvom semestri. Guatemala.