Vodorovné snímacie funkcie, vzorce a rovnice, cvičenia

On Horizontálna streľba Je to spustenie projektilu s horizontálnou rýchlosťou z určitej výšky a ponechané na pôsobenie gravitácie. Bez ohľadu na odpor vzduchu bude mať trajektória opísaná mobilom tvar oblúka paraboly.

Premietacie objekty horizontálne sú celkom bežné. Projektily sú hodené so všetkými druhmi koncov: od kameňov, s ktorými boli priehrady sklamané na začiatku príbehu, k tým, ktoré sa vykonávajú v loptových športoch a sú podrobne za sebou davy ľudí.

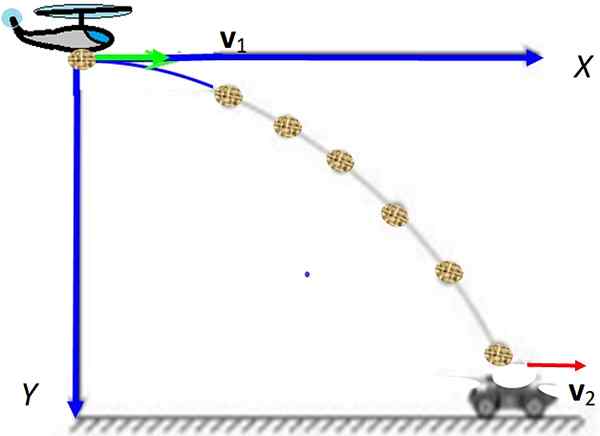
postava 1. Horizontálne snímanie s červenou rýchlosťou komponentmi. Všimnite si, že horizontálna zložka zostáva konštantná, zatiaľ čo vertikálna zložka rastie. Zdroj: Wikimedia Commons.

[TOC]

Charakteristika

Hlavné charakteristiky horizontálneho streľby sú:

-Počiatočná rýchlosť poskytnutá projektilu je kolmá na gravitáciu.

-Pohyb sa odohráva v lietadle, takže sú potrebné dve súradnice: X a a.

-Robí sa z určitej výšky H nad úrovňou zeme.

-Čas, ktorý projektil vydrží vo vzduchu, sa volá čas letu.

-Faktory, ako je odpor vzduchu alebo kolísanie, sa nezohľadňujú v hodnote g.

-Tvar, veľkosť a hmotnosť projektilu neovplyvňujú jeho pohyb.

-Pohyb sa rozkladá na dva simultánne pohyby: jeden zvislý dole pod činnosťou g; Druhý, horizontálny, s konštantnou rýchlosťou.

Vzorce a rovnice

Kinematické rovnice pre horizontálne spustenie sa získavajú z rovníc na voľný pád a rovnosti rovnomerného priameho pohybu.

Môže vám slúžiť: vnútorná energia

Ako sa jasne zobrazuje animácia na obrázku 1, projektil je vybavený horizontálnou počiatočnou rýchlosťou označenou ako ako vložka_ani = v_vôl Jo (Odvážny v tlačenom texte naznačuje, že ide o vektor).

Je poznamenané, že počiatočná rýchlosť má veľkosť vložka_vôl a je nasmerovaný pozdĺž osi X, Aký je smer vektora jednotky Jo. V animácii je tiež varované, že počiatočná rýchlosť nemá vertikálnu komponent, ale ako klesá, táto komponent sa zvyšuje rovnomerne vďaka činnosti g, zrýchlenie gravitácie.

Pokiaľ ide o horizontálnu zložku rýchlosti, zostáva konštantná, zatiaľ čo pohyb trvá.

Podľa toho, čo už bolo povedané, sú polohy stanovené ako funkcia času, a to na horizontálnej osi aj vo vertikálnej osi. Právo sa berie ako os +x, zatiaľ čo dole je adresa -a. Hodnota gravitácie je G = -9.8 m/s² ani -32 stôp/s²:

x (t) = x_ani + vložka_vôl.t (horizontálna poloha); vložka_vôl Je to konštantné

a (t) = y_ani + vložka_Odvoz.T - ½ g.tón² (vertikálna poloha); vložka_a = v_Odvoz - g.T (vertikálna rýchlosť)

Poloha, rýchlosť, čas letu a maximálny horizontálny rozsah

Rovnice sú zjednodušené, ak si vyberú nasledujúce počiatočné pozície: X_ani = 0, a_ani = 0 na mieste spustenia. Okrem vložka_Odvoz = 0, Pretože mobil je premietaný vodorovne. S touto voľbou sú rovnice pohybu také:

x (t) = v_vôl.t; vložka_X = v_vôl

a (t) = - ½ g.tón²; vložka_a = - g.tón

Ak nie je k dispozícii čas, je užitočná rovnica, ktorá sa týka rýchlosti a posunov. Toto platí pre vertikálnu rýchlosť, pretože vodorovná zostáva v celom pohybe konštantná:

Môže vám slúžiť: fluorid vápenatý (CAF2): Štruktúra, vlastnosti, používa

vložka_a² = v_Odvoz² + 2.g .y = 2.g.a

Čas letu

Na výpočet Čas letu t_let, Predpokladajme, že mobil je premietaný z výšky H na podlahe. Ako bol vybraný pôvod referenčného systému v štartovom bode, keď dosiahne zem, je v polohe -H. Nahradenie v rovnici 2) získa sa:

-H = - ½ g.tón²_let

tón_let = (2h/g)^½

Maximálny rozsah

On Horizontálny dosah Tento čas sa získa nahradením x (t):

X_Maximálny = v_vôl. (2h/g)^½

Vyriešené cvičenia

-Cvičenie vyriešené 1

Vrtuľník letí horizontálne a udržiava konštantnú výšku 580 m, keď uvoľní krabicu obsahujúcu jedlo na utečeneckom tábore. Box pristane v horizontálnej vzdialenosti 150 m od bodu jeho štartu. Nájdite: a) Čas letu v krabici.

b) rýchlosť vrtuľníka.

c) Ako rýchlo sa dotkla škatuľka?

Riešenie

a) Výška H, ​​z ktorej sa jedlo uvoľňuje, je h = 500 m. S týmito údajmi pri výmene získate:

tón_let = (2h/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) Vrtuľník nesie horizontálnu počiatočnú rýchlosť vložka_vôl balíka a keďže jedna z údajov je X_maximálny:

X_Maximálny = v_vôl. (2h/g)^½ ® vložka_vôl = x_Maximálny /(2h/g)^½= x_Maximálny / t_let = 150 m/ 10.9 s = 13.8 m/s

c) Rýchlosť projektilu v každom okamihu je:

vložka_a = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/h

Negatívny znak naznačuje, že mobilný mobilný význam sa pohybuje smerom nadol.

-Cvičenie vyriešené 2

Z lietadla, ktorá letí vodorovne vo výške H = 500 m a 200 km/h Balíček padá, ktorý musí spadnúť na otvorené vozidlo, ktoré pochoduje do 18 km/h na ceste. V ktorej polohe by malo lietadlo nechať balík spadnúť do vozidla? Nezohľadnite odpor vzduchu alebo rýchlosť vetra.

Môže vám slúžiť: rozmerová analýzaObrázok 2. Schéma pre cvičenie vyriešené 2. Zdroj: Pripravený F. Zapata.

Riešenie

Je vhodné najskôr odovzdať všetky jednotky do medzinárodného systému:

18 km/h = 6 m/s

200 km /h = 55 m /s

Existujú dva mobily: rovina (1) a vozidlo (2) a je potrebné zvoliť súradnicový systém na ich lokalizáciu oboch. Je vhodné to urobiť na východiskovom bode balenia v lietadle. Balík sa premieta horizontálne s rýchlosťou, ktorú lietadlo nesie: vložka₁, zatiaľ čo vozidlo sa pohybuje do vložka₂ domnelý konštantný.

-Lietadlo

Počiatočná poloha: x = 0; y = 0

Počiatočná rýchlosť = vložka₁ (vodorovné)

Polohové rovnice: a (t) = -½g.tón²  ; x (t) = v₁.tón

-Vozidlo

Počiatočná poloha: x = 0, y = -h

Počiatočná rýchlosť = vložka₂  (konštanta)

x (t) = x_ani + vložka₂. tón

Čas, ktorý trvá letenie balíkom, je:

tón_let = (2h/g)^½ = (2 × 500/9.8)^½S = 10.1 s

V súčasnosti balík zažil vodorovné posunutie:

X_Maximálny = v_vôl . (2h/g)^½= 55 m/s x 10.1 s = 556 m.

V súčasnosti sa vozidlo tiež pohybovalo vodorovne:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Ak lietadlo uvoľní balík okamžite, že vozidlo vidí prechod pod ňou, nebude schopné do neho spadnúť priamo. Aby sa to stalo, musí to hodiť späť:

D = 556 m - 60.6 m = 495.4 m.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 74-84.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).117 - 164.
3. Projektil. Získané z: Phys.Librettexts.orgán.
4. Rex, a. 2011. Základy fyziky. Pearson. 53-58.
5. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. McGraw Hill. 126-131.