Systém metód riešenia rovníc, príklady, cvičenia

Ten ekulačné systémy Pozostávajú z dvoch alebo viacerých rovníc s niekoľkými premennými, ktoré musia mať spoločné riešenie. Sú časté, pretože v praxi existuje veľa situácií, ktoré závisia od mnohých faktorov, ktoré súvisia niekoľkými spôsobmi.

Systém rovníc má vo všeobecnosti nasledujúcu formu, kde každá funkcia predstavuje jednu z podmienok, ktoré riešenie musí spĺňať:

postava 1. Systém rovníc pozostáva z M funkcií a n neznámy. Zdroj: f. Zapata.

Pozrime sa na príklad: Predpokladajme, že musíte vyrábať obdĺžnikové papierové listy, ktorých oblasť je 180 cm² a mať obvod 54 cm. Aké by mali byť rozmery hárku?

Aby sme odpovedali na otázku, ktorú berieme do úvahy, že rozmery obdĺžnikového hárku sú dve: široké a vysoké. To znamená, že máme 2 premenné, na ktoré dáme obvyklé mená X a a.

A tieto premenné musia spĺňať dve podmienky uložené zároveň:

-Prvá podmienka: Oblasť laminy je 180 cm². Toto bude prvá funkcia: f₁.

-Druhá podmienka: Obvod alebo obrys listu musia byť 54 cm. Toto je druhá funkcia F₂.

Pre každú podmienku sa rovnica stanoví pomocou algebraického jazyka. Oblasť A obdĺžnikového hárku sa získa vynásobením širokého:

A = x.y = 180 cm²

A obvod P vyplýva z pridávania strán. Pretože obvod je súčet strán:

P = 2x + 2y = 54 cm

Systém vyplývajúci z dvoch rovníc a dvoch neznámych je:

Xy = 180

2 (x + y) = 54

Potrebujeme dve čísla, ktorých produkt je 180 a že dvojitý produkt jeho súčtu je 54 alebo čo je rovnaké: pridané musí dať 27. Tieto čísla sú 12 a 15.

V sekcii vyriešených cvičení ponúkneme podrobnú metódu na nájdenie týchto hodnôt, zatiaľ čo čitateľ môže ľahko overiť nahradenie, čo účinne spĺňa obe rovnice.

[TOC]

Príklady aplikácií systémov rovníc

Vyššie uvedená situácia obsahuje 2 premenné a na ich nájdenie sú potrebné najmenej 2 rovnice. Existujú systémy s mnohými ďalšími premennými, ale v každom prípade, ak má systém n Z toho sa vyžaduje aspoň n Nezávislé rovnice (jedna nemôže byť lineárnou kombináciou ostatných), aby našla riešenie, ak existuje.

Môže vám slúžiť: lano (geometria): dĺžka, veta a cvičenia

Pokiaľ ide o aplikácie, sú početné. Tu sú niektoré, v ktorých systémy rovníc preukazujú svoju užitočnosť:

-Nájdite prúdy, ktoré cirkulujú cez okruh prostredníctvom Kirchoffových zákonov.

-V pozemkovej a leteckej doprave na stanovenie plánov výstupu a príchodu.

-Nájdite veľkosti síl v dynamických alebo statických systémoch podliehajúcich viacnásobným interakciám.

-Poznať množstvo položiek predávaných na určité časové obdobie alebo v továrňach, aby sa určili rozmery objektov, ktoré spĺňajú určité podmienky z hľadiska povrchu alebo objemu.

-Pri určovaní, ako rozdeliť kapitál v niekoľkých investíciách.

-Stanoviť sadzby pre rôzne služby, napríklad telekomunikácie alebo predstavenia a poznať množstvo získaných peňazí (pozri príklad vyriešený 2)

Metódy riešenia rovníc systémov

Metóda výmena

-Je vybraná rovnica a jedna z premenných je vyčistená.

-Potom musíte vymeniť jasnú premennú v inej rovnici. Potom táto premenná zmizne odtiaľ a ak má systém dve rovnice a dve neznáme, existuje rovnica s premennou, ktorá už môže byť jasná.

-Ak má systém viac ako dve premenné, musíte vyčistiť tretinu neznáme z inej rovnice a nahradiť ho tiež.

Príklad uplatňovania tejto metódy je v roku vyriešený 1.

Metóda redukcie alebo eliminácie

Táto metóda spočíva v pridávaní alebo odpočítaní rovníc na odstránenie jednej alebo viacerých premenných a zanechanie jednej. Za týmto účelom je vhodné vynásobiť rovnice faktorom tak, že pridaním s inou rovnicou neznáme zmizne. Pozrime sa na príklad:

3x² - a² = 11

Môže vám slúžiť: Ústredné opatrenia tendencie pre zoskupené údaje: vzorce, cvičenia

X² + 4y² = 8

Vynásobíme prvú rovnicu 4:

12x² - 4y² = 44

X² + 4y² = 8

Pridaním neznámeho zmiznutia a, zostať:

13x² = 52

X² = 4

Preto x₁ = 2 a x₂ = -2. S týmito hodnotami to čitateľ môže overiť a₁ = 1 a₂ = -1

Spôsob vyrovnávania

Ak je systém dve rovnice s dvoma neznámymi:

-Neznámy je vybraný a čistí obe rovnice.

-Výsledky sú vyrovnané, čo umožňuje získať jednu rovnicu s jediným neznámym.

-Táto rovnica je vyriešená a výsledok sa nahradí v jednom z predchádzajúcich zúčtovaní, aby sa získala hodnota druhého neznámeho.

Táto metóda sa použije v roku vyriešená 2 z nasledujúcej časti.

Grafická metóda

Táto metóda pozostáva z grafu kriviek, ktoré predstavuje každá rovnica. Bod križovatky je systémové riešenie. Nasledujúci príklad ukazuje grafické riešenie systému:

X² + a ² = 1

2x + 4y = 0

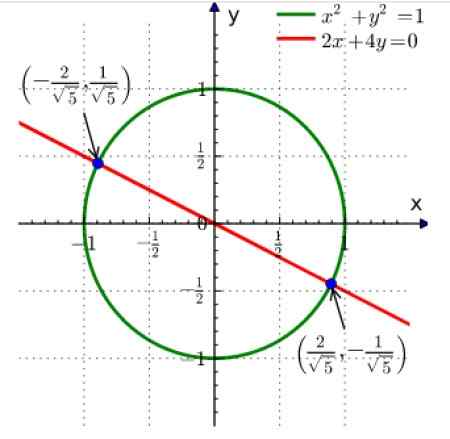Obrázok 2. Grafické riešenie systému simultánnych rovníc je nájsť priesečník kriviek. Zdroj: Wikimedia Commons.

Prvá z rovníc je kruh polomeru 1 zameraný na pôvod a druhá je čiara.

Križovatka oboch sú dva body zobrazené modrou farbou. Čitateľ môže overiť, že nahradením súradníc bod vo vyššie uvedených rovniciach sa získa rovnosť.

Cvičenia

- Cvičenie vyriešené 1

Musíte vyrábať obdĺžnikové listy v oblasti 180 cm² a s obvodom 54 cm. Aké by mali byť rozmery hárku?

Riešenie

Systém, ktorý sa má vyriešiť, je:

Xy = 180

2 (x + y) = 54

Druhá rovnica je možné zjednodušiť na x + y = 27, preto:

Xy = 180

x + y = 27

Jeden z neznámych druhej rovnice je vyčistený:

y = 27 - x

Výbava je vymenená v prvom:

(27 -x) = 180

Uplatňovanie distribučnej vlastnosti:

-X² + 27x = 180

Vynásobenie (-1) na oboch stranách rovnice a vysielaním 180 na ľavú stranu:

X² - 27x +180 = 0

Je to rovnica druhého stupňa v X, ktorá je vyriešená vzorcom:

Môže vám slúžiť: opačné uhly pri vrchole (s vyriešeným cvičením)

S a = 1, b = -27 a c = 180

 Riešenia sú: x₁ = 15 cm a x₂ = 12, preto rozmery y sú a₁ = 12 cm a a₂ = 15 cm.

- Cvičenie vyriešené 2

Zábavný park má nasledujúce sadzby na vstup: Deti 1.5 a dospelí 4 doláre. V jeden deň bolo 2200 návštevníkov, ktorí získali 5050 dolárov. Nájdite počet detí a dospelých, ktorí v ten deň navštívili park.

Obrázok 3. Systém rovníc slúži na rozdelenie zbierky zábavného parku za deň. Zdroj: Pixabay.

Riešenie

Byť X Počet detí a a Počet dospelých. Môžeme stanoviť prvú z rovníc s vedomím, že súčet oboch musí byť 2200:

x + y = 2200.

Teraz ideme s získanými peniazmi. Cena lístka pre deti je 1.5 $ pre každé dieťa vynásobením tejto hodnoty X, počtom detí, budeme mať sumu na vstup do dieťaťa:

1.5x = peniaze získané vstupenkami pre deti

A ak vynásobíme 4 doláre na dospelého za množstvo a návštevníkov dospelých, celkové peniaze získajú všetci dospelí:

4y = peniaze získané lístkami pre dospelých

Pridáme to, aby sme získali 5050 dolárov:

1.5x + 4y = 5050

Náš systém rovníc je:

x + y = 2200

1.5x + 4y = 5050

Vyriešime to vyrovnaním. Vyčistíme premennú a prvú a druhú rovnicu:

y = 2200 - x

y = (5050 - 1.5 x) /4

Rovnáme obidva výrazy:

2200 - x = (5050 - 1.5x) /4

Vynásobíme všetko 4, aby sme odstránili zlomok:

8800 - 4x = 5050 - 1.5x

Zoskupujeme výrazy s X vľavo a čisté čísla vpravo:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 detí.

Túto hodnotu nahrádzame na y = 2200 - x, aby sme poznali počet dospelých:

y = 2200 - 1500 = 700 dospelých.

Odkazy

1. CK-12. Systémy rovníc a nerovností. Získané z: CK12.orgán.
2. Hoffman, J. Výber matematických problémov. Zväzok 2.
3. Jiménez, r. 2008. Algebra. Sála.
4. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.