Koncepcia, aplikácie a príklady rovnováhy

Ten rovnováha Sú potrebné, aby telo zostalo v pokoji alebo v rovnomernom priamom pohybe. V prvom prípade sa hovorí, že objekt je v statickej rovnováhe, zatiaľ čo v druhom je v dynamickej rovnováhe.

Za predpokladu, že mobilný objekt je časticou, v takom prípade sa rozmery nezohľadňujú, stačí, že súčet síl pôsobiacich na ňu je zrušený.

postava 1. Brimhamove skaly severne od Anglicka spĺňajú rovnovážné podmienky. Zdroj: verejné domény.slepo.

Veľká väčšina mobilných objektov však má značné rozmery, preto táto podmienka nestačí na zaručenie rovnováhy, čo v každom prípade nie je absencia zrýchlenia, nie pohybu.

[TOC]

Prvá a druhá rovnovážna podmienka

Pozrime sa: Ak je súčet síl neplatný, je pravda, že objekt sa nebude rýchlo pohybovať alebo nepohybovať, ale stále by sa mohol začať otáčať.

Preto, aby sa predišlo rotáciám, musí druhá podmienka.

Krátke označovanie ako F Sieťová sila a τ ani M Na sieťový krútiaci moment budeme mať:

Podmienka prvého vyváženia

∑ F = 0

Čo znamená, že: ∑ f_X = 0, ∑ f_a = 0 a ∑ f_z = 0

Druhá rovnovážna podmienka

∑ τ = 0 alebo ∑ M = 0

S krútiacimi momentmi alebo momentmi vypočítanými s ohľadom na akýkoľvek bod.

V nasledujúcom texte budeme predpokladať, že mobilný objekt je tuhé telo, ktoré nezažije žiadnu deformáciu.

Žiadosti

Aj keď sa zdá, že hnutie je spoločným menovateľom vo vesmíre, rovnováha je prítomná aj v mnohých aspektoch prírody a v objektoch, ktoré nás obklopujú.

Môže vám slúžiť: Millikan Experiment: Postup, vysvetlenie, dôležitosť

Izostatická rovnováha

Na planétovej stupnici je Zem v izostatická rovnováha, Druh gravitačnej rovnováhy zemskej kôry, ktorej hustota nie je jednotná.

Rozdiely v hustotách rôznych blokov alebo oblastí zemskej kôry sú kompenzované výškovými rozdielmi, ktoré charakterizujú orografiu planéty. Funguje to rovnakým spôsobom, ako rôzne materiály ponoria viac -menej vo vode podľa ich hustoty a dosahujú rovnováhu.

Ale keďže bloky kôry neplávajú vo vode, ale v plášti, ktorý je oveľa viskóznejší, rovnováha sa nenazýva hydrostatická, ale izostatická.

Fúzna operácia v jadre

V hviezdach, ako je naše slnko, rovnováha medzi gravitáciou, ktorá ich komprimuje, a hydrostatický tlak, ktorý ich rozširuje, udržuje fúzny reaktor do prevádzky v jadre hviezdy, ktorá ho udržuje nažive. Závisíme od tejto rovnováhy, aby Zem prijíma potrebné svetlo a teplo.

Výstavba

V miestnom meradle chceme, aby budovy a konštrukcie zostali stabilné, to znamená, že rovnovážne podmienky dodržiavajú, najmä statickú rovnováhu.

Z tohto dôvodu vznikla statika, ktorá je odvetvím mechaniky venovanej štúdiu rovnováhy tela a všetkého, čo je potrebné na ich udržanie takto.

Typy statickej rovnováhy

V praxi zistíme, že statická rovnováha môže byť z troch tried:

Stabilná rovnováha

Vyskytuje sa, keď sa objekt presunie z jeho polohy a okamžite sa k nemu vráti, keď ju sila, ktorá ju presunula,. Čím bližšie je predmet pôdy, tým je pravdepodobnejšie, že je potrebné byť v stabilnej rovnováhe.

Môže vám slúžiť: Zjavná hustota: vzorec, jednotky a cvičenia vyriešené

Pravá guľa na obrázku 2 je dobrým príkladom, ak ju vyberieme z polohy rovnováhy na spodku misky, gravitácia bude zodpovedná za rýchle návrat.

Ľahostajná alebo neutrálna rovnováha

Vyskytuje sa, keď objekt, napriek tomu, že sa pohybuje, pokračuje v rovnováhe. Okrúhle predmety, ako je guľa, keď sú umiestnené na plochých povrchoch, sú v ľahostajnej rovnováhe.

Nestabilná rovnováha

Vyskytuje sa, keď sa objekt pohybuje z rovnovážnej polohy, nevracia sa k nemu. Ak držiame loptu pred vrcholom kopca vľavo, je isté, že sa nevráti svojimi vlastnými prostriedkami.

Obrázok 2. Rovnováha. Zdroj: Wikimedia Commons.

Príklad: častice statické

Predpokladajme blok hmoty m Na naklonenej rovine, ktorá sa má sústrediť vo svojom geometrickom centre.

Horizontálna zložka hmotnosti w_X Má tendenciu skĺznuť blok, preto iná sila, ktorá je proti. Ak chceme, aby blok zostal v pokoji, táto sila je statické trenie. Ale ak dovolíme, aby sa blok posúval z kopca konštantnou rýchlosťou, potom je potrebnou pevnosťou dynamické trenie.

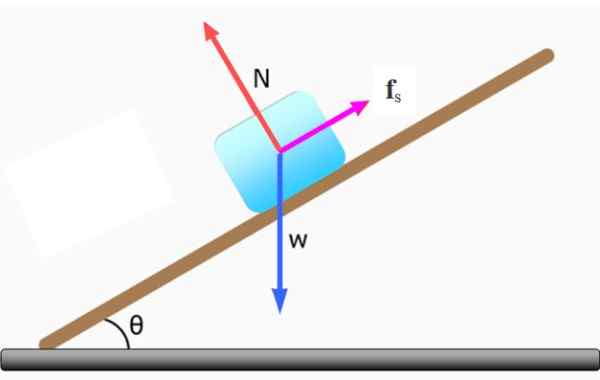Obrázok 3. Blok zostáva v statickej rovnováhe na naklonenej rovine. Zdroj: f. Zapata.

Pri absencii trenia sa blok skĺzne dole a v takom prípade nebude rovnováha.

Aby bol blok v pokoji, sily, ktoré naň pôsobia: váha W, Normálny N a statické trenie F_siež, Musia byť kompenzované. Tak:

∑ f_a = 0 → n - w_a = 0

∑ f_X = 0 → w_X - F_siež = 0

Statické trenie vyvažuje horizontálnu zložku hmotnosti: w_X = f_siež a preto:

F_siež = m . g .hriech

Cvičenie

Semafor 21.5 kg visí z homogénneho hliníkového baru AB s hmotnosťou 12 kg a 7.5 m dlhé, udržiavané horizontálnym lanom CD, ako je to znázornené na obrázku. Nájsť:

Môže vám slúžiť: Prekrytá veta: Vysvetlenie, aplikácie, vyriešené cvičenia

a) napätie kábla CD

b) Horizontálne a vertikálne komponenty sily vyvíjanej čapom na stĺpiku.

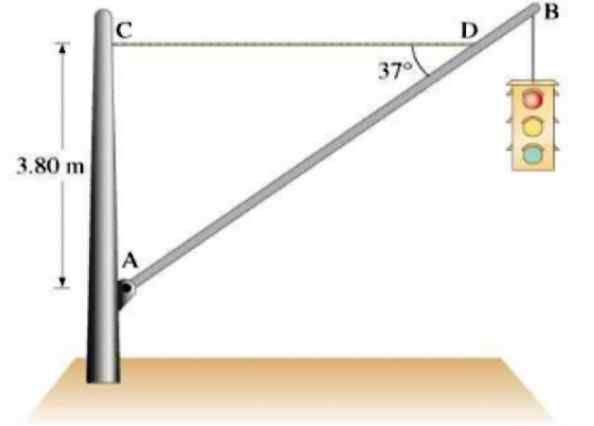Obrázok 4.- Dopravné svetlo visí z hliníkovej lišty v statickej rovnováhe. Zdroj: Giancoli. D. Fyzika s aplikáciami.

Riešenie

Schéma síl aplikovaná na tyč je postavená s hmotnosťou W, Napätie v reťazci a horizontálne a vertikálne komponenty otočnej reakcie nazývané r_X a r_a. Potom platia rovnovážne podmienky.

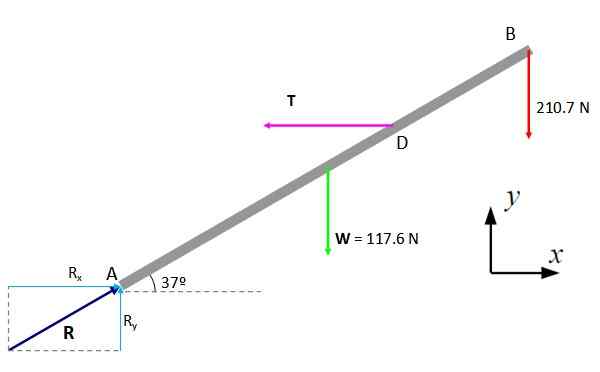Obrázok 5. Diagram voľného tela pre bar. Zdroj: f. Zapata.

Prvá podmienka

Prvý rovnovážny stav, ktorý je problémom v rovine, ponúka dve rovnice:

Σf_X = 0
Σf_a = 0

Od prvého:

R_X - T = 0

R_X = T

A druhý:

R_a - 117.6 N - 210.7 n = 0

R_a = 328.3 n

Horizontálna zložka reakcie je rovnaká ako t napätie.

Druhá podmienka

Bod A na obrázku 5 je vybraný ako zákruta, týmto spôsobom je reakčné rameno R Je neplatný, nezabudnite, že veľkosť tohto okamihu je daná:

M = f_┴ d

Kde f_┴ Je to kolmá zložka sily a D je vzdialenosť medzi osou rotácie a bodom použitia sily. Dostaneme rovnicu:

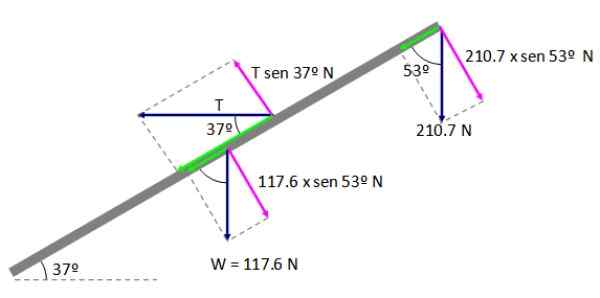Obrázok 6. Momenty týkajúce sa bodu a. Zdroj: f. Zapata.

Σm_Do = 0

(210.7 × sen 53 °) AB + (117.6 × sen 53 °) (ab/2) - (t × sen 37 °) ad = 0

Vzdialenosť je:

Ad = (3.8 m / sin 37 °) = 6.3 m

(210.7 × sen 53 ° N) (7.5 m) + (117.6 × sen 53 ° N) (3.75 m) - (t × sen 37 ° N) (6.3 m) = 0

Vykonanie uvedených operácií:

1262.04 + 352.20 - 3.8T = 0

Vymazanie t Gets:

T = 424.8 n

Z prvej podmienky, ktorú musel_X = T, preto:

R_X = 424.8 n

Záujmové témy

Podmienka prvého vyváženia.

Druhá rovnovážna podmienka.

Odkazy

1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Častice. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Wikipedia. Izostázia. Obnovené z: je.Wikipedia.orgán.