Vysvetlenie prvej rovnováhy, príklady, cvičenia

Ten Podmienka prvého vyváženia Vyžaduje si, aby bol suchý vektor všetkých síl pôsobiacich na telo neplatný, takže je v pokoji (statická rovnováha) alebo s rovnomerným priamym pohybom (dynamická rovnováha).

Táto suma síl nie je nič iné ako čistá sila, ktorá pôsobí na telo a matematicky vyjadruje tento režim:

F_Slepo = 0

∑ F = 0

postava 1. Stavitelia staroveku už použili prvý rovnovážny stav, o čom dokazuje pamätník Stonehenge. Zdroj: Pixabay.

Vo vesmíre prvá rovnovážna podmienka vedie k trom rovniciam, jedna pre každú dimenziu:

∑ f_X = 0; ∑ f_a = 0 a ∑ f_z = 0

Ak sú tieto rovnice splnené, objekt sa nepohybuje alebo ak áno, bude to s konštantnou rýchlosťou.

Pozorujeme okolo nás, uvedomujeme si, že sa neustále snažíme uspokojiť prvú rovnovážnu podmienku, aby veci nespadli.

Preto sa snaží kompenzovať gravitačnú príťažlivosť Zeme prostredníctvom podpory, laná alebo podpory niektorých, aby veci zostali na mieste a nechodili na zem.

Inokedy je potrebné zabrániť tomu, aby externé elektromagnetické polia zasahovali do prevádzky elektrických obvodov a komunikačných zariadení. V takom prípade musia byť v rovnováhe elektrické náboje.

[TOC]

Príklady

Veľké množstvo každodenných predmetov spĺňa prvú rovnovážnu podmienku, je to otázka pozornosti pozornosti:

Budovy

Stavitelia hľadajú stabilitu v konštrukciách, aby používatelia zostali v bezpečí. Cieľom statického je študovať podmienky statickej rovnováhy v budovách, mostoch, cestách a všetkých druhoch štruktúr.

Higafory a zavesené varovania

Tieto signalizačné zariadenia musia zostať pevné, aby splnili svoje funkcie, a preto podliehajú káblom, stĺpikom a prútom takým spôsobom, že je splnená podmienka prvej rovnováhy.

Môže vám slúžiť: Tretí zákon termodynamiky: vzorce, rovnice, príkladyObrázok 2. Sebafrektory a varovania visia sú predmetom tak, aby uspokojili prvú rovnovážnu podmienku. Zdroj: pxfuel.

Vodiči elektrostovej rovnováhyprívesok

Ak sa vodivé materiály, ako je meď a iné kovy, získavajú elektrický náboj, elektrostatická rovnováha sa zavedie čoskoro, čím sa zaťažuje prebytok na vodivom povrchu. Vo vnútri elektrického poľa je nula.

Tento účinok sa často používa na izoláciu elektrických a elektronických zariadení vonkajších polí pomocou tak -založenej Faradayovej klietky. Klietka je vyrobená z vodivého materiálu a obklopuje zariadenie, ktoré má byť chránené.

Počas búrok slúžia autá ako Faraday klietky tým, že chránia cestujúcich pred elektrickými šokmi.

Stropné žiarovky

V osvetľovacích systémoch, ako sú závesné žiarovky, sa používa prvá rovnováha na ich pripevnenie na strechu, na podlahu alebo stenu.

Obrázok 3. Prepracovaná strešná lampa nazývaná „pavúky“ spĺňajú prvý rovnovážny stav. Zdroj: Pixabay.

Knihy a predmety na stoloch

Objekty umiestnené na stoloch a policiach spĺňajú prvú rovnovážnu podmienku. Normálna sila, že podpora vyvíja na objekty, je zodpovedná za kompenzáciu hmotnosti.

Miera viskozity kvapaliny

Na určenie viskozity kvapaliny sférický predmet, známeho priemeru, ktorý bude vidieť jeho rýchlosť kvôli odporu, ktorý bude klesať vo vnútri. Rýchlosť gule je konštantná a je v dynamickej rovnováhe.

Väčšia viskozita kvapaliny, menej rýchlosti, s akou sa guľa pohybuje vo vnútri.

Kroky na použitie prvej rovnovážnej podmienky

-Vytvorte voľný diagram tela, ktorý ukazuje všetky sily, ktoré pôsobia na tele (vynechajte, čo telo vyvíja na ostatných).

Môže vám slúžiť: fyzika v stredoveku

-Vyberte karteziánsky súradnicový systém, zabezpečte, že ak je to možné, sú sily umiestnené na ktorejkoľvek zo sekerov. Pozitívna adresa sa zvyčajne prijíma v zmysle pohybu alebo v možnom pohybe.

-Určte karteziánske komponenty každej sily.

-Aplikujte Newtonov druhý zákon pre každú zložku, ako je stanovené na začiatku, existuje systém rovníc.

-Vyriešte systém rovníc získaných v predchádzajúcom kroku.

Vyriešené cvičenia

- Cvičenie vyriešené 1

Blok postavy, hmotnosti m, Pohybuje sa z kopca v rovine uhla 9 s konštantnou rýchlosťou. Vypočítajte hodnotu koeficientu kinetického trenia μ_{klimatizovať}, Ak je hmotnosť bloku m = 5 kg a 9 = 37 °.

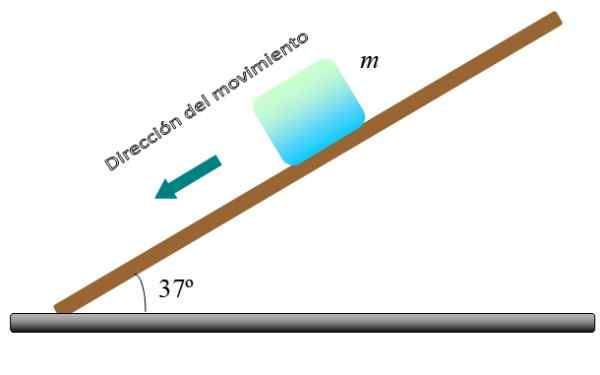Obrázok 4. Blok sa posúva konštantnou rýchlosťou v naklonenej rovine. Zdroj: f. Zapata.

Riešenie

Prvým krokom je nakresliť diagram voľného tela a zvoliť karteziánsky súradnicový systém, ktorý vyjadruje každý vektor sily. Sily pôsobiace na bloku sú:

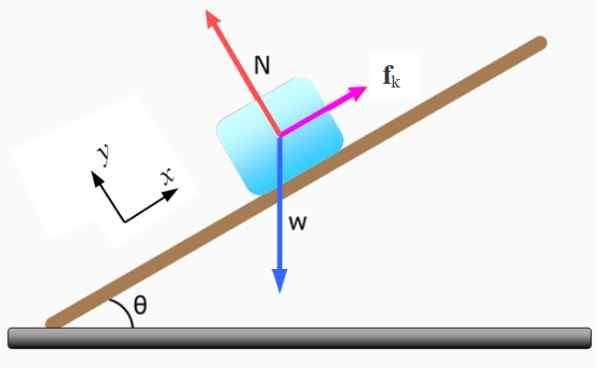Obrázok 5. Diagram voľného tela pre blok. Zdroj: f. Zapata.

-Normálny N Cvičené sklonenou rovinou je kolmá na povrch tohto povrchu.

-Váha W Je nasmerovaný vertikálne nadol.

-Kinetické trenie F_{klimatizovať} To je proti pohybu. Keby neexistoval, telo by sa pohybovalo z kopca s zrýchlením rovnajúcim sa g.Senátor.

Ako váha W Je naklonený vzhľadom na vybrané súradnicové osi, musí sa rozdeliť do svojich karteziánskych komponentov:

W_X = mg.Sen 37 ° = 5 kg x 9,8 m/s² x Sin 37 ° = 29. 5 n
W_a = mg.cos 37 ° = 5 kg x 9,8 m/s² x cos 37 ° = 39.1 n

Newtonov druhý zákon sa teraz uplatňuje, čo zodpovedá každej sume 0, pretože blok nemá zrýchlenie pri pohybe s konštantnou rýchlosťou:

∑ f_a = N - w_a = 0
∑ f_X = W_X - F_{klimatizovať} = 0

Veľkosť kinetického trenia je úmerná veľkosti normálu, čo je koeficient kinetického trenia μ_{klimatizovať} Konštantná proporcionalita.

Môže vám slúžiť: Absolútny tlak: vzorec, ako sa vypočíta, príklady, cvičenia

F_{klimatizovať} = μ_{klimatizovať} N

V rovnakom čase:

N = w_a = 39.1 n

A tiež:

F_{klimatizovať} = W_X

Preto:

29. 5 n = μ_{klimatizovať} X 39.1 n

μ_{klimatizovať} = 29. 5/39.1 = 0.75

- Cvičenie vyriešené 2

Vypočítajte veľkosť napätia, ktoré podporujú masové dopravné svetlo 33 kg, znázornené na obrázku:

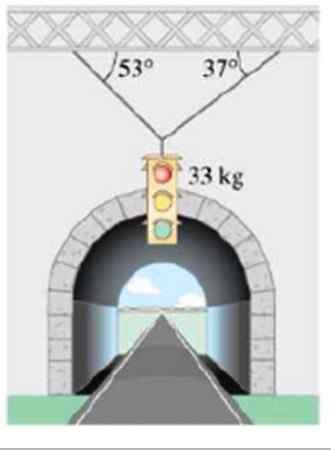Obrázok 6. Semafor visí pomocou káblov. Zdroj: Giancoli. Fyzika s aplikáciami.

Riešenie

Schéma voľného tela sa vykonáva tak pre semafor, ako aj pre uzol, ktorý drží káble:

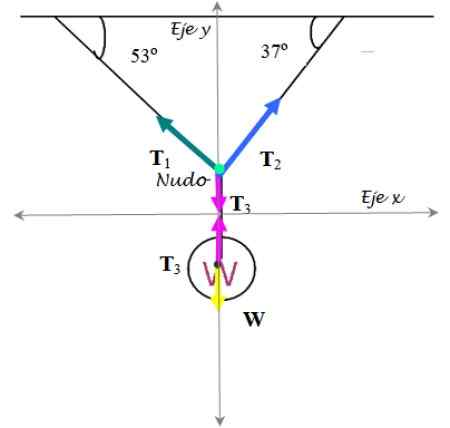Obrázok 7. Diagram voľného tela pre cvičenie vyriešené 2. Zdroj: f. Zapata.

Semafor

O tom zákon: napätie t₃ hore a váha W. Preto:

∑ f_a = W - t₃ = 0

Preto:

Tón₃ = 33 kg x 9.8 m/s² = 323.4 n

Uzol

Napätie sa rozpadá vo svojich karteziánskych komponentoch:

∑ f_a = T₁ Sen 53 ° + t₂ Sen 37 ° - T₃ = 0
∑ f_X = T₂ Cos 37 ° - t₁ Cos 53 ° = 0

A získajú sa nasledujúci systém lineárnych rovníc s dvoma neznámymi₁  a t₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

Riešenie tohto systému rovníc je: T₁ = 258.7 n a t₂ = 194.0 n

Záujmové témy

Rovnováha.

Druhá rovnovážna podmienka.

Odkazy

1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Častice. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Wikipedia. Statické (mechanické). Obnovené z: je.Wikipedia.orgán.