Empirické pravidlo, ako ho uplatňovať, na čo ide, cvičenia vyriešené

A Empirické pravidlo Je to výsledok praktických skúseností a pozorovania skutočného života. Napríklad môžete vedieť, že druhy vtákov je možné pozorovať na niektorých miestach v každom roku a že pozorovanie je možné stanoviť „pravidlo“, ktoré opisuje životné cykly týchto vtákov.

V štatistike sa empirické pravidlo vzťahuje na formu zoskupenia pozorovaní okolo centrálnej hodnoty, priemeru alebo priemeru v štandardných odchýlkoch.

Predpokladajme, že máte skupinu ľudí s priemernou výškou 1.62 metrov a štandardná odchýlka 0.25 metrov, potom by empirické pravidlo umožnilo definovať napríklad, koľko ľudí by bolo v intervale priemeru viac alebo menej štandardnou odchýlkou?

Podľa pravidla je 68% údajov viac -menej štandardnou odchýlkou ​​priemeru, to znamená, že 68% skupiny ľudí bude mať výšku medzi 1.37 (1.62-0.25) a 1.87 (1.62+0.25) merače.

[TOC]

Odkiaľ pochádza empirické pravidlo?

Empirické pravidlo je zovšeobecnenie Tchebbyshevovej vety a normálne rozdelenie.

Tchebbyshevova veta

Tchebbyshevova veta hovorí, že: Pre určitú hodnotu k> 1 je pravdepodobnosť, že náhodná premenná patrí medzi priemerne menej k násobku štandardnej odchýlky a priemer viac k krát viac k nárazu, štandardná odchýlka je väčšia alebo rovná (1-1 /k²).

Výhodou tejto vety je, že sa vzťahuje na diskrétne alebo kontinuálne náhodné premenné s akýmkoľvek rozdelením pravdepodobnosti, ale pravidlo z nej nie je vždy veľmi presné, pretože závisí od symetrie distribúcie. Čím viac asymetrickejšie je distribúcia náhodnej premennej, menej upravená na pravidlo, bude jej správanie.

Empirické pravidlo definované z tejto vety je:

Ak k = √2, hovorí sa, že 50% údajov je v intervale: [µ - √2 s, µ + √2 s]

Ak k = 2, hovorí sa, že 75% údajov je v intervale: [µ - 2 s, µ + 2 s]

Ak k = 3, hovorí sa, že 89% údajov je v intervale: [µ - 3 s, µ + 3 s]

Normálna distribúcia

Normálne rozdelenie alebo Gauss Bell umožňuje stanoviť empirické pravidlo alebo pravidlo 68 - 95 - 99.7.

Môže vám slúžiť: Pomer

Pravidlo je založené na pravdepodobnosti výskytu náhodnej premennej v intervaloch medzi priemernou nižšou, dvoma alebo tromi štandardnými odchýlkami a priemerom plus jedna, dve alebo tri štandardné odchýlky.

Empirické pravidlo definuje nasledujúce intervaly:

68.27% údajov je v intervale: [µ - S, µ + S]

95.45% údajov je v intervale: [µ - 2s, µ + 2s]

99.73% údajov je v intervale: [µ - 3s, µ + 3s]

Na obrázku vidíte, ako sú tieto intervaly prezentované a vzťah medzi nimi zvýšením šírky grafickej základne.

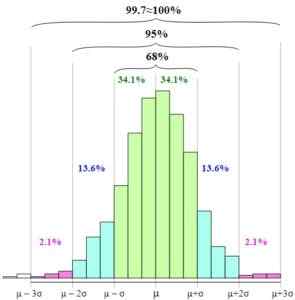Empirické pravidlo. Melikamp [CC BY-SA 4.0 (https: // creativeCommons.org/)] štandardizácia náhodnej premennej, tj expresia náhodnej premennej z hľadiska štandardnej alebo normálnej premennej, zjednodušuje použitie empirického pravidla, pretože premenná z má priemernú rovnú nule a štandardná odchýlka rovná do jedného.

Preto uplatňovanie empirického pravidla na stupnici štandardnej normálnej premennej z, definuje nasledujúce intervaly:

68.27% údajov je v intervale: [-1, 1]

95.45% údajov je v intervale: [-2, 2]

99.73% údajov je v intervale: [-3, 3]

Ako uplatniť empirické pravidlo?

Empirické pravidlo vám umožňuje skrátiť výpočty pri práci s normálnym rozdelením.

Predpokladajme, že skupina 100 študentov vysokých škôl má priemerný vek 23 rokov, so štandardnou odchýlkou ​​2 roky. Aké informácie umožňuje empirické pravidlo?

Uplatňovanie empirického pravidla znamená nasledujúce kroky:

1- Zostavte intervaly pravidiel

Pretože priemer je 23 a štandardná odchýlka je 2, potom intervaly sú:

[µ - S, µ + S] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Vypočítajte počet študentov v každom intervale podľa percent

(100)*68.27% = 68 študentov približne

(100)*95.45% = približne 95 študentov

(100)*99.73% = 100 študentov

3- Intervaly veku sú spojené s množstvom študentov a interpretované

Najmenej 68 študentov má 21 až 25 rokov.

Môže vám slúžiť: Opisná štatistika: História, charakteristiky, príklady, koncepty

Najmenej 95 študentov je vo veku 19 až 27 rokov.

Prakticky 100 študentov má 17 až 29 rokov.

Čo je empirické pravidlo pre?

Empirické pravidlo je rýchly a praktický spôsob analýzy štatistických údajov, čo je čoraz spoľahlivejšie v rozsahu, v akom je distribúcia blízko symetrie.

Jeho užitočnosť závisí od poľa, v ktorej sa používa, a na otázky, ktoré vznikajú. Je veľmi užitočné vedieť, že výskyt hodnôt troch štandardných odchýlok je takmer nepravdepodobný pod alebo nad priemerom, a to aj pre normálne distribučné premenné, najmenej 88.8% prípadov je v intervale troch sigma.

V sociálnych vedách je všeobecne presvedčivým výsledkom interval priemeru viac -menej dvaja sigma (95%), zatiaľ čo vo fyzike častíc vyžaduje nový účinok interval päť Sigmas (99.99994%), ktorý sa má považovať za objav.

Vyriešené cvičenia

Králiky v rezerve

V rezervácii voľne žijúcich živočíchov sa odhaduje, že v priemere 16.000 králikov so štandardnou odchýlkou ​​500 králikov. Ak nie je možné distribúciu premennej „počet králikov v rezerve“, je to možné.000 a 17.000 králikov?

Interval je možné prezentovať v týchto podmienkach:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Preto: [15000, 17000] = [µ - 2 s, µ + 2 s]

Pri použití Tchebbyshevovej vety existuje pravdepodobnosť najmenej 0.75, že populácia králikov rezervy voľne žijúcich živočíchov je medzi 15.000 a 17.000 králikov.

Priemery detí z krajiny

Priemerná hmotnosť jedného ročníka detí je zvyčajne distribuovaná s priemerom 10 kilogramov a štandardnou odchýlkou ​​približne 1 kilogram.

a) Odhadnite percento jedného ročníka detí v krajine, ktoré majú priemernú váhu medzi 8 a 12 kilogramami.

8 = 10 - 2 = 10 - 2 (1) = u - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Preto: [8, 12] = [µ - 2s, µ + 2s]

Môže vám slúžiť: Tukey Test: Čo je v prípade príkladu vyriešené cvičenie

Podľa empirického pravidla možno potvrdiť, že 68.27% detí v krajine má hmotnosť 8 až 12 kilogramov.

b) Aká je pravdepodobnosť nájdenia jedného roka s dĺžkou 7 kilogramov alebo menšej hmotnosti?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Je známe, že 7 kilogramov hmotnosti predstavuje hodnotu µ - 3s, ako aj je známe, že 99.73% detí je medzi 7 a 13 kilogramami hmotnosti. To odchádza iba 0.27% z celkových detí pre extrémne. Polovica z nich, 0.135%, má 7 kilogramov hmotnosti alebo menej a druhú polovicu, 0.135%, má 11 kilogramov hmotnosti alebo viac.

Dá sa teda dospieť k záveru, že existuje pravdepodobnosť 0.00135, že dieťa má 7 kilogramov hmotnosti alebo menej.

c) Ak obyvateľstvo krajiny dosiahne 50 miliónov obyvateľov a deti 1 roka?

9 = 10 - 1 = µ - s

11 = 10 + 1 = µ + s

Preto: [9, 11] = [u - s, µ + s]

Podľa empirického pravidla 68.27% z jedného ročníka detí je v intervale [u -s, µ + s]

V krajine je 500 000 detí s jedným rokom (1% z 50 miliónov), takže 341350 detí (68.27% z 500 000) má hmotnosť 9 a 11 kilogramov.

Odkazy

1. Abraira, V. (2002). Štandardná odchýlka a štandardná chyba. Časopis. Na webe obnovený.Archív.orgán.
2. Freund, r.; Wilson, w.; Mohr, D. (2010). Štatistické metódy. Tretie vydanie. Academic Press-Elsevier Inc.
3. Alicante Server (2017). Empirické pravidlo (štatistické pojmy). Slovník sa zotavil.natiahnutý serverom.com.
4. Lind, D.; Marchal, w.; Wathen, s. (2012). Štatistiky uplatňované pre podnikanie a hospodárstvo. Desiaty ed. McGraw-Hill/Inter-American z Mexika S. Do.
5. Salinas, h. (2010). Štatistika. Zotavené z UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Úvod do biostatistiky. Druhé vydanie. Dover Publications, Inc.
7. Spiegel, m. (1976). Pravdepodobnosť a štatistika. Séria Schaum. McGraw-Hill/Inter-American z Mexika S. Do.
8. Spiegel, m.; Stephens, L. (2008). Štatistika. Štvrté vydanie. McGraw-Hill/Inter-American z Mexika S. Do.
9. Recenzia Stat119 (2019). Empirické otázky týkajúce sa pravidiel riešenia. Zdroj: zo stat19Review.com.
10. (2019). 68-95-99.7 Pravidlo. Získaný z.Wikipedia.orgán.