Homocedicita, čo je, dôležitosť a príklady

Ten Homocedicita V prediktívnom štatistickom modeli sa vyskytuje, ak vo všetkých dátových skupinách jedného alebo viacerých pozorovaní zostáva rozptyl modelu vzhľadom na vysvetľujúce (alebo nezávislé) premenné konštantné.

Regresný model môže byť homocedastický alebo nie, v takom prípade hovoríme o tom heterocedicita.

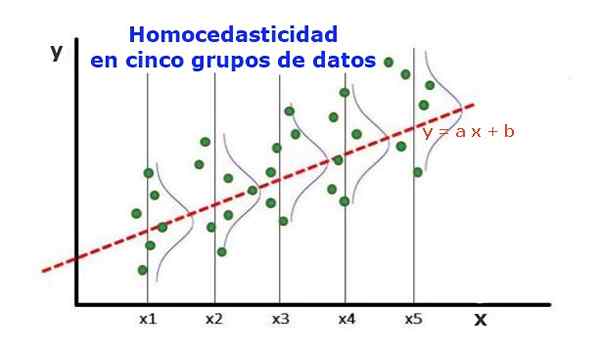
postava 1. Päť skupín údajov a regresné úpravy množiny. Rozdiel týkajúci sa predpovedanej hodnoty je v každej skupine rovnaký. (Upav-Library.org)

Štatistický regresný model niekoľkých nezávislých premenných sa nazýva homocedastický, iba ak rozptyl predpokladanej variabilnej chyby (alebo štandardná odchýlka závislej premennej) zostáva rovnomerná pre rôzne skupiny vysvetľujúcich alebo nezávislých premenných.

V piatich skupinách údajov na obrázku 1 sa rozptyl vypočítal v každej skupine, vzhľadom na hodnotu odhadnutú regresiou, ktorá sa v každej skupine stala rovnakou. Tiež sa predpokladá, že údaje sledujú normálne rozdelenie.

Na grafickej úrovni to znamená, že body sú rovnako rozptýlené alebo rozptýlené okolo predpokladanej hodnoty úpravou regresie a že regresný model má rovnakú chybu a platnosť pre rozsah vysvetľujúcej premennej.

[TOC]

Dôležitosť homocedicity

Na ilustráciu významu homocedasticity v prediktívnej štatistike je potrebné kontrastovať s opačným javom, heterocedicity.

Homocedasticita verzus heteroceedicita

V prípade obrázku 1, v ktorom je homocedicita, je splnená to:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Kde var ((yi-ii); xi) predstavuje rozptyl, pár (xi, yi) predstavuje skutočnosť skupiny I, zatiaľ čo yi je hodnota, ktorá predpovedá regresiu pre priemernú hodnotu Xi skupiny. Rozptyl údajov skupiny I sa vypočíta takto:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Naopak, keď dôjde k heteroceedicite, regresný model nemusí byť platný pre celú oblasť, v ktorej bol vypočítaný. Obrázok 2 ukazuje príklad tejto situácie.

Môže vám slúžiť: Čo sú interné striedavé uhly? (S cvičeniami)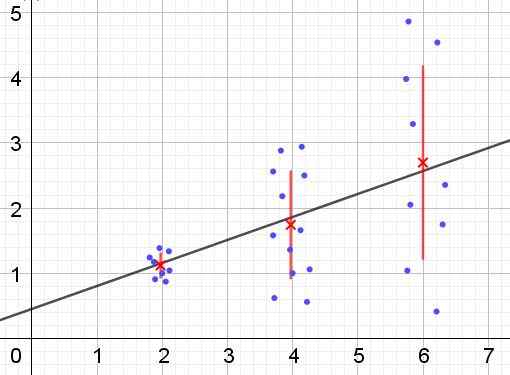 Obrázok 2. Dátová skupina, ktorá má heteroceedicitu. (Vlastné rozpracovanie)

Na obrázku 2 sú tri skupiny údajov a súbor množiny reprezentovaný lineárnou regresiou. Je potrebné poznamenať, že údaje v druhej a v tretej skupine sú rozptýlené ako v prvej skupine. Graf na obrázku 2 tiež ukazuje priemernú hodnotu každej skupiny a jej chybový riadok ± σ, čo je štandardná odchýlka σ každej dátovej skupiny. Malo by sa pamätať na to, že štandardná odchýlka σ je odmocninou rozptylu.

Je zrejmé, že v prípade heterocedicity sa chyba odhadu regresie mení v rozsahu hodnôt vysvetľujúcej alebo nezávislej premennej av intervaloch, kde je táto chyba veľmi veľká nepoužiteľné.

V regresnom modeli musia byť chyby alebo odpad (y -y) distribuované s rovnakou rozptylom (σ^2) v celom intervale nezávislých premenných hodnôt. Z tohto dôvodu musí dobrý regresný model (lineárny alebo nelineárny) prejsť testom homocedasticity. 

Testy homoceedicity

Body znázornené na obrázku 3 zodpovedajú údajom štúdie, ktorá hľadá vzťah medzi cenami (v dolároch) domov v závislosti od veľkosti alebo oblasti v meracích štvorcoch.

Prvým modelom, ktorý je nacvičený, je lineárna regresia. V prvom rade sa poznamenáva, že koeficient určovania R^2 je dosť vysoký (91%), takže je možné predpokladať, že prispôsobenie je uspokojivé.

Od grafu nastavenia sa však dajú jasne odlíšiť dve oblasti. Jeden z nich, ten vpravo zamknutý v ovále, sa stretáva s homocedasticitou, zatiaľ čo oblasť ľavice nemá homocedasticitu.

Môže vám slúžiť: známka polynómu: Ako je určené, príklady a cvičenia

To znamená, že predikcia regresného modelu je primeraná a spoľahlivá v rozsahu medzi 1800 m^2 až 4800 m^2, ale veľmi neprimeraná mimo tejto oblasti. V heterocedickej oblasti je nielen chyba veľmi veľká, ale zdá sa, že aj údaje sledujú ďalší trend odlišný od navrhnutého v lineárnom regresnom modeli.

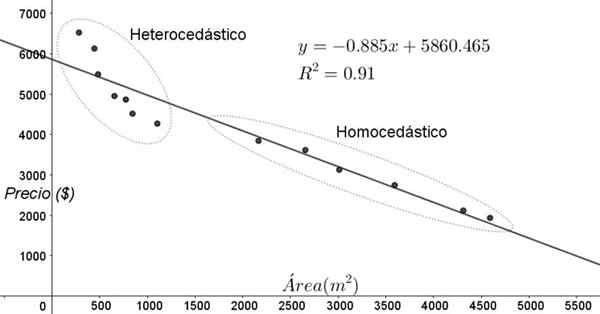Obrázok 3. Ceny bývania verzus oblasť a prediktívny model lineárnou regresiou, ktorá ukazuje homocedasticitu a heterocedicitné oblasti. (Vlastné rozpracovanie)

Graf disperzie údajov je najjednoduchší a najobľúbenejší test ich homocedasticity, niekedy to však nie je také zrejmé ako v príklade na obrázku 3, je potrebné uchýliť sa k grafike s pomocnými premennými.

Štandardizované premenné

S účelom oddelenia oblastí, v ktorých je splnená homocedasticita, a v ktorých nie sú zavedené štandardizované premenné ZRE a Zreded:

Zres = abs (y - y)/σ

Zpred = y/σ

Je potrebné poznamenať, že tieto premenné závisia od použitého regresného modelu, pretože ide o hodnotu regresnej predikcie. Nižšie je uvedený disperzný graf ZRES vs Zred pre ten istý príklad:

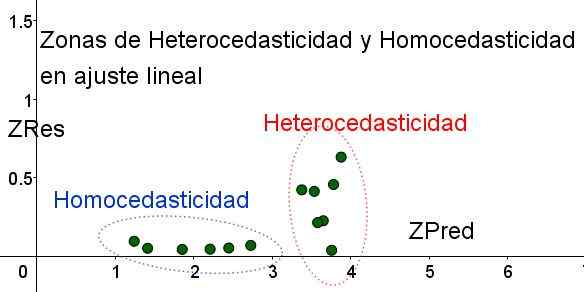Obrázok 4. Je potrebné poznamenať, že v zóne homocedasticity ZRE zostáva v predikčnej oblasti jednotný a malý (vlastné vypracovanie).

V grafe na obrázku 4 so štandardizovanými premennými je oblasť, v ktorej je zvyšková chyba malá a rovnomerná, jasne oddelená, vzhľadom na oblasť, ktorá nie. V prvej oblasti je splnená homocedasticita, zatiaľ čo zvyšková chyba je veľmi variabilná a veľká.

Úprava regresie sa používa na rovnakú dátovú skupinu 3. Výsledok je znázornený na nasledujúcom obrázku:

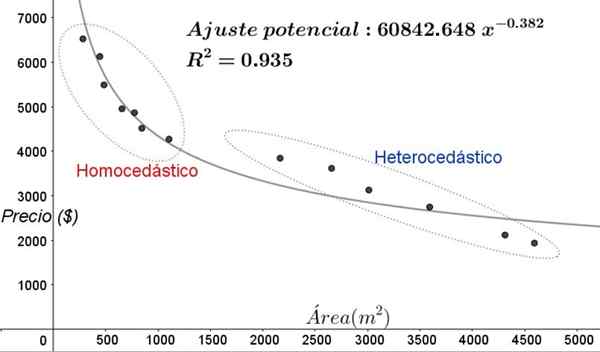Obrázok 5. Nová homocedasticita a heterocedicita v úprave údajov s nelinimálnym regresným modelom. (Vlastné rozpracovanie).

V grafe na obrázku 5 by sa mali jasne všimnúť homocedické a heterocedikastické oblasti. Malo by sa tiež poznamenať, že tieto oblasti sa vymieňali s ohľadom na tie, ktoré boli vytvorené v modeli lineárneho úpravy.

Môže vám slúžiť: typy uhlov, charakteristík a príklady

V grafe na obrázku 5 je zrejmé, že aj keď je koeficient určenia úpravy pomerne vysoký (93,5%), model nie je vhodný pre celý interval vysvetľujúcej premennej, pretože údaje pre hodnoty staršie ako 2000 nie je vhodný m^2 majú heterocedasticitu.

Neografické testy homocedasticity

Jedným z najpoužívanejších neografických testov na overenie, či je splnená homocedasticita, je Test Breusch-Pagan.

Všetky podrobnosti o tomto teste nebudú uvedené v tomto článku, ale jeho základné charakteristiky a jeho kroky sú všeobecne načrtnuté:

1. Regresný model sa aplikuje na NA NA NA NA NA NÁKLADY A IT sa vypočítava s ohľadom na hodnotu odhadnutú podľa modelu σ^2 = ∑j (yj - y)^2/n.
2. Je definovaná nová premenná ε = ((yj - y)^2) / (σ^2)
3. Rovnaký regresný model sa používa na novú premennú a vypočíta sa jej nové regresné parametre.
4. Určuje sa kritická hodnota Chi Square (χ^2), čo je polovica súčtu štvorcov nový odpad v premennej ε.
5. Tabuľka distribučnej distribúcie Chi sa používa vzhľadom na úroveň významnosti na osi X (zvyčajne 5%) a počet stupňov voľnosti (#FOF regresné premenné okrem jednotky), aby sa získala hodnota dosky.
6. Kritická hodnota získaná v kroku 3 sa porovnáva s hodnotou uvedenou v tabuľke (χ^2).
7. Ak je kritická hodnota pod hodnotou tabuľky, máte nulovú hypotézu: existuje homocedicita
8. Ak je kritická hodnota nad hodnotou tabuľky, máte alternatívnu hypotézu: neexistuje homocedasticita.

Väčšina štatistických počítačových balíkov ako: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic a niekoľko ďalších zahŕňa test homocedasticity Breusch-pagan. Ďalší test na overenie uniformity rozptylu Skúška.

Odkazy

1. Box, Hunter a Hunter. (1988) Štatistiky pre výskumných pracovníkov. Zvrátil som redaktorov.
2. Johnston, J (1989). Metódy ekonometrie, editory Viccens --ils.
3. Murillo a González (2000). Príručka pre ekonomiku. University of Las Palmas de Gran Canaria. Zdroj: ULPGC.je.
4. Wikipedia. Homocedicita. Obnovené z: je.Wikipedia.com
5. Wikipedia. Homoscedasticita. Zdroj: In.Wikipedia.com