Koncept náhodného experimentu, vzorový priestor, príklady

Hovorí sa o tom náhodný experiment Ak je výsledok každej konkrétnej skúšky nepredvídateľný, aj keď je možné stanoviť pravdepodobnosť výskytu určitého výsledku.

Malo by sa však objasniť, že nie je možné reprodukovať rovnaký výsledok náhodného systému s rovnakými počiatočnými parametrami a podmienkami v každej štúdii experimentu.

postava 1. Spustenie kocky je náhodný experiment. Zdroj: Pixabay.

Dobrým príkladom náhodného experimentu je spustenie kocky. Aj keď sa postaráte o spustenie kocky rovnakým spôsobom, pri každom pokuse sa získa nepredvídateľný výsledok. Jediné, čo možno potvrdiť, je, že výsledkom môže byť niektoré z nasledujúcich: 1, 2, 3, 4, 5 alebo 6.

Spustenie meny je ďalším príkladom náhodného experimentu s iba dvoma možnými výsledkami: tvár alebo tesnenie. Aj keď je mena spustená z rovnakej výšky a rovnakým spôsobom, bude vždy prítomný náhodný faktor, čo vedie k neistote pri každom novom pokuse.

Opak náhodného experimentu je deterministický experiment. Napríklad je známe, že zakaždým, keď sa voda varí na hladine mora, teplota varu je 100 ° C. Ale nikdy sa to nestane, že udržiavanie rovnakých podmienok je výsledkom niekedy 90 ° C, ďalších 12 0 ° C a niekedy 100 ° C.

[TOC]

Vzorový priestor

Sada všetkých možných výsledkov náhodného experimentu sa nazýva vzorový priestor. V náhodnom experimente spustenia kocky je priestor vzorky:

D = 1, 2, 3, 4, 5, 6.

Pokiaľ ide o uvedenie meny, vzorový priestor je:

M = face, pečať.

Udalosť alebo udalosť

V náhodnom experimente a udalosť Je to výskyt alebo nie určitý výsledok. Napríklad v prípade spustenia meny je udalosť alebo udalosť drahá.

Môže vám slúžiť: homológne strany

Ďalšia udalosť v náhodnom experimente by mohla byť takto: že pri spustení kocky sa vydá číslo menej ako tri.

V prípade, že sa udalosť uskutoční, potom je sada možných výsledkov sada:

E = 1, 2, 3

Na druhej strane je to podskupina priestoru alebo množiny vzoriek:

M = 1, 2, 3, 4, 5, 6.

Príklady

Nižšie sú uvedené niekoľko príkladov, ktoré ilustrujú vyššie uvedené:

Príklad 1

Predpokladajme, že sa hodia dve mince, jedna po druhej. Požaduje sa:

a) Uveďte, či ide o náhodný experiment alebo naopak, deterministický experiment.

b) Aký je vzorový priestor tohto experimentu?

c) Uveďte celú udalosť A, ktorá zodpovedá experimentu, má výsledok tváre a známky.

d) Vypočítajte pravdepodobnosť, že udalosť nastane.

e) Nakoniec nájdite pravdepodobnosť, že udalosť B: Nezjavte sa tvárou v tvár výsledku.

Riešenie 

a) Je to náhodný experiment, pretože neexistuje spôsob, ako predpovedať, čo bude výsledkom spustenia týchto dvoch mincí.

b) Vzorový priestor je sada všetkých možných výsledkov:

S = (c, c), (c, s), (s, c), (s, s)

c) Udalosť a, v prípade uvedeného prípadu, môže mať tieto výsledky:

A = (c, s), (s, c)

d) Pravdepodobnosť udalosti A sa získa z vydelenia počtu prvkov množiny a medzi počet prvkov sady zodpovedajúcej vzorovému priestoru:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Sada možných výsledkov zodpovedajúcich udalosti B (neobjavujúca sa tvárou viedlo k výsledku) je:

Môže vám slúžiť: Perfect Square Trinomial

B = (s, s)

Pravdepodobnosť, že udalosť B sa vyskytne v eseji, je pomer medzi počtom možných výsledkov B medzi počtom celkových prípadov:

P (b) = ¼ = 0.25 = 25%.

Príklad 2

Taška obsahuje 10 bielych guličiek a 10 čiernych guličiek. Z tašky sú náhodne odstránené a bez toho, aby sa pozerali do troch guľôčok postupne. 

a) Stanovte priestor vzorky tohto náhodného experimentu.

b) Stanovte súbor výsledkov zodpovedajúcich udalosti, ktorá je taká, že po experimente sú dve čierne mranice.

c) Udalosť B má získať najmenej dve čierne mranice, určiť set b výsledkov pre túto udalosť.

d) Aká je pravdepodobnosť, že sa udalosť uskutoční?

e) Nájdite pravdepodobnosť, že udalosť b.

f) Určite pravdepodobnosť, že výsledkom náhodného experimentu je, že aspoň jeden čierny mramor. Táto udalosť sa bude nazývať c.

Obrázok 2. Čierne a čierne guličky pre náhodné experimenty. Zdroj: Needpix.

Roztok

Na zostavenie priestoru vzorky je užitočné vytvoriť stromový diagram, ako napríklad ten, ktorý je znázornený na obrázku 3:

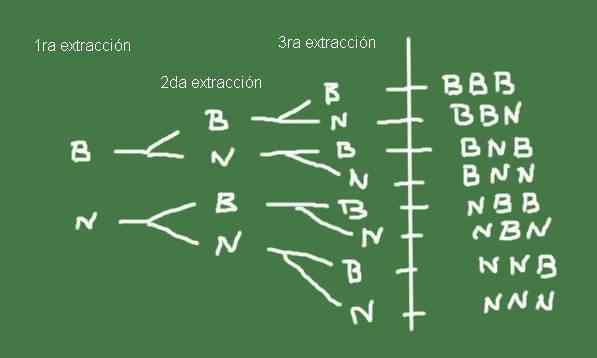Obrázok 3. Schéma stromov Pre príkladom 2. Pripravil Fanny Zapata.

Sada možných výsledkov extrahovania troch guličiek z vrecka s rovnakým počtom čiernych a čiernych guličiek je presne vzorkovacím priestorom tohto náhodného experimentu.

Ω = (B, B, B), (B, B, N), (B, N, B), (B, N, N), (N, B, B), (N, B, N) (n, n, b), (n, n, n)

Riešenie B

Súbor možných výsledkov zodpovedajúcich udalosti A, ktorá spočíva v tom, že má dva čierne guličky, je:

Môže vám slúžiť: Súčet Riemann: História, vzorce a vlastnosti, cvičenia

A = (b, n, n), (n, b, n), (n, b)

Riešenie c

Udalosť B je definovaná ako: „mať najmenej dve čierne guličky po náhodnej extrakcii troch z nich“. Sada možných výsledkov pre udalosť B je:

B = (b, n, n), (n, b, n), (n, b), (n, n, n)

Riešenie d

Pravdepodobnosť udalosti A je pomer medzi počtom možných výsledkov pre túto udalosť a celkovým počtom možných výsledkov, to znamená počet prvkov vzorového priestoru.

P (a) = n (a) / n (Ω) = 3/8 = 0.375 = 37.5%

Takže ich je 37.5% Pravdepodobnosť, že po náhodne extrahuje tri guľky z vrecka, 5%. Ale nezabudnite, že v žiadnom prípade nemôžeme predpovedať presný výsledok experimentu.

Riešenie e

Pravdepodobnosť, že udalosť B je uvedená, pozostávajúca z najmenej jedného čierneho mramoru je:

P (b) = n (b) / n (Ω) = 4/8 = 0.5 = 50%

To znamená, že možnosť udalosti B sa rovná pravdepodobnosti, ktorá sa nevyskytuje. 

Riešenie f

Pravdepodobnosť získania najmenej jedného čierneho mramoru po troch z nich sa rovná 1 menej pravdepodobnosťou, že výsledkom sú „tri biele mraby“.

P (c) = 1 - p (b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Teraz môžeme overiť tento výsledok a poznamenať, že počet možností vzhľadom na udalosť C sa rovná počtu prvkov možných výsledkov pre udalosť C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) (n, n, n)

N (c) = 7

P (c) = n (c) / n (Ω) = ⅞ = 87.5%

Odkazy

1. Kanál. Náhodný experiment. Obnovené z: YouTube.com.
2. Matematický. Náhodný experiment. Obnovené z: YouTube.com
3. Pishro Nick H . Úvod do pravdepodobnosti. Zdroj: Pravdepodobnosť.com
4. Štrbina. Pravdepodobnosť a štatistika pre inžinierov. Mc-Graw Hill.
5. Wikipedia. Experiment (teória pravdepodobnosti). Zdroj: In.Wikipedia.com
6. Wikipedia. Deterministická udalosť. Obnovené z: je. Wikipedia.com
7. Wikipedia. Náhodný experiment. Obnovené z: je.Wikipedia.com