Vzorec Simpsona pravidla, demonštrácia, príklady, cvičenia

Ten Pravidlo Simpson Je to metóda na výpočet približne definovaných integrálov. Je založená na rozdelení intervalu integrácie na dvojicu sub-intervalo rovnako rozmiestnených.

Extrémne hodnoty dvoch po sebe idúcich čiastkových intervalov definujú tri body, ktoré upravujú parabolu, ktorej rovnica je polynóm druhého stupňa. 

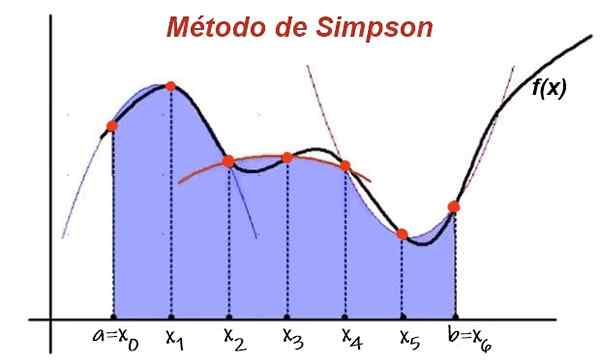
postava 1. V metóde Simpsona je integrovaný interval rozdelený do páru intervalov rovnakej šírky. Funkcia je aproximovaná podobenstvom v každých 2 čiastkových intervaloch a integrálnymi prístupmi súčtu oblasti pod podobenstvom. Zdroj: UPV.je.

Potom je oblasť pod krivkou funkcie v dvoch po sebe idúcich intervaloch aproximovaná interpolačnou polynomiálnou oblasťou. Pridanie príspevku do oblasti pod podobenstvom všetkých nasledujúcich podintervalov existuje približná hodnota integrálu.

Na druhej strane, pretože integrál podobenstva je možné presne vypočítať algebraicky, potom je možné nájsť analytický vzorec pre približnú hodnotu definovaného integrálu. Je známy ako Simpson.

Chyba takto získaného približného výsledku klesá v rozsahu, v akom je počet podskupín n väčší (je m krútiaci moment).

Pod výrazom bude uvedený, ktorý umožňuje odhad hornej úrovne chyby priblíženia k integrálu I, keď sa uskutočnilo oddiely pravidelných subintervalov celkového intervalu [a, b] [b].

[TOC]

Vzorec

Integračný interval [a, b] je rozdelený na N subintervaly, pričom n je krútiaci moment. Šírka každého pododdielu bude:

H = (b - a)/n

Týmto spôsobom je v intervale [a, b] vyrábaný oddiel:

X0, x1, x2, ..., xn-1, xn

Byť x0 = a, x1 = x0 + h, x2 = x0 + 2h,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Môže vám slúžiť: rozdiel medzi kruhom a obvodom (s príkladmi)

Vzorec, ktorý umožňuje približne vypočítať definovanú integrálnu a kontinuálnu funkciu a najlepšie mäkký v intervale [a, b] je:

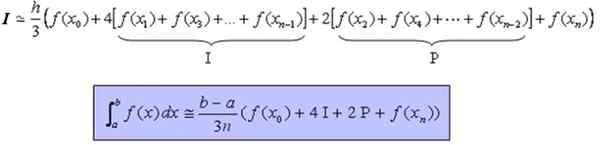
Demonštrácia

Na získanie vzorca Simpsona v každom subintervale [xi, xi+2] sa funkcia f (x) blíži o polynóm p (x) (podobenstvo), ktorý prechádza tromi bodmi: [xi, f (f (f (f (f (f (f (f ( (F (F (F (F (F (F (F (F (F (F (F Xi)]; [Xi+1, f (xi+1)] a [xi+2, f (xi+2)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]].

Potom sa integrálny polynóm P (x) vypočíta v [xi, xi+2], ktorý v tomto intervale približuje integrál funkcie f (x).

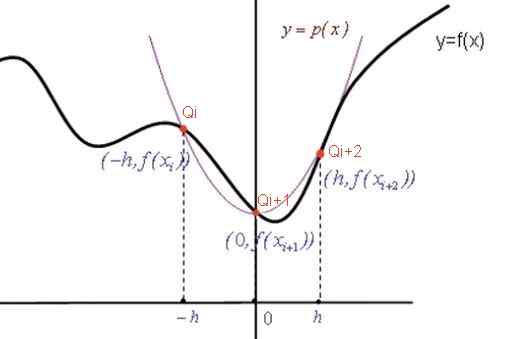Obrázok 2. Graf na demonštráciu vzorca Simpson. Zdroj: f. Zapata.

Interpolačné polynomické koeficienty

Parabola rovnica p (x) má všeobecnú formu: p (x) = a x² + B X + C. Keď podobenstvo prechádza bodmi, ktoré sú označené červenou farbou (pozri obrázok), potom sú koeficienty A, B, C určené z nasledujúceho systému rovníc:

A (-H)² - B h + c = f (xi)

C = f (xi+1)

A (h)² + B h + c = f (xi + 2)

Je možné pozorovať, že je určený koeficient C. Aby sme určili koeficient, pridáme prvú a tretiu rovnicu získanie:

2 a h² + 2 C = f (xi) + f (xi + 2).

Potom sa vymení hodnota C a je jasná:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

Aby sa určil koeficient B, tretia rovnica prvej sa odpočítava a B sa zbavuje:

B = [f (xi+2) - f (xi)] = 2 h.

Stručne povedané, polynóm druhého stupňa P (x), ktorý prechádza bodmi Qi, Qi+1 a Qi+2, má koeficienty:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

B = [f (xi+2) - f (xi)] = 2 h

C = f (xi+1)

Výpočet približného integrálu v [xi, xi+2]

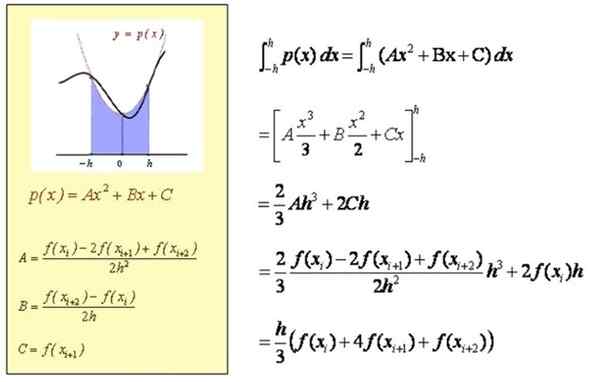
Približný výpočet integrálu v [a, b]

Ako už bolo povedané, v celkovom intervale integrácie [a, b] oddielu x0, x1, x2,…, xn -1, xn s krokom H = xi+1 - xi = (b - (b -) / n, kde n je pár.

Môže vám slúžiť: Chyba vzorkovania: vzorce a rovnice, výpočet, príklady

Potom integrál definovaný v celkovom intervale [a, b] je súčet integrálov v subintervaloch [xi, xi+2], ktoré sa priblížia integrálmi interpolačných polynómov p (x):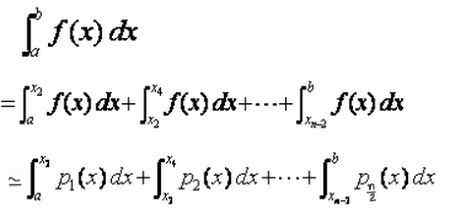

V predchádzajúcej časti sa zistil vzorec polynómových integrálov v subintervaloch. Uplatňovanie tohto výsledku na každý integrál, ktorý má: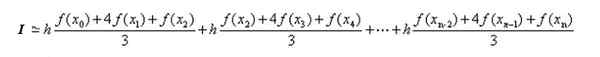

Ktoré je možné prepísať kompaktnejším spôsobom nasledovne: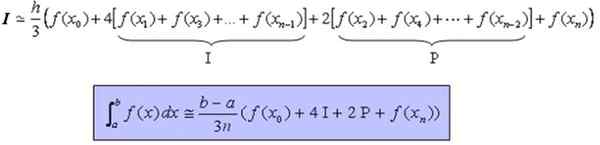

Priblíženie

Ak funkcia, do ktorej sa chcete integrovať do intervalu [a, b], sa odvodila do štvrtého rádu, kontinuálneho v tomto intervale, potom je možné nájsť vzorec, ktorý umožňuje určiť maximálnu úroveň chýb v prístupe z Simpson Sn vzorec Pre hodnotu integrálu: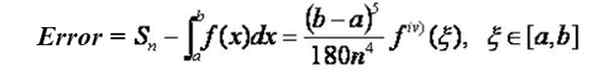

Upozorňujeme, že chyba klesá so štvrtým výkonom číslo intervalu. Napríklad, ak prejdete z N -subdivízií na 2N, potom sa chyba zníži o 1/16 faktor.

Horná úroveň chýb získaná pri prístupe Simpson sa dá získať z toho istého vzorca, čím nahradí štvrtý derivát maximálnou absolútnou hodnotou štvrtého derivátu v intervale [a, b].

Vyriešené príklady

- Príklad 1

Zvážte funkciu f (x) = 1 / (1 + x²). 

Nájdite definovaný integrál funkcie F (x) v intervale [-1, 1] pomocou metódy Simpson s dvoma pododdielmi (n = 2).

Riešenie 

Sa berie n = 2. Limity integrácie sú a = -1 a b = -2, potom je oddiel ako tento: 

X0 = -1; X1 = 0 a x2 = +1.

Preto si Simpsonov vzorec prijíma nasledovne:

S n = 2 → xo = -1, x1 = 0; x2 = 1, preto:

- Príklad 2

Zvážte funkciu f (x) = 1 / (1 + x²). 

Nájdite definovaný integrál funkcie F (x) v intervale [-1, 1] pomocou Simpsonovho vzorca so štyrmi pododdielmi (n = 4).

Môže vám slúžiť: odhad prostredníctvom intervalov

Riešenie 

Sa berie n = 4. Limity integrácie sú a = -1 a b = -2, potom je oddiel ako tento: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 a x4 = +1.

Simpsonov vzorec je stanovený takto:

Integral ≃ [(b -a)/(3 n)] [F (x0) + 4 i + 2 p + f (xn)]

V prípade, že sa používa, je to nasledovne:

Integral ≃ (1- (1))/(3⋅4)] [F (-1) + 4 [F (-½) + F (½)] + 2 [F (0)] + F (1)

Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2 šhlý + ½] = (⅙) [47/5] = 47/30 = 1,5666

- Príklad 3

Určte definovaný integrál predchádzajúcich príkladov presne a urobte porovnanie presného výsledku s výsledkami získanými Simpsonovou vzorcom v príkladoch 1A a 1B.

Riešenie 

Neurčitý integrál funkcie f (x) = 1 / (1 + x²) je funkcia Arktan (x).

Pri hodnotení limitov integrácie:

Integral = Arctan (1) - Arctan (-1) = π/4 - (-π/4) = π/2 = 1 5708

Ak porovnáme výsledok presného riešenia s riešením získaným metódou Simpson s n = 2 a n = 4, ktoré máme:

Pre n = 2 rozdiel medzi presným a približným roztokom je π/2 -5/3 = -0959, to znamená percentuálny rozdiel -0,06%.

A pre prístup Simpson s n = 4 je rozdiel medzi presným a približným roztokom π/2 - 47/30 = 0,0041, to znamená percentuálny rozdiel 0,003%.

Navrhované cvičenie

Simpsonova metóda je vhodná na použitie v programovacích jazykoch a počítačových aplikáciách zameraných na matematické výpočty. Navrhuje sa čitateľovi, ktorý na základe vzorcov uvedených v tomto článku napísal svoj vlastný kód do svojho obľúbeného programu.

Nasledujúci obrázok ukazuje cvičenie, v ktorom bol vzorec Simpson implementovaný v Štúdio Smath, Zadarmo softvér dostupný pre operačné systémy Okná a Android.

Obrázok 3. Príklad numerickej integrácie prostredníctvom pravidla Simpson pomocou softvéru. Zdroj: f. Zapata.

Odkazy

1. Casteleiro, J. M. 2002. Komplexný výpočet (ilustrované vydanie). Madrid: ESIC Editorial.
2. UPV. Metóda Simpsona. polytechnická univerzita vo Valencii. Obnovené z: YouTube.com
3. Purcell, e. 2007. Výpočet deviateho vydania. Sála.
4. Wikipedia. Pravidlo Simpson. Obnovené z: je.Wikipedia.com
5. Wikipedia. Lagrange polynomiálna interpolácia. Obnovené z: je.Wikipedia.com