Čo sú algebraické výrazy a ktoré sú najčastejšie?

Ten algebraické výrazy Sú to matematické výrazy, ktoré obsahujú čísla a písmená. V kombinácii so symbolmi matematických operácií umožňujú získanie vzorcov alebo rovníc z opisov, ktoré sa uskutočnili slovami. 

Tieto písmená môžu zase pridať, odpočítať, vynásobené alebo vydelené inými číslami, ktoré môžu byť explicitné alebo tiež reprezentované písmenami.

postava 1. Príklady algebraických výrazov

[TOC]

Na čo sú algebraické výrazy?

Napríklad výraz:

2x + 3 

Je to algebraický výraz, kde písmeno „x“ predstavuje číslo možno neznáme alebo ktoré môže mať rôzne hodnoty.

Aká je výhoda použitia algebraického výrazu namiesto toho, aby hovorí: „Dvojnásobné číslo pridané do 3“?

Po prvé, algebraický výraz zaberá menej priestoru. A potom, ak X nie je pevné číslo, môžu sa „x“ poskytnúť rôzne hodnoty, aby sa získali rôzne výsledky tohto výrazu.

Toto je známe ako numerická hodnota algebraického výrazu.

Napríklad, ak x = 1, výsledok je 22 + 3 = 2 + 3 = 5

Namiesto toho, keď urobíte x = -2, sa prejaví expresia 2,2 (-2) + 3 = -4 + 3 = -1

V inom type aplikácie predstavujú algebraické výrazy rovnicu alebo rovnosť, ktorá je potrebné vyriešiť, aby poznala hodnotu čísla predstavovaného listom.

Tu máme jednoduchú lineárnu rovnicu:

2⋅x + 3 = 7

Riešenie tejto rovnice, ktorá je mimochodom tiež algebraickým výrazom, je:

x = 2

Pretože vynásobenie 2 o 2 dáva 4 plus 3, dáva výsledok: 7. Ale je ľahšie pochopiť, kedy sa používa algebraický výraz namiesto toho, aby opisoval všetko slovami.

Najčastejšie algebraické výrazy

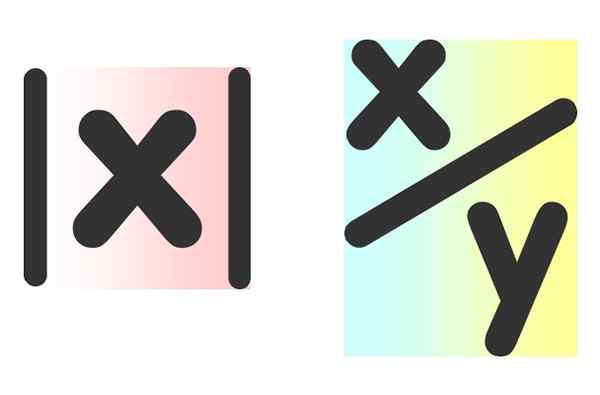Obrázok 2. Neznáme sumy často symbolizujú písmená „x“ a „y“. Vľavo je absolútna hodnota čísla a napravo kvocient v dvoch číslach. Zdroj: Pixabay.

Algebraické výrazy sa široko používajú v matematike, vede, hospodárstve a správe.

Nižšie je uvedený zoznam výrazov, ktoré sa objavujú veľmi často v matematike a iných predmetoch, v ktorých sa požaduje alebo vyrieši návrh.

Môže vám slúžiť: obvod kruhu: Ako ho vytiahnuť a vzorce, vyriešené cvičenia

Zvyčajne sa neznáme alebo neznáme číslo označuje ako „x“, ale môžeme použiť akýkoľvek iný abecedný list podľa dohody.

Malo by sa tiež pamätať na to, že v algebraickom výraze to môže zahŕňať viac ako jednu hodnotu, neznáme alebo premennú, takže každému z nich by malo byť pridelené iné písmeno.

Zoznam algebraických výrazov

-Dvojnásobok alebo dvojnásobok čísla: 2x

-Duple čísla ďalších jednotiek: 2m + 3

-Tretia časť čísla: Z/3

-Dvojnásobok čísla okrem jeho tretej časti: 2x - x/3

-Štvorec čísla: x²

-Štvorec čísla toho viac tohto čísla: x² + 2x

-Duple štvorca čísla: 2x²

-Číslo krútiaceho momentu: 2n

-Nepárne číslo: 2n + 1

-Tri po sebe idúce čísla: x, (x+1), (x+2)

-Tri po sebe idúce rovnomerné čísla: 2n, 2n +2, 2n +4

-Tri po sebe idúce nepárne čísla, 2n + 1, 2n + 3, 2n + 5

-Určité číslo pridané do jeho po sebe nasledujúceho: x +(x +1) = 2x +1

-Polovica po sebe idúce celého čísla: (x+1)/2

-Trojnásobok polovice štvorca čísla: 3. (1/2) x² = (3/2) x²

-Polovica jedného ďalšieho počtu ďalších: x/2 + y/3

-Tretia časť produktu medzi štvorcom čísla a iným číslom, ku ktorému bola jednotka odpočítaná: (1/3) x².(Y-1)

-Číslo a jeho opak: a, -a

-Číslo a jeho inverzné: a, 1/a

-Súčet čísla s po sebe idúcim zvýšeným na štvorec: x + (x + 1)²

-Odpočítajte 7 s dvojnásobkom určitého počtu vysokých na štvorec: (2x)² - 7

-Dve čísla, ktoré pri vynásobení dávajú 24: P.Q = 24

Môže vám slúžiť: uhlové posunutie

-Absolútna hodnota čísla: │x│

-Kvocient medzi dvoma číslami: x/y

-Druhý koreň produktu dvoch čísel: √x.a

Obrázok 3. Tento algebraický výraz sa číta ako „druhý koreň produktu dvoch čísel x a y“. Zdroj: Pixabay.

-Jedno číslo, ktoré presahuje druhé v 30 jednotkách: x = y +30

-Dvojnásobok čísla, na ktoré sa jeho polovica odpočíta: 2x-x/2

Verbálne problémy a ich algebraické výrazy

- Problém 1

Polovica kravy váži 100 kg viac ako váži štvrtinu tej istej kravy. Koľko váži krava?

Odpoveď

Pre algebraické vyjadrenie tohto problému nazývame X hmotnosť kravy.

Polovica kravy váži ½ x. Štvrtá časť kravy váži ¼ x. Nakoniec algebraický výraz zodpovedajúci: „Polovica kravy váži 100 kg viac ako štvrťrok“ je:

½ x = ¼ x + 100

Ak chcete vedieť, koľko krava váži, musíte zoskupovať podmienky s X na ľavej strane a nechať 100 doprava:

(½ -¼) x = 100

¼x = 100

x = 400 kg

Krava váži 400 kg.

- Problém 2

Na farme je počet králikov dvakrát toľko kráv. Ak je počet kráv 10. Koľko je tam králikov?

Odpoveď

Ak C je počet králikov a V je počet kráv, potom algebraický výraz vyhlásenia je:

C = 2 štúp

V = 10

Nahradenie hodnoty V v prvej z rovníc, ktoré sa získa:

C = 2 ⋅ 10 = 20

To znamená, že farma má dvadsať králikov.

- Problém 3

Aké je číslo vynásobené siedmimi a odpočítať šesť, dáva dvadsať -?

Odpoveď

Ak nazývame toto neznáme číslo X, je možné zvýšiť tento algebraický výraz:

Môže vám slúžiť: Asociatívna vlastnosť: Sum, násobenie, príklady, cvičenia

7x - 6 = 29

Na 6. ľavej strane prechádza na pravú stranu rovnosti so zmeneným znakom:

7x = 29 + 6 = 35

Z toho vyplýva, že x = 35/7 = 5

- Problém 4

Dvojnásobok určitého čísla 13 sa odpočíta a 7 je 7. Aké je číslo?

Odpoveď

Ak zavoláme toto číslo X, potom jej algebraická rovnica je:

2 x - 13 = 7

Aká je hodnota 2x ?

Odpoveď je, že 2x musí byť (13 + 7), takže keď odstránite 13, je 7.

To znamená, že 2x sa musí rovnať 20, to znamená:

2x = 20

Číslo X, ktoré vynásobené 2 DA 20, je 10, preto:

x = 10

- Problém 5

Dve po sebe idúce celé čísla sčítajú 23. Navrhnúť algebraickú rovnicu, ktorá umožňuje určiť číslo a nájsť ju.

Odpoveď

Predpokladajme, že prvé z čísel je n, takže ten, ktorý nasleduje, je n+1 a súčet týchto dvoch je n+(n+1). Je tiež známe, že súčet sumy je 23, potom je napísaná rovnica:

n + (n + 1) = 23

Riešenie sa získa najprv zjednodušuje ľavú stranu rovnosti:

2 n + 1 = 23

Potom 2 N je vymazaný 1 na pravý člen so zmeneným znakom:

2 n = 23 - 1

Správny člen je vyriešený:

2 n = 22

Ďalej, n, odovzdanie 2, ktoré vynásobia člena ľavice, ktorý vydelí člena pravice:

N = 22/2

A konečný výsledok sa získa:

N = 11

Odkazy

1. Baldor, a. Algebra. Stredoamerický kultúrny úvodník C.Do.
2. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
3. Cimanet. Algebraické výrazy. Získané z: CinAmet.Uoc.Edu
4. Guzman P. Algebraické výrazy. Zdroj:: Koncept konečného obdobia.z
5. Kvíz. Algebraické výrazy. Uzdravené z: možno.Utrpenie.Edu
6. Martha. Príklady algebraických výrazov. Obnovené z: Superprof.je