Čo sú trojuholníkové čísla? Vlastnosti a demonštrácie

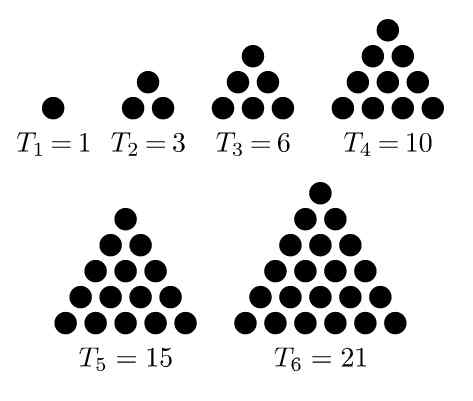
Je to známe ako trojuholník do sekvencie čísel, ktoré sa získajú pomocou usporiadania alebo čísla bodov rovnostranného trojuholníka. Prvá zo sekvencií je: 1, 3, 6, 10, 15, 21, ..

Prvý trojuholníkový problém je 1, druhý je 3, pretože sa získa z pridania dvojfo -bodového riadku k predchádzajúcemu, aby sa vytvoril rovnostranný trojuholník troch prvkov.

postava 1. Sekvencia prvých šiestich trojuholníkových čísel. Zdroj: Wikimedia Commons. Melchoir/CC By-SA (https: // creativicecommons.Org/licencie/By-SA/3.0)

Tretia je 6, ktorá sa objaví pri pridávaní trojfointu riadku k predchádzajúcemu usporiadaniu, takže na stranu sa vytvorí trojuholníkový trojuholník. 10 sekvencií sa získa pridaním ďalšieho riadku k predchádzajúcemu usporiadaniu tak, aby sa na stranu vytvoril trojuholník so štyrmi bodmi.

Vzorec, ktorý vám umožňuje nájsť prvok n Z trojuholníkovej sekvencie je známe predné trojuholníkové číslo:

Tón_n = T_N-1 + n

Zoznam prvých šiestich trojuholníkových čísel sa dosiahne takto:

-najprv: 1

-Druhý: 1 + 2 = 3

-Tretiny: (1 +2) + 3 = 3 + 3 = 6

-Izba: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Piaty: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Šiesty: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

[TOC]

Vlastnosti trojuholníkových čísel

1.- N-simo TN trojuholníkové číslo sekvencie trojuholníkových čísel je polovica n vynásobená n+1:

Tón_n = ½ n (n+1)

2.- Súčet trojuholníkového čísla n-ésimo s predným trojuholníkom, to znamená (n-1) -sheimo, je vyvýšený štvorcový:

Tón_n + Tón_N-1= n²

3.- Rozdiel v trojuholníkovom čísle n-menej trojuholníkovo N-ésimo nižší je n:

Tón_n - Tón_N-1 = n

4.- Súčet prvých trojuholníkových čísel sa nazýva tetraedrálne číslo SN a rovná sa šiestej časti produktu vynásobenej (n + 1) a vynásobená (n + 2):

Môže vám slúžiť: zdaňovanie

Siež_n= ⅙ n (n + 1) (n + 2)

5.- Každé prirodzené číslo n je výsledkom súčtu troch trojuholníkových čísel:

N = A1 + A1 + A3

Tento posledný majetok alebo veta objavil veľký matematik Carl Friedrich Gauss v roku 1796, ktorý skóroval vo svojom denníku umiestnením gréckeho obdivu Eureka! čo to znamená „Dosiahol som to“.

To bolo to isté slovo, ktoré už oveľa skôr používali grécky Archimedes, keď určil zjavnú váhu ponoreného tela.

V tomto vzťahu sa nulové číslo považuje za trojuholníkový a môže dôjsť k opakovaniu.

Demonštrácia

- Demonštrácia 1

Dokážte, že trojuholníkové číslo n-Toto je:

Tón_n = ½ n (n+1)

Je ľahké odvodiť predchádzajúci vzorec, ak si uvedomíme, že do trojuholníkového usporiadania môžeme pridať rovnaký počet bodov, aby sme vytvorili štvornásobné body.

Ako celkový počet bodov usporiadania vo forme štvornásobného je počet riadkov n vynásobené počtom stĺpcov (N+1), Potom trojuholníkové usporiadanie bude mať iba polovicu bodov usporiadania vo forme štvornásobného.

Tu je znázornené na obrázku 2.

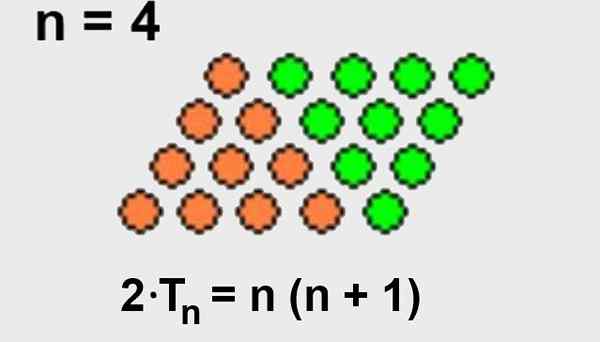Obrázok 2. Usporiadanie štvorcového tvaru, v ktorom celkový počet bodov je počet riadkov n vynásobených počtom stĺpcov n+1. Celkový počet bodov je tiež dvakrát väčší ako v trojuholníkovom usporiadaní. Zdroj: Wikimedia Commons.

- Demonštrácia 2

Preukázať, že suma n-Toto trojuholníkové číslo s n-Menej jeden trojuholníkové číslo je n na druhej strane:

Tón_n + Tón_N-1= n²

Už sa ukázalo, že trojuholníkové číslo n-Toto je dané:

Tón_n= ½ n (n+1)

Preto je predné trojuholníkové číslo:

Tón_N-1 = ½ (n-1) ((n-1) + 1) = ½ n (n-1)

Súčet oboch zvyškov:

Tón_n + Tón_N-1 = ½ n (n + 1) + ½ n (n - 1)

½ N sa berie na získanie:

Tón_n + Tón_N-1 = ½ n [(n + 1) + (n - 1) = ½ n [n + 1 + n - 1]

A okamžite sa výraz zjednoduší vo vnútri konzoly:

Môže vám slúžiť: odhad prostredníctvom intervalov

Tón_n + Tón_N-1 = ½ n [2 n] = ½ 2 n ⋅ n

Teraz si pamätajte, že ½ pre 2 je 1 a že n pre n je N Square, máte:

Tón_n + Tón_N-1 = n²

Túto vlastnosť sa dá demonštrovať aj geometricky, trojuholník je jednoducho dokončený za vytvorenie štvorca, ako je znázornené na obrázku 3.

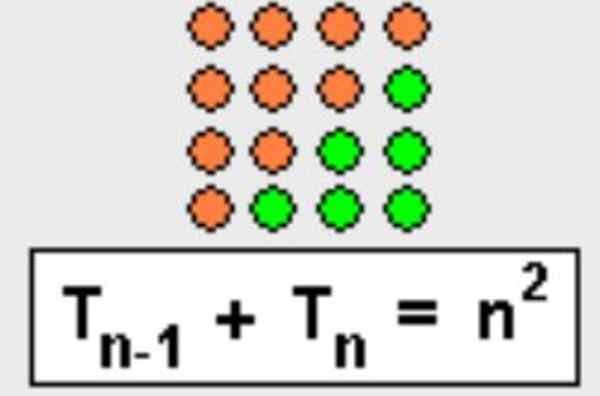Obrázok 3. Súčet N-ésimo trojuholníkového čísla s predným trojuholníkom sa rovná N-štvorca. Zdroj: Wikimedia Commons.

- Demonštrácia 3

Rozdiel v trojuholníkovom počte objednávok n mínus trojuholníkový počet objednávok N-1 je n:

Tón_n - Tón_N-1 = n

Toto je možné otestovať jednoducho tak, že si uvedomíte, že nasledujúce trojuholníkový počet sa získa z predchádzajúceho vzorca:

Tón_n = T_N-1 + n

A odtiaľ je zrejmé, že Tón_n - Tón_N-1 = n. Graficky je tiež ľahké vizualizovať, ako je znázornené na obrázku 4.

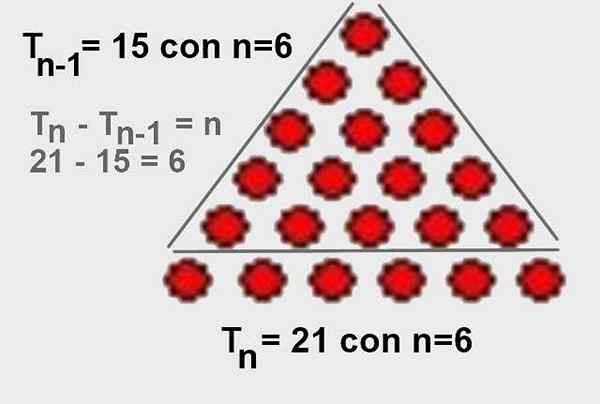Obrázok 4. Rozdiel trojuholníkového počtu rádov n menej predný trojuholník poradie n-1 je n. Zdroj: Wikimedia Commons.

- Demonštrácia 5

Súčet prvých trojuholníkových čísel sn Rovná sa šiestej časti produktu vynásobenej (n + 1) a vynásobená (n + 2):

Siež_n = ⅙ n (n + 1) (n + 2)

Použime trojuholníkový počet objednávok n: Tón_n= ½ n (n+1). Súčet prvého n Trojuholníkové čísla to označujú za Siež_n  

Napríklad, Siež₁ znamená súčet prvého trojuholníkového vydania, ktoré bude nepochybne 1.

Potom sa pozrime, či je vzorec, ktorý sa snažíme vyskúšať, dodržiava n = 1:

Siež₁ = ⅙ 1ple22 = 1

V skutočnosti sa skontroluje vzorec pre n = 1. Je ľahké vizualizovať, že súčet prvých trojuholníkových čísel N+1 bude súčtom prvého N Viac v nasledujúcom trojuholníkovom čísle:

Siež_N+1 = S_n + Tón_N+1

Teraz predpokladajme vzorec Siež_n Je splnený pre n, potom ho nahradíme v predchádzajúcom výraze a pridáme trojuholníkový počet objednávok N+1:

Siež_N+1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]

Môže vám slúžiť: kolmá línia: Charakteristiky, príklady, cvičenia

Pozrime sa krok za krokom, čo sa získa:

-Vykonávame súčet dvoch frakčných výrazov:

Siež_N+1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] /12 

-Odstráni sa z čitateľa spoločného na 2 (n + 1) (n + 2) a zjednodušuje:

Siež_N+1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Predchádzajúci výsledok súhlasí s vzorcom Sn Ak sa vymení n+1, čo bolo preukázané indukciou vzorec súčtu prvých trojuholníkových výrazov.

Tetraedrálne číslo

Získaný výsledok sa volá Tetraedrický počet objednávok n, Pretože je to ako akumulácia trojuholníkových vrstiev, ktoré tvoria tetrahedron, ako je to znázornené v nasledujúcej animácii.

Obrázok 5. Súčet N trojuholníkových čísel zodpovedá stohu vrstiev N, N-1, ..., 1 trojuholníkov, ktoré tvoria pravidelný tetrahedron. Zdroj: Wikimedia Commons.

Odkazy

1. Camacho J. Neočakávaný vzhľad trojuholníkových čísel. Získané z: Masscience.com
2. Claudio. Trojuholník. Obnovené z: jednoducho čísla. Blog. com
3. Wikipedia. Trojuholník. Obnovené z: je.Wikipedia.com
4. Wikipedia. Trojuholník. Zdroj: In.Wikipedia.com
5. Wikipedia. Číslo Tretramedrálne. Zdroj: In.Wikipedia.com