Čo je dynamická rovnováha? (S príkladom)

On dynamická rovnováha Je to stav, v ktorom je mobilný objekt ideálne znázornený ako častica, keď je jeho pohyb rovnomerný priamy. Tento jav sa vyskytuje, keď je zrušený súčet externých síl konajúcich na ňom.

Zvyčajne sa verí, že ak neexistuje žiadna sieť alebo výsledná sila na objekt, odpočinok je jediným možným dôsledkom. Alebo tiež, že pre telo bude v rovnováhe, nemala by existovať žiadna sila.

postava 1. Táto mačka sa pohybuje v dynamickej rovnováhe, ak to robí konštantnou rýchlosťou. Zdroj: Pixabay.

V skutočnosti je rovnováha absencia zrýchlenia, a preto je konštantná rýchlosť úplne možná. Mačka na obrázku sa môže pohybovať bez zrýchlenia.

Objekt, ktorý má rovnomerný kruhový pohyb, nie je v dynamickej rovnováhe. Aj keď je jeho rýchlosť konštantná, existuje zrýchlenie smerované do stredu obvodu, ktoré ju udržuje v trajektórii. Toto zrýchlenie je zodpovedné za správne zmenu na rýchlostný vektor.

Nulová rýchlosť je osobitnou situáciou rovnováhy častíc, čo zodpovedá potvrdeniu, že objekt je v pokoji.

Pokiaľ ide o zvažovanie objektov za častice, je to veľmi užitočná idealizácia pri opise ich globálneho pohybu. Mobilné objekty, ktoré nás obklopujú, sa v skutočnosti skladajú z veľkého počtu častíc, ktorých individuálna štúdia by bola ťažkopádna.

[TOC]

Princíp superpozície

Tento princíp umožňuje nahradiť pôsobenie viacerých síl na objekte s ekvivalentom nazývaným výsledná sila studená alebo sieťová sila FN a v tomto prípade je neplatné:

F1 +F2 +F3 +… . = FR = 0

Kde sily f1, f2, f3 .. ., Fi sú rôzne sily, ktoré pôsobia na tele. Sumory notácia je kompaktný spôsob jeho vyjadrenia:

Pokiaľ nevyvážená sila nezasahuje, objekt sa dá udržať neurčito pohybovať sa konštantnou rýchlosťou, pretože táto panoráma môže zmeniť iba sila.

Pokiaľ ide o komponenty výslednej sily, dynamický rovnovážny stav častice je vyjadrený nasledovne: fx = 0; FY = 0; FZ = 0.

Rotácia a rovnováha

Pre model častíc je podmienka FR = 0 dostatočná záruka rovnováhy. Ak však vezmeme do úvahy rozmery študovaného mobilného mobilného telefónu, existuje možnosť, že objekt sa môže otočiť.

Hnutie rotácie znamená existenciu zrýchlenia, preto rotujúce telá nie sú v dynamickej rovnováhe. Otočenie tela potrebuje nielen účasť sily, ale je potrebné uplatniť vhodné miesto.

Ak to chcete skontrolovať, môžete na povrch bez trenia položiť tenkú tyč s dĺžkou, napríklad ľadový povrch alebo veľmi leštené zrkadlo alebo sklo. Normálne zostatky na váhu vertikálne a pri nanášaní dvoch síl F1 a F2 rovnakej veľkosti, podľa diagramu nasledujúceho obrázku, čo sa stane:

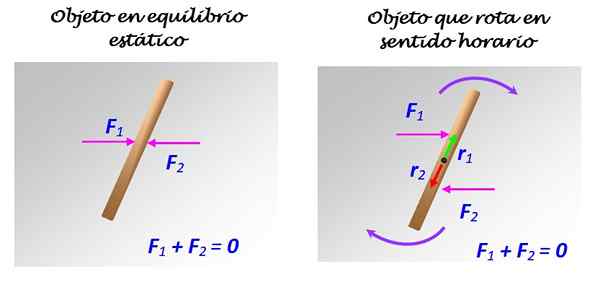Obrázok 2. Tyč na povrchu bez trenia môže alebo nemusí byť v rovnováhe, v závislosti od toho, ako sa aplikujú sily 1 a 2. Zdroj: Self Made.

Ak sa F1 a F2 použijú, ako je to znázornené vľavo, so spoločnou líniou akcie, tyč zostane v pokoji. Ale ak sa F1 a F2 uplatňujú, ako je znázornené vpravo, s rôznymi riadkami pôsobenia, aj keď sú rovnobežné, sa rotácia vyskytuje v pláne, okolo osi, ktorá prechádza stredom.

V tomto prípade F1 a F2 tvoria niekoľko síl alebo jednoducho pár.

Krútiaci moment alebo moment sily

Účinkom krútiaceho momentu je vytvorenie rotácie na predĺžený objekt, ako je napríklad ukážka tyče. Vektorová veľkosť je nazývaná krútiacim momentom alebo tiež okamihom sily. Označuje sa ako τ a vypočíta sa podľa:

τ = r x f

V tomto výraze f je aplikovaná sila a R je vektor, ktorý prechádza z osi rotácie do bodu použitia sily (pozri obrázok 2). Smer τ je vždy kolmý na rovinu, kde ležia f a r a jeho jednotky v medzinárodnom systéme sú n.m.

Napríklad smer momentov vytvorených F1 a F2 je smerom k papieru podľa pravidiel vektorového produktu.

Aj keď sily sa navzájom rušia, ich krútiace momenty nie. A výsledkom je uvedená rotácia.

Rovnovážne podmienky pre rozšírený objekt

Toto sú dve podmienky, ktoré musia byť splnené, aby sa zaručil zostatok rozšíreného objektu:

Vyriešený príklad

Máte zásuvku alebo kmeň, ktorý váži 16 kg-f, ktorý sa prechádza cez naklonenú rovinu s konštantnou rýchlosťou. Uhol sklonu klinu je 9 = 36 °. Odpoveď:

a) Aká je veľkosť dynamickej trenia, ktorá je potrebná na to, aby sa kmeň skĺzol konštantnou rýchlosťou?

b) Koľko stojí koeficient kinetického trenia?

c) Ak je výška H naklonenej roviny 3 metre, nájdite rýchlosť zostupu kmeňa s vedomím, že dosiahnutie zeme trvá 4 sekundy.

Riešenie

Kmeň môže byť ošetrený tak, akoby to bola častica. Preto sa sily budú uplatňovať v bode, ktorý sa nachádza približne v jeho strede, na ktorom je možné predpokladať všetku jej hmotnosť. Do tohto bodu bude sledovaná trať.

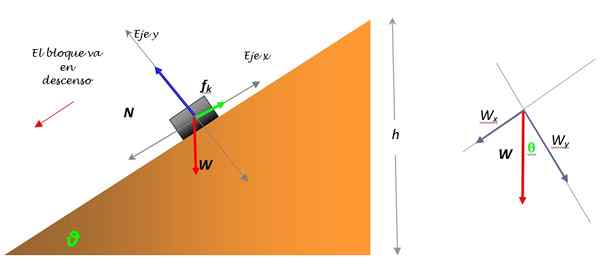Obrázok 3. Diagram voľného tela pre kmeň, ktorý skĺzne z kopca a rozklad hmotnosti (vpravo). Zdroj: Self Made.

Hmotnosť w je jediná sila, ktorá nespadá na jednu z súradnicových osí a musí byť rozdelená na dve komponenty: WX a WY. Tento rozklad je uvedený v schéme (obrázok 3).

Je tiež vhodné odovzdať hmotnosť jednotiek medzinárodného systému, pre ktoré stačí vynásobiť 9.8:

Wy = w.cosθ = 16 x 9.8 x cos 36 ° n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x Sin 36 ° = 92.2 n

Oddiel a

V celej horizontálnej osi sú horizontálna zložka hmotnosti WX a dynamická alebo kinetická trenie FK, ktorá je proti pohybu, ktorá je proti pohybu.

Výber pozitívneho zmyslu v smere pohybu je ľahké si všimnúť, že je WX zodpovedný za blok, aby šiel z kopca z kopca. A keď je trenie proti, namiesto rýchleho skĺznutia má blok možnosť neustáleho kĺzania z kopca z kopca.

Prvá rovnovážna podmienka je dostatočná, pretože kmeň zaobchádzame ako s časticou, ktorá je zabezpečená vo vyhlásení, ktoré je v dynamickej rovnováhe:

Wx - fk = 0 (na horizontálnej adrese nie je žiadne zrýchlenie)

FK = 92.2 n

Oddiel B

Veľkosť dynamického trenia je konštantná a je daná fk = μk n. To znamená, že dynamická trecia sila je úmerná normálu a je potrebné poznať koeficient trenia.

Pri pozorovaní diagramu voľného tela je zrejmé, že na vertikálnej osi máme normálnu silu n, ktorú klin vyvíja na kmeň a je nasmerovaný nahor. Je vyvážená vertikálnou zložkou hmotnosti wy. Výber ako pozitívny zmysel a využívanie Newtonovho druhého zákona a výsledky stavu rovnováhy:

N - wy = 0 (nedochádza k pohybu pozdĺž vertikálnej osi)

Preto:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2/126.9 = 0.73

Oddiel C

Celková vzdialenosť prevezená kmeňom od vrcholu klinu po zem sa nachádza trigonometriou:

d = h/sin 36 ° = 3/sin 36 ° m = 5.1 m.

Na výpočet rýchlosti sa používa definícia rovnomerného priameho pohybu:

V = d/t = 5.1 m/4 s = 1.3 m/s

Odkazy

1. Rex, a. 2011. Základy fyziky. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa. 120 - 124.
3. Serway, r., Vulle, C. 2011. Základy fyziky. 9NA ED. Učenie sa. 99-112.
4. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. Kopec MacGraw. 71 - 87.
5. Walker, J. 2010. Fyzika. Addison Wesley. 148-164.