Testovanie hypotéz

Čo je test hypotézy?

Ten testovanie hypotéz, V štatistike je to postup, ktorý sa používa na kontrolu, ako úspešná je dohad o a populácia. Tieto domnienky sa volajú hypotéza, že sa v zásade považujú.

Tento dôkaz poskytuje údaje o vzorke, tie, ktoré pochádzajú z významnej časti populácie, nazývané vzorka. Teória pravdepodobností poskytuje potrebné techniky na porovnanie pravdivosti hypotéz.

Príklady hypotéz sú:

-Priemerná teplota ľudského tela je 36.1 ° C.

-V priemere slaná arašidová taška vyrobená v továrni na občerstvenie váži 50 g.

-80% obyvateľov mesta, uskutočnili nákupy online za posledných 6 mesiacov.

-Skóre testov IQ pre študentov vysokých škôl zo známeho inštitúcie má štandardnú odchýlku 15.

-Určitá náhodná premenná X sleduje Poissonov rozdelenie.

Prvé štyri sú typu hypotézy parametrický, Pretože ide o vyhlásenia o niektorých parametroch populácie, ako je priemerná, štandardná odchýlka alebo určitý pomer.

Na druhej strane posledná hypotéza stanovuje rozdelenie náhodnej premennej a keďže sa netýka žiadneho parametra alebo vlastnosti populácie, hovorí sa, že ide o hypotézu nie parametrický.

Nulová hypotéza a alternatívna hypotéza

Existujú dva druhy hypotézy, s ktorou sa môžu vykonať test, ktorý bude slúžiť na ich kontrast:

-Nulová hypotéza, označený ako h₀, uvádza, že študovaný parameter má zavedenú hodnotu alebo že náhodná premenná sleduje určité rozdelenie. Preto symbolickým vyjadrením nulovej hypotézy sa vždy používa symbol rovnosti.

-Alternatívna hypotéza: volá H₁, Potvrdzuje, že parameter alebo distribúcia sa líšia od toho, čo nulová hypotéza zaisťuje, a preto symbolicky vyjadruje alternatívnu hypotézu, symboly sa používajú: alebo ≠, ale nikdy rovnosť.

Môže vám slúžiť: Vlastnosť algebra zámku: demonštrácia, príklady

Ak je akceptovaná nulová hypotéza, alternatívna hypotéza je odmietnutá, takže obidve sa vzájomne vylučujú.

Významnosť

Je to opatrenie pre chybu, ktorú je možné urobiť pri vykonávaní testu hypotézy. Je definovaná ako pravdepodobnosť odmietnutia nulovej hypotézy, pretože je pravda. Zvyčajne sa označuje gréckym písmenom α:

a = p (odmietnuť h₀ Keď je to pravda)

Hodnoty bežne používané pre a sú 0.01, 0.05 a 0.10; byť druhým najčastejším použitím. Rovnocenné s 1%, 5% a 10% pravdepodobnosť, že urobia chyby pri odmietnutí h₀, Ale v každom prípade, čím nižšia je úroveň významnosti, tým spoľahlivejší výsledok testu.

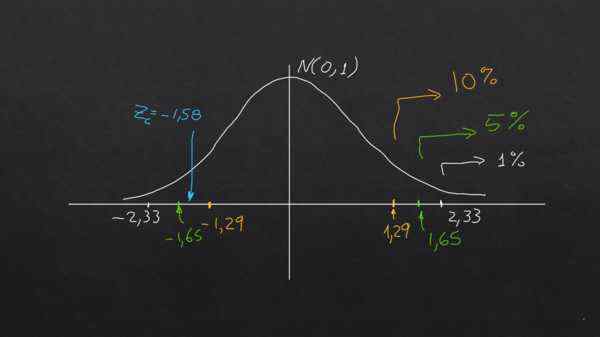
Hodnota alfa (a) sa dá chápať ako percentuálna frakcia pravého chvosta (alebo ľavého) oblasti v normálnom distribúcii (μ = 0 a σ = 1) a tieto hodnoty sa vždy vyskytujú pri z = 2,33 pre a = 0.01; pri z = 1,65 pre a = 1,65 a pri z = 1,29 pre a = 0,1.

Kroky na vykonanie testu hypotézy

Krok 1

Definujte nulové a alternatívne hypotézy. Nulová hypotéza ukazuje, že študovaný parameter, nazývaný 9, sa rovná referenčnej hodnote, označovanú ako 9₀:

H₀: 9 = 9₀

Napríklad, ak sa skúmajú účinky lieku na určitú charakteristiku populácie laboratórnych myší, nulová hypotéza predpokladá, že tento liek nezmení v takejto charakteristike a že to má konštantnú hodnotu 9₀.

Na symbolizáciu nulovej hypotézy sa na druhej strane vždy používa znak rovnosti, alternatívna hypotéza využíva jeden zo symbolov alebo ≠.

V príklade liečiva alternatívna hypotéza ukazuje, že zlúčenina má určitý vplyv na danú charakteristiku. Preto je to väčšie, nižšie alebo jednoducho odlišné od referenčnej hodnoty 9₀.

Môže vám slúžiť: faktorové notácie: Koncept, príklady a cvičenia

Krok 2

Vyberte si primeranú úroveň významnosti, ktorá sa zvyčajne stanoví na 5 %, ako už bolo uvedené.

Krok 3

Stanovte populáciu a extrakt z nej vzorky alebo vzorky, ktorých analýza bude slúžiť na kontrast hypotézy a určenie prijatia alebo odmietnutia nulovej hypotézy.

Krok 4

Vyberte a vypočítajte hodnotu štatistiky skúšky pre zhromaždené údaje, z ktorých sa získajú potrebné dôkazy na prijatie rozhodnutia o prijatí alebo odmietnutí nulovej hypotézy. Výber štatistiky skúšky závisí od zvoleného parametra: priemer, odchýlka, pomer alebo iné.

Štatistika pokusu sa získa prevedením parametra vzorky na skóre Z, Štatistiku študenta, R Pearsona alebo Chi Square, podľa vybraného experimentálneho návrhu. Existujú pre to vzorce.

Zvyčajne, ak je parameter populácie priemerom μ, „x bar“ je priemer vzorky, je známa štandardná odchýlka σ a veľkosť vzorky je n> 30, testovacia štatistika Z_C Vypočíta sa so skóre Z:

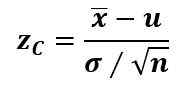
A keď n < 30, pero σ es desconocida, se usa la t de Student.

Krok 5

Stanovte kritériá na prijatie alebo odmietnutie nulovej hypotézy, ktorú je možné vykonať prostredníctvom dvoch postupov:

• Cez hodnoty P.
• V porovnaní s kritickými hodnotami.

Hodnoty P sú ekvivalentné pravdepodobnosti získania zistených výsledkov, pretože nulová hypotéza je pravdivá. Ak sú tieto hodnoty malé, nulová hypotéza je odmietnutá, ak nie, je akceptovaná. V žiadnom prípade hodnoty P nepredstavujú dôkaz, že alternatívna hypotéza je pravdivá.

Malo by sa brať do úvahy, že v teste hypotézy je možné urobiť dva typy chýb:

• Chyba typu I: Odmietnuť h₀ Keď je to pravda. Jeho pravdepodobnosť je a a je rovnocenná s úrovňou dôkazného významu.
• Chyba typu II: Prijať h₀ Keď je to vlastne nepravdivé. Jeho pravdepodobnosť je označená ako β.

Môže vám slúžiť: Aký je vzťah medzi oblasťami Rhombus a obdĺžnik?

Krok 6

Rozhodnite sa prijať alebo odmietnuť nulovú hypotézu. Ak sa použijú hodnoty p, keď P < α, se rechaza H₀ A H je akceptovaný₁, A inak je H akceptovaný₀. Sada hodnôt P < α se conoce como kritická oblasť. Ak je štatistika v tomto intervale, H je odmietnutá₀.

Podobne sa vyberie kritická hodnota podľa vybraného parametra populácie. Ak je to priemer, postupujte takto:

• Test chvosta: 9 < θ₀ alebo 9> 9₀
• Test dvoch chvostov: | θ | < θ₀

Vyriešený príklad

Stroj vyrába skrutky, ktorých nominálna hodnota musí byť dlhá 800 milimetrov, so štandardnou odchýlkou ​​5%.

Odoberie sa náhodná vzorka, tj v rôznych dňoch výrobného týždňa, čo predstavuje asi 40 skrutiek. Ak sa vypočíta priemerná dĺžka vzorky, získa sa hodnota 790 milimetrov.

Určite, či je priemerná dĺžka tolerancie s hladinami významnosti 1%, 5% a 10%.

Riešenie

Prvým je vypočítať priemernú štatistiku testu, ktorá je v tomto prípade odchýlka rozdeleného priemeru medzi štandardnú chybu populácie:

ZC = (790 - 800) / (40 / √40) = -1,58

Kde sa zohľadnilo, že 5% štandardná odchýlka zodpovedá 40 z 800.

Nulová hypotéza je, že priemerná vzorka je v rámci tolerancie povolená na požadovanú úroveň významnosti za predpokladu, že | ZC | je nižšia ako typická hodnota | zt |, inak je nulová hypotéza odmietnutá.

Pre 1% a 5% významnosť je splnená nulová hypotéza, pretože | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Avšak pre 10% význam sa stáva, že | ZC | > 1,29. To znamená, že na tejto úrovni významnosti nie je splnená nulová hypotéza.

Záver objasňuje nasledujúci graf:

Graf ukazuje, ako v závislosti od úrovne významnosti vyžadovanej rovnakej hypotézy je možné akceptovať alebo odmietnuť s rovnakými údajmi. Zdroj: f. Zapata.