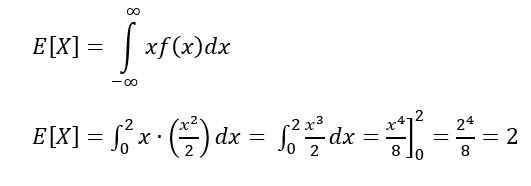Nepretržitá náhodná premenná

Vysvetlíme, aká je nepretržitá náhodná premenná, jej charakteristiky, príklady a vyriešené cvičenie

Čo je nepretržitá náhodná premenná?

A Nepretržitá náhodná premenná Je to numerická hodnota získaná náhodne, ktorá vyplýva z vykonávania experimentu a môže mať nekonečné hodnoty. To znamená, že známe dve po sebe idúce hodnoty premennej, vždy je možné nájsť medzi nimi ďalšiu strednú hodnotu.

Zhromažďovaním kontinuálnych premenných hodnôt nie je účtovníctvo a takmer vždy patrí do súboru skutočných čísel, zber kontinuálnych premenných a takmer vždy patrí do súboru reálnych čísel.

Príkladmi tohto typu premenných je postava, hmotnosť a telesná teplota osoby, ale je možné definovať nespočet z nich, niekoľko príkladov sa nachádza nižšie. Na rozdiel od nepretržitej náhodnej premennej existuje diskrétna náhodná premenná, ktorá je účtovníctvo, napríklad počet dcér v rodine alebo koľko automobilov predáva agentúra po jednom mesiaci.

Diskrétne náhodné premenné často sledujú normálne rozdelenie pravdepodobnosti. Zdroj: f. Zapata.

Kontinuálna náhodná premenná sa označuje pomocou kapitálového písmena, ako je X, a nekonečné hodnoty, ktoré premenná má, sú možnými výsledkami náhodného experimentu:

X = x₁, X₂, X₃,… ∞

Každá hodnota má určitú pravdepodobnosť výskytu a pre model, podľa ktorého sa táto pravdepodobnosť vypočítava, sa nazýva rozdelenia pravdepodobnosti.

Ale keďže X má nekonečné hodnoty, nie je možné vypočítať pravdepodobnosť špecifických hodnôt premennej. Preto je potrebné definovať funkciu f (x), nazývanú akumulovaná distribučná funkcia, alebo jednoducho distribučná funkcia, podľa ktorej sa akumulovaná pravdepodobnosť vypočítava na určitú hodnotu alebo medzi dvoma hodnotami:

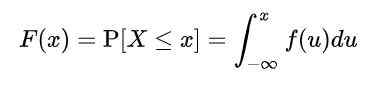
Kde f (u) získať názov funkcia hustoty. Definované týmto spôsobom, F (x) predstavuje pravdepodobnosť, že X je medzi -∞ a X.

Charakteristiky nepretržitej náhodnej premennej

Kontinuálne náhodné premenné sú úplné f (x).

Funkcia hustoty f (x) Musí splniť tieto vlastnosti:

• Funkcia f (x) Je to pozitívne: f (x)> = 0
• Oblasť pod krivkou y = f (x) Vždy sa rovná 1, to znamená, že pravdepodobnosť výskytu určitého výsledku X V intervale (-∞, +∞) je 100%.
• Pravdepodobnosť, že X je v intervale [a, b], sa vypočíta podľa nasledujúceho definovaného integrálu:

Môže vám slúžiť: Curtóza: Definícia, typy, vzorce, na čo je napríklad

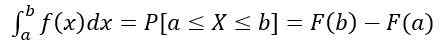
Čo je rovnocenné s oblasťou pod krivkou y = f (x), pochopený medzi do a b. Okrem::

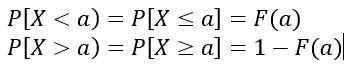
Hodnoty f (x) Nepredstavujú pravdepodobnosť, tak P [x = c] = 0. Relevantné hodnoty sú hodnoty zodpovedajúce oblasti pod krivkou y = f (x), ktoré predstavujú pravdepodobnosť.

• Odvodením distribučnej funkcie F (x) s ohľadom na X, je získané f (x).

Graf f (x) Pre nepretržitú náhodnú premennú je analogická frekvenčnému mnohouholníku, ktorý je vytvorený pre diskrétnu štatistickú premennú, s rozdielom, ktorý pre náhodnú premennú sa šírka intervalu stáva nekonečnou.

Nádej

Nádej je jedným z charakteristických mier kontinuálnej premennej. Nádej alebo očakávaná hodnota X Označuje hodnotu, ktorá sa očakáva častejšie, a je vypočítaná prostredníctvom nasledujúceho integrálu:

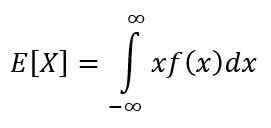
Jeho vlastnosti sú:

• E [a∙ x] = a∙ E [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ E [x] + b∙ e [y]

Kde sumy do a b Sú to skutočné čísla.

Príklady

Ako už bolo uvedené, existuje veľa situácií, v ktorých je možné definovať jednu alebo viac kontinuálnych náhodných premenných. Vo vede a ďalších oblastiach je najbežnejším časom, dĺžkou, hmotnosťou, objemom a teplotou:

Čas

S cieľom optimalizovať procesy a služby sú navrhnuté experimenty, ktoré študujú čas, ktorý sa majú vykonať,:

X = čas, ktorý vezme klienta do bankového okna.

Y = Čo zaberá miesto rýchleho občerstvenia pri podávaní objednávky.

Z = čas, v ktorom dochádza k určitej chemickej reakcii.

Výpisy

V mnohých štúdiách o ľuďoch a zvieratách sú relevantné výpisy a váhy:

X = výška dievčat v 6. kurze. Titul v každej škole v meste.

Môže vám slúžiť: Zhoda: zhodné čísla, kritériá, príklady, cvičenia

Y = váha detí pri narodení vo verejnej nemocnici.

Z = hmotnosť krav na farme.

Teplota

Teplota je relevantným parametrom v mnohých chemických procesoch, ktoré zvyčajne berú nekonečné hodnoty v určitom rozsahu:

X = teplota, pri ktorej dochádza k určitej chemickej reakcii, s vedomím, že k tomu dochádza medzi 80 ° C a 120 ° C.

Vyriešené cvičenia

Cvičenie 1

Zistite, aké sú kontinuálne náhodné premenné:

1. Počet študentov, ktorí navštevujú kávu univerzity.
2. Krvný tlak pacientov, ktorí prichádzajú na pohotovosť.
3. Dĺžka krídla vtákov, ohrozeného druhu, ktoré obývajú rezervu.
4. Čas medzi jednou osobou sa zaobchádza v banke.
5. Množstvo chybných výrobkov mesačne v továrni.
6. Hladiny cholesterolu v kurčatách farmy.
7. Množstvo pouličných žiaroviek na ulici, celkom 12.

Riešenie

1.- Počet študentov, ktorí sa zúčastnili na dni, je znecitlivený, preto táto premenná nie je nepretržitá, ale diskrétna.

2.- Je to nepretržité. Krvný tlak pacientov môže mať akúkoľvek hodnotu v danom rozmedzí.

3.- Nepretržitá premenná, pretože dĺžka krídla vtáka má akúkoľvek hodnotu medzi minimom a maximom, v závislosti od druhu.

4.- Čas medzi zákazníckym servisom je variabilný a môže mať akúkoľvek hodnotu v danom rozsahu, napríklad medzi 1 a 5 minútami.

5.- Pretože počet chybných výrobkov je účtovníctvo, ide o diskrétnu náhodnú premennú.

6.- Táto premenná je kontinuálna, pretože hladina cholesterolu v kurčatách má akúkoľvek hodnotu v predtým určenom rozsahu.

Môže vám slúžiť: doplnkové uhly: ktoré a ako sa vypočítajú, príklady, cvičenia

7.- Diskrétny. Počet svetiel osvetlenia, ktoré pracuje, je účtovná suma.

Cvičenie 2

Je definovaná kontinuálna náhodná premenná X = "hladina cholesterolu “ V určitej škále kurčiat farmy, ktorá má nasledujúcu funkciu hustoty f (x):

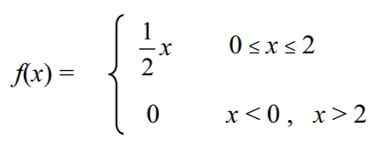
Vypočítajte nasledujúce:

1. F (x)
2. P [x ≤2]
3. Nádej Ex]

Roztok

Podľa definície uvedenej na začiatku:

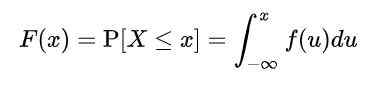
Preto, F (x) Je to funkcia v častiach. Pre interval X<0, F (x) Je to rovnaké ako 0, pre vlastnosti uvedené na začiatku.

V intervale 0≤X≤2, Neurčitý integrál je vyriešený:

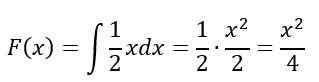
Nakoniec pre interval X> 2, F (x) = 1, Preto podľa vlastností, F (x) Zostáva to takto:

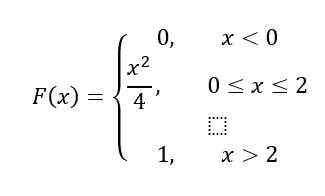
Riešenie B

Hľadaná pravdepodobnosť je F (1.2) a como x = 1.2 Nachádza sa medzi 0≤X≤2, tá časť F (x) Vyhodnotiť:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Riešenie c

Na výpočet nádeje alebo očakávanej hodnoty sa používa: