Odhad podľa intervalov
- 1872
- 439
- Blažej Hrmo
Aký je odhad intervalov?
Ten Odhad podľa intervalov Je to spôsob, ako určiť rozsah hodnôt, do ktorého je možné zahrnúť priemer populácie, na základe informácií o vzorke konečnej veľkosti, náhodne extrahovanej z celkovej populácie.
On Interval odhadu Je nižšia, pretože vzorka je väčšia, ale je širšia, ak úroveň alebo percento spoľahlivosti rovnakých zvyšuje.
Ak by ste chceli poznať priemer populácie určitej premennej v presnej podobe, potom by sa mala zvážiť celková populácia, niečo, čo nie je vždy uskutočniteľné, pretože ak je to veľmi veľká populácia, je drahé získať údaje z celá populácia. Z tohto dôvodu sa používa jedna alebo viac náhodných vzoriek celkovej populácie.
Je založená na hypotéze, že extrahovaním náhodnej vzorky, ktorá nie je zaujatá a úmerne zohľadnená všetky vrstvy, musí byť priemerná hodnota vzorky veľmi blízko k priemeru populácie priemeru populácie.
Logika naznačuje, že čím väčšie údaje o vzorke, rozdiel medzi priemernou hodnotou vzorky a priemernou hodnotou populácie je nižší.
Interval odhadu
V praxi, pokiaľ nie je známa úplná populácia, je možné nájsť iba s určitou pravdepodobnosťou interval, v ktorom je možné nájsť priemer populácie, na základe vzorky konečnej veľkosti.
V prípade populácie, ktorá sleduje normálne rozdelenie, s Štandardná odchýlka σ , ten Štandardný rozdiel Medzi priemerom populácie μ a priemerná vzorka veľkosti n je daný:
| μ - | ≤ σ / √n
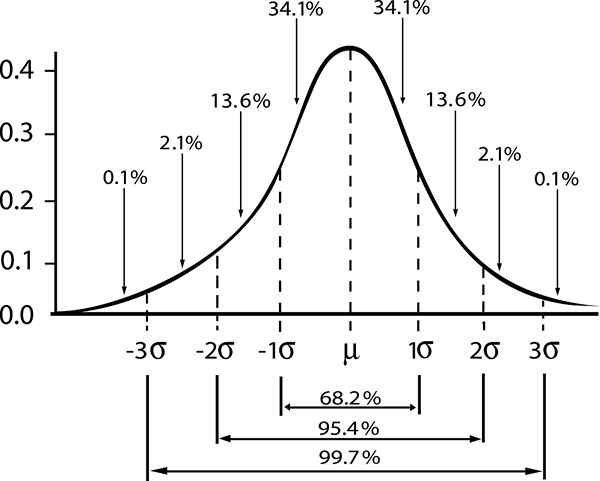
Tu slovo „štandard“ naznačuje, že 68% vzoriek veľkosti n, Majú priemernú hodnotu medzi intervalom [μ - σ / √n, μ + σ / √n].
Môže vám slúžiť: Kritériá deliteľnosti: Čo sú to, aké sú použitie a pravidláŠtandardný odhad
Alternatívnou interpretáciou vyššie uvedeného by bolo povedať, že priemerná populácia získaná zo vzorky veľkosti n a priemerná hodnota sa chápe v intervale [ - σ / √n, + σ / √n], S pravdepodobnosťou 68%.
Vo väčšine skutočných prípadov nie je možné poznať štandardnú odchýlku populácie, takže σ Je aproximovaný štandardnou odchýlkou vzorky siež, čo sa vypočíta takto:
S = √ (∑ (xJo - )2 / √ (n-1).
Odtiaľ dostanete interval, ktorý by mohol obsahovať priemer populácie s 68% úrovňou spoľahlivosti (štandardná úroveň spoľahlivosti), daná:
-s / √n ≤ μ ≤ + s / √n
Tento interval merania populácie je známy ako štandardný interval odhadu a bol získaný iba s údajmi dostupnými vo veľkosti n.
Z predchádzajúceho vzorca vyplýva, že ak ste chceli posilniť interval odhadu na polovicu, je to potrebné štvornásobok Veľkosť vzorky.
Odhad podľa intervalov spoľahlivosti
V niektorých štúdiách môže byť štandardná úroveň 68% dostatočná, potom je potrebné určiť intervaly s ľubovoľnou úrovňou spoľahlivosti γ.
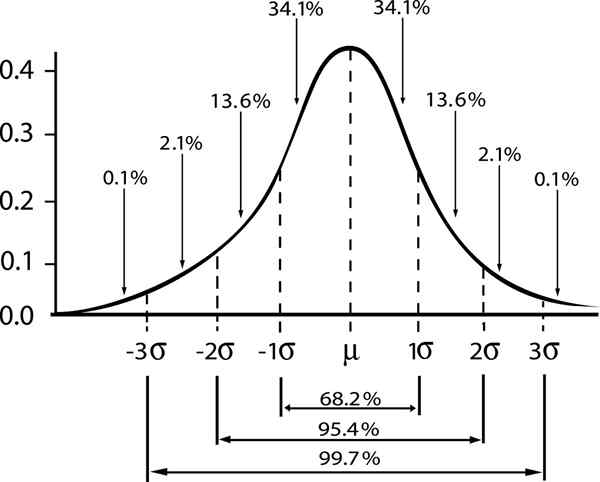Je zobrazený vzťah medzi maržou spoľahlivosti a intervalom v gaussovskom rozložení Ak označíme ε Štandardná chyba s/√n, Potom chyba odhadu pre úroveň spoľahlivosti γ bude daný:
E = zy⋅ε.
Kde Zy Je to číslo, ktorým sa vynásobí štandardná chyba, a tak získajte maržu chyby s ľubovoľnou úrovňou spoľahlivosti γ.
Získať faktor Zy, postupovať takto:
Môže vám slúžiť: Racionálne čísla: Vlastnosti, príklady a operácieKrok 1
Je hovor úroveň významnosti α zodpovedá úrovni dôvery γ podľa nasledujúceho vzorca:
α = 1 - γ
Krok 2
Hodnota je určená:
Krok 3
Vyčistí sa Zy Rovnica:
N (z y) = 1 - a/2
Pretože ide o integrálnu rovnicu, táto vôľa sa získa z normálnych distribučných tabuliek pomocou metódy lineárnej interpolácie.
Krok 4
Alternatívne k použitiu tabuliek štatistické funkcie začlenené do tabuliek, ako napríklad Vynikať, ani Hárok. Tieto programy obsahujú normálnu inverznú funkciu N-1, takže korekčný faktor Zy Získava sa priamo hodnotenie tejto inverznej funkcie:
Zy = n-1(1 - a/2).
Typické intervaly dôvery
Najčastejšie používané úrovne spoľahlivosti sú:
- Zy = 1; štandardná úroveň dôvery γ = 0,68.
- Zy = 2; úroveň sebavedomia γ = 0,95 (alebo úroveň významnosti 5%).
- Zy = 3; úroveň sebavedomia γ = 0,997 (alebo 0,3%hladina významnosti)
Príklady
Príklad 1
Určite priemerný hmotnostný interval novorodencov počas augusta v auguste vo veľkom meste na základe náhodnej vzorky 100 detí, v ktorej bola získaná priemerná hmotnosť 3100 gramov so štandardnou odchýlkou vzorky S = 1500 gramov.
Riešenie
Po prvé, určuje sa štandardná chyba vzorky:
ε = s/√n = (1500 g)/√100 = 150 g.
Preto, od tejto vzorky, je možné vyvodiť, že priemerná hmotnosť detí narodených v auguste v tomto meste je medzi 2950 g a 3250 g, s pravdepodobnosťou 68%.
Príklad 2
Predpokladajme, že veľkosť vzorky detí narodených v tom istom mesiaci augusta a v tom istom meste príkladu 1. Priemerná hmotnosť vzorky je 3100 g so štandardnou 1500 g disperziou.
Môže vám slúžiť: rozklad prírodných čísel (príklady a cvičenia)Z tejto novej vzorky sa vyžaduje odhad priemerného hmotnostného intervalu novorodencov tohto mesta.
Riešenie
Teraz sa štandardná chyba znižuje v faktore 1/√2, Takže nová štandardná chyba priemernej hmotnosti bude 106 g.
Potom z tejto novej vzorky možno odhadnúť, že priemerná hmotnosť novorodencov je v rozmedzí 2994 g až 3206 g, s pravdepodobnosťou 68%.
Cvičenia
Cvičenie 1
Určite priemerný rozsah hmotnosti novorodencov v auguste, počnúc od vzorky uvedenej v príklade 1, s pravdepodobnosťou 95%.
Riešenie
Úroveň spoľahlivosti 95% zdvojnásobuje priemerný rozsah hmotnosti v porovnaní s úrovňou spoľahlivosti 68%.
Priemerná hmotnosť novorodencov je preto zahrnutá v rozmedzí 2800 gramov pri 3400 gramoch s 95% istotou.
Cvičenie 2
Odhad s 99,7% úrovňou spoľahlivosti Interval, v ktorom sa zistí priemerná hmotnosť novorodencov z veľkého mesta, ak je k dispozícii vzorka s priemernou hmotnosťou 100 detí rovnajúcich sa 3100 g a so štandardnou odchýlkou vzorky S = 1500 g.
Riešenie
Priemerná marža chybovosti s hmotnosťou s 99,7% istoty bude trojnásobná priemerná chyba, to znamená:
3*1500/√ 100.
Potom sa z tejto vzorky odvodzuje, že priemerná hmotnosť novorodencov bude zahrnutá do intervalu: 2650 gramov na 3550 gramov, s úrovňou istoty 99,7%.
Z tohto výsledku sa pozoruje, že pri väčšej úrovni istoty zvyšuje neistotu priemernej hmotnosti do oveľa širšieho intervalu.