Relatívnych bratrancov Čo sú, vysvetlenie, príklady

Sa volá relatívny bratranci (Coprmimos alebo bratranci vo vzťahu k sebe) s akýmikoľvek pármi celých čísel, ktoré nemajú spoločný deliteľ, s výnimkou 1. Inými slovami, dve celé čísla sú relatívnymi bratrancami, ak sú v ich zlyhaní v hlavných číslach, nemajú spoločný faktor.

Napríklad, ak sú vybrané 4 a 25, rozklady v hlavných faktoroch každého z nich sú 2² a 5². Ako je zrejmé, nemajú žiadny spoločný faktor, preto sú 4 a 25 relatívnych bratrancov.

Na druhej strane, ak si vyberiete 6 a 24, pri rozkladaní hlavných faktorov sa získa, že 6 = 2*3 a 24 = 2³*3.

Ako je vidieť, tieto posledné dva výrazy majú aspoň jeden spoločný faktor, preto nie sú relatívnymi bratrancami.

Charakteristiky relatívnych bratrancov

Detail, s ktorým musí starostlivosť.

Na druhej strane, definícia vyššie je možné zhrnúť takto: dve celé čísla „A“ a „B“ sú relatívnymi bratrancami, ak je ich maximálny spoločný deliteľ 1, to znamená MCD (A, B ) = 1.

Dva okamžité závery tejto definície sú také:

-Ak je „a“ (alebo „b“) hlavným číslom, potom MCD (a, b) = 1.

-Ak sú „a“ a „b“ prvotné čísla, potom MCD (a, b) = 1.

To znamená, že ak je aspoň jedno z vybraných čísel hlavným číslom, potom pár čísel sú relatívnymi bratrancami.

Ďalšie funkcie

Ďalšie výsledky používané na určenie, či sú dve čísla relatívnych bratrancov, sú:

-Ak sú dve celé čísla po sebe idúce, potom sú to relatívne bratrance.

-Dve prírodné čísla „A“ a „B“ sú relatívnymi bratrancami, ak a iba vtedy, ak čísla “(2^a) -1" a "(2^b) -1" sú relatívne bratrance.

-Dve celé čísla „A“ a „B“ sú relatívnymi bratrancami, ak a iba vtedy, ak pri grafickom bode (a, b) v karteziánskej rovine a zostavte čiaru, ktorá prechádza cez pôvod (0,0) a (a , b), toto neobsahuje žiadny bod s celkovými súradnicami.

Príklady

1.- Zvážte celé čísla 5 a 12. Rozklad v hlavných faktoroch oboch čísel je: 5 a 2²*3. Záverom možno povedať, že MCD (5,12) = 1, preto 5 a 12 sú relatívnych bratrancov.

2.- Nechajte čísla -4 a 6. Potom -4 = -2² a 6 = 2*3, takže MCD (-4,6) = 2 ≠ 1. Záverom -4 a 6 nie sú relatívnymi bratrancami.

Ak čiara, ktorá prechádza usporiadanými pármi (-4,6) a (0,0), a na určenie rovnice uvedenej čiary je možné overiť, že to prechádza bodom (-2,3).

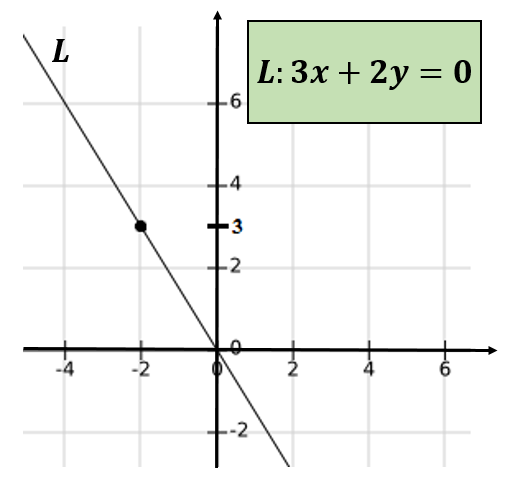
Opäť sa dospelo k záveru, že -4 a 6 nie sú relatívnymi bratrancami.

3.- Čísla 7 a 44 sú relatívnymi bratrancami a môžu byť ukončené rýchlo vďaka tomu, čo už bolo povedané, pretože 7 je hlavné číslo.

4.- Zvážte čísla 345 a 346. Keďže sú dve po sebe idúce čísla, overí sa, že MCD (345 346) = 1, preto 345 a 346 sú relatívnych bratrancov.

5.- Ak sa zvažujú čísla 147 a 74, potom sú to relatívne bratrance, pretože 147 = 3*7² a 74 = 2*37, preto MCD (147,74) = 1.

6.- Čísla 4 a 9 sú relatívnych bratrancov. Aby ste to demonštrovali, môžete použiť druhú charakterizáciu uvedenú vyššie. Naozaj, 2^4 -1 = 16-1 = 15 a 2^9-1 = 512-1 = 511.

Získané čísla sú 15 a 511. Rozklad v hlavných faktoroch týchto čísel je 3*5 a 7*73, takže MCD (15 511) = 1.

Ako vidíte, používanie druhej charakterizácie je dlhšia a namáhavejšia práca na jej priame overenie.

7.- Zvážte čísla -22 a -27. Potom je možné tieto čísla prepísať takto: -22 = -2*11 a -27 = -33. Preto sú MCD (-22, -27) = 1, takže -22 a -27 sú relatívne bratrance.