Vysvetlenie manometrického tlaku, vzorce, rovnice, príklady

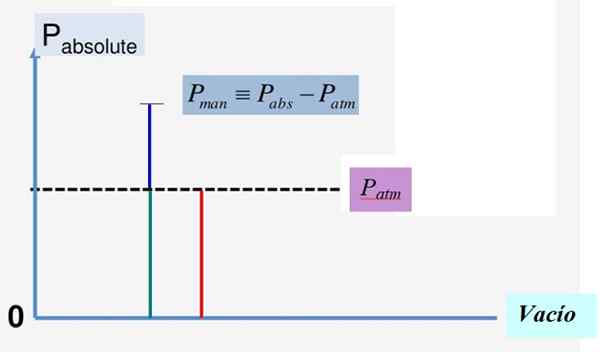
Ten tlak P_m Je to ten, ktorý sa meria vo vzťahu k referenčnému tlaku, ktorý je vo väčšine prípadov vybraný ako atmosférický tlak P_Bankomat na hladine mora. Je to potom a Relatívny tlak, ďalší termín, pre ktorý je tiež známy.

Ďalším spôsobom, ako sa tlak zvyčajne meria, je porovnávanie s absolútnou prázdnotou, ktorej tlak je vždy nulová. V tomto prípade sa hovorí o absolútny tlak, za čo označíme, ako P_do.

postava 1. Absolútny tlak a manometrický tlak. Zdroj: f. Zapata.

Matematický vzťah medzi týmito tromi množstvami je:

P_do = P_Bankomat + P_m

Preto:

P_m = P_do - P_Bankomat

Obrázok 1 tento vzťah pohodlne ilustruje. Pretože vákuový tlak je 0, absolútny tlak je vždy pozitívny a to isté platí pre atmosférický tlak p_Bankomat.

Manometrický tlak sa zvyčajne používa na označenie tlakov nad atmosférickým tlakom, ako je tlak prenášaný pneumatikami alebo tlak na spodnej časti mora alebo bazéna, ktorý je vyvíjaný hmotnosťou vodného stĺpca. V týchto prípadoch P_m > 0, od P_do > P_Bankomat.

Avšak sú absolútne tlaky pod P_Bankomat. V týchto prípadoch P_m < 0 y recibe el nombre de vákuový tlak A nemalo by sa zamieňať s tlakom už opísaného tlaku vákua, čo je neprítomnosť častíc schopných vyvíjať tlak.

[TOC]

Vzorce a rovnice

Tlak v tekutine -kvapalina alebo plyn -je jednou z najvýznamnejších premenných vo svojej štúdii. V stacionárnej tekutine je tlak rovnaký vo všetkých bodoch v rovnakej hĺbke bez ohľadu na orientáciu, zatiaľ čo pohyb tekutín v potrubiach je spôsobený zmenami tlaku.

Priemerný tlak je definovaný ako kvocient medzi silou kolmou na povrch F_⊥ a oblasť uvedeného povrchu A, ktorá je matematicky vyjadrená nasledovne:

P = f_⊥ /

Tlak je skalárne množstvo, ktorého rozmery sú sily na jednotku plochy. Jednotky vášho opatrenia v medzinárodnom systéme jednotiek (SI) sú Newton/M², nazývaný Pascal a skrátený ako PA, na počesť Blaise Pascal (1623-1662).

Násobky ako kilogram (10³) a mega (10⁶) Často sa používajú, pretože atmosférický tlak je zvyčajne v rozmedzí 90.000 - 102.000 PA, čo sa rovná: 90 - 102 kPa. Tlaky rádov mega pascalov nie sú zriedkavé, takže je dôležité oboznámiť sa s predponami.

V anglo -saxonových jednotkách sa tlak meria v librách/nohe², Bežná vec sa však musí robiť v librách/palec² ani psi (Libry-force na štvorcový palec).

Môže vám slúžiť: Prenos tepla: zákony, prenosové formuláre, príklady

Variácia tlaku s hĺbkou

Čím viac sa ponoríme do vody z bazéna alebo do mora, tým väčší tlak prežívame. Naopak, zvyšujúca sa výška, atmosférický tlak klesá.

Priemerný atmosférický tlak na hladine mora je stanovený v 101300 PA alebo 101.3 kpa, zatiaľ čo v jamke Mariana v západnom Pacifiku - najväčšia hĺbka, ktorá je známa - je asi 1000 -krát vyššia a na vrchole Everest je iba 34 kPa.

Je zrejmé, že tlak a hĺbka (alebo výška) súvisia. Aby som to vedel v prípade pokojovej tekutiny (statická rovnováha), považuje sa za tekutú časť s tekutinou na tvare disku, obmedzenú v nádobe (pozri obrázok 2). Disk má prierez Do, váha Dw a výška D Y.

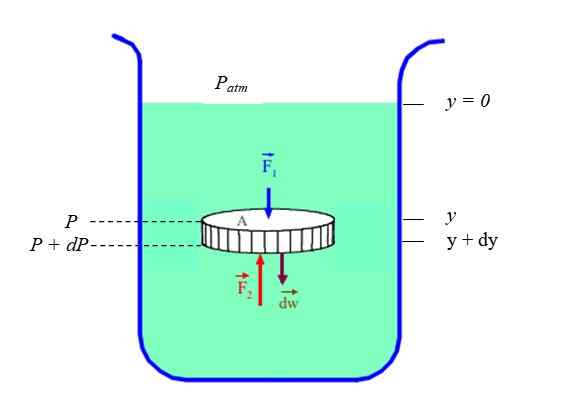Obrázok 2. Diferenciálny prvok statickej rovnovážnej tekutiny. Zdroj: Fanny Zapata.

Zavoláme P pri tlaku, ktorý existuje do hĺbky “a„A P + DP pri tlaku, ktorý existuje do hĺbky (a + dy). Pretože hustota ρ tekutiny je dôvodom medzi jej hmotnosťou Dm a jeho objem DV, Musíš:

ρ = dm/ dv ⇒ dm = ρ.DV

Preto váha Dw prvku je:

dw = g. Dm = ρ.g.DV

A teraz platí Newtonov druhý zákon:

Σ f_a = F₂ - F₁ - Dw = 0

(P + dp).A - P.Do - ρ.g.Dv = 0

(P + dp).A - P.Do - ρ.g. Do. Dy = 0

Dp = ρ.g.D Y

Roztok diferenciálnej rovnice 

Integrácia oboch strán a zvažovanie tejto hustoty ρ, ako aj gravitácia g Sú konštantné, existuje vyhľadaný výraz:

P₂ - P₁ = ΔP = ρ.g.(a₂ - a₁)

Δp = ρ.g. Δa

Ak je v predchádzajúcom výraze vybraný P₁ ako je atmosférický tlak a a₁ Ako povrch kvapaliny a₂ Nachádza sa v hĺbke h a Δp = P₂ - P_Bankomat Je to manometrický tlak v závislosti od hĺbky:

P_m = ρ.g.h

Ak potrebujete absolútnu hodnotu tlaku, atmosférický tlak sa jednoducho pridá k predchádzajúcemu výsledku.

Príklady

Pre manometrické tlakové meranie sa používa zariadenie tlakomer, ktoré vo všeobecnosti ponúkajú tlakové rozdiely. Nakoniec bude opísaný princíp činnosti manometru tlaku u -, ale teraz pozrime niekoľko dôležitých príkladov a dôsledkov predtým odpočítanej rovnice.

Pascalový princíp

Rovnica ΔP = ρ.g.(a₂ - a₁) Môže byť napísaný ako  P = PO + ρ.g.h, kde P je tlak v hĺbke h, zatiaľ čo P_ani Je to tlak na povrch tekutiny, zvyčajne P_Bankomat.

Je zrejmé, že zakaždým, keď sa zvýšite Po, zvýšenie P v rovnakom množstve, pokiaľ ide o tekutinu, ktorej hustota je konštantná. To je presne to, čo malo zvážiť ρ konštantné a umiestnite ho mimo integrál vyriešené v predchádzajúcej časti.

Môže vám slúžiť: jednoduchý harmonický pohyb

Princíp Pascal uvádza, že akékoľvek zvýšenie tlaku tekutiny obmedzenej v rovnováhe sa prenáša bez akýchkoľvek variácií do všetkých bodov uvedenej tekutiny. Prostredníctvom tejto vlastnosti je možné vynásobiť silu F₁ aplikované na malú ľavú ľavú zľava a získajte F₂ napravo.

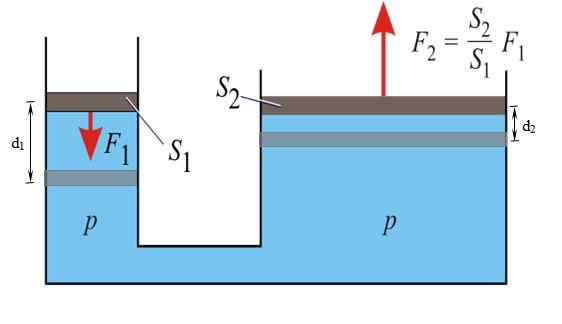Obrázok 3. V hydraulickom tlači sa uplatňuje princíp Pascal. Zdroj: Wikimedia Commons.

Automobilové brzdy pracujú pod týmto princípom: Na pedál sa aplikuje relatívne malá sila, ktorá sa stáva hlavnou silou na brzdovom valci na každom kolese, a to vďaka tekutine použitej v systéme.

Stevinov hydrostatický paradox

Hydrostatický paradox uvádza, že sila v dôsledku tlaku tekutiny na spodnej časti nádoby môže byť rovnaká, väčšia alebo menšia ako hmotnosť samotnej tekutiny. Ale pri vkladaní nádoby na stupnicu bude normálne zaznamenávať hmotnosť tekutiny (plus jeden z nádoby samozrejme). Ako vysvetliť tento paradox?

Začneme od skutočnosti, že tlak na spodnej časti kontajnera závisí výlučne od hĺbky a je nezávislý od formulára, ako je odvodené v predchádzajúcej časti.

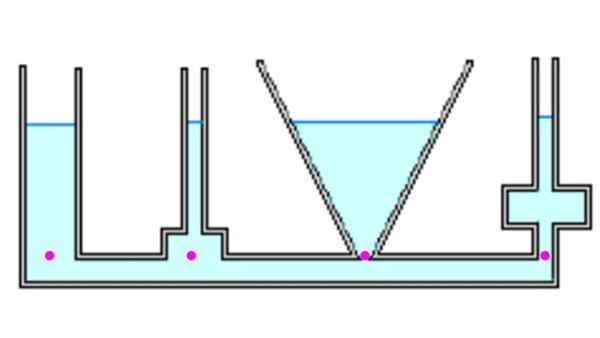Obrázok 4. Kvapalina dosahuje rovnakú výšku vo všetkých nádobách a tlak na pozadí je rovnaký. Zdroj: f. Zapata.

Pozrime sa na niektoré rôzne nádoby. Pri komunikácii, keď sú naplnené tekutinou, každý dosiahne rovnakú výšku h. Významné body majú rovnaký tlak, pretože sú v rovnakej hĺbke. Sila spôsobená tlakom v každom bode sa však môže líšiť od hmotnosti (pozri príklad 1 nižšie).

Cvičenia

Cvičenie 1

Porovnajte silu vyvíjanú tlakom na spodnej časti každej z nádob s hmotnosťou tekutiny a vysvetlite, prečo z rozdielov, ak existujú.

Kontajner 1 

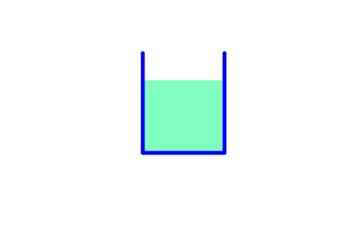Obrázok 5. Tlak v pozadí je rovnaký v rozsahu hmotnosti tekutiny. Zdroj: Fanny Zapata.

V tejto kontajneri je základná plocha A: preto:

Hmotnosť tekutiny: mg = ρ.Vložka.G = ρ . Do .h . g

Tlak na dne: ρ. g. h

Sila v dôsledku tlaku: f = P.A = ρ. g. h. Do

Hmotnosť a sila v dôsledku tlaku sú rovnaké.

Kontajner 2 

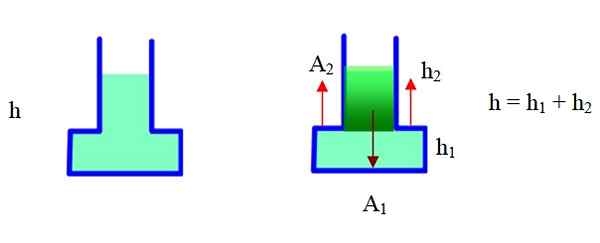Obrázok 6. Sila spôsobená tlakom v tejto nádobe je väčšia ako hmotnosť. Zdroj: f. Zapata.

Kontajner má úzku časť a širokú časť. V správnej schéme bola rozdelená na dve časti a použije geometriu na nájdenie celkového objemu. Oblasť a₂ je vonkajší do nádoby, h₂ Je to výška úzkej časti, h₁ Je to výška širokej časti (základňa).

Môže vám slúžiť: Pleiades: História, pôvod a kompozícia

Kompletný objem je objem základne + objem úzkej časti. S týmito údajmi máte:

Hmotnosť tekutiny: M . G = ρ . g. V = ρ . g. [₁ .h₁+ (₁ -Do₂) .h₂] =

= ρ . g (a₁.haš₂h₂) = ρ . g . Do₁.H - ρ . g . Do._. h₂ (Použitie h = h₁ +h₂)

Tlak na dne: p = ρ. g. h

Sila na dne v dôsledku tlaku: f = P. Do₁ = ρ. g. h. Do₁

Porovnanie hmotnosti tekutiny so silou v dôsledku tlaku, ktorý je poznamenaný, že je väčší ako hmotnosť.

Čo sa stane, je to, že tekutina tiež vyvíja pevnosť na strane kroku v nádobe (pozri červené šípky obrázku), ktoré sú zahrnuté v predchádzajúcom výpočte. Táto sila proti tým, ktorí sú vyvíjaní, a hmotnosť zaznamenaná mierkou je výsledkom týchto. Podľa toho je veľkosť hmotnosti:

W = sila na pozadí - sila na rozloženej časti = ρ . g . Do₁.H - ρ . g . Do._. h₂

Cvičenie 2

Obrázok zobrazuje tlakomer s otvorenou trubicou. Skladá sa z trubice U, v ktorej je jeden z koncov pri atmosférickom tlaku a druhý sa pripája k S, systému, ktorého tlak sa bude merať.

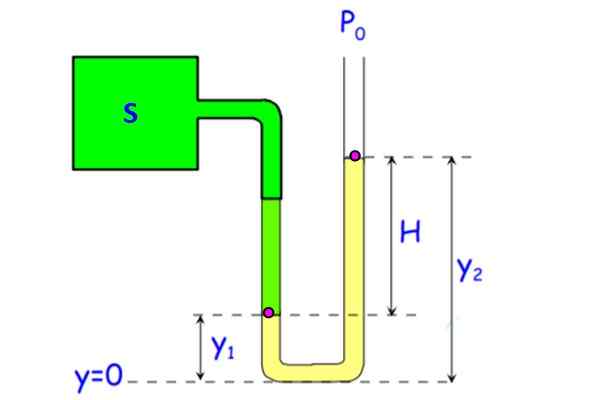Obrázok 7. Tlakomer na otvorenú trubicu. Zdroj: f. Zapata.

Kvapalina v trubici (v žltej na obrázku) môže byť voda, hoci ortuť sa používa na zníženie veľkosti zariadenia. (Rozdiel 1 atmosféry alebo 101.3 kPa vyžaduje 10 vodný stĺpec.3 metre, nič prenosné).

Žiada sa o nájdenie manometrického tlaku P_m V systéme S v závislosti od výšky H kvapalného stĺpca.

Riešenie

Tlak v pozadí pre obe vetvy trubice je rovnaký, pretože je v rovnakej hĺbke. Nechať p_Do Tlak v bode A, umiestnený v a₁ A p_B tí z bodu B, ktoré sú vo výške a₂. Pretože bod B je umiestnený v rozhraní tekutiny a vzduchu, tlak je p_ani. V tejto vetve tlakového rozchodu je tlak na dne:

PO + ρ.g.a₂

Pokiaľ ide o svoju časť, tlak na dne pre vetvu ľavej strany je:

P + ρ.g.a₁

Kde p je absolútny tlak systému a ρ je hustota tekutiny. Rovnaké oba tlaky:

PO + ρ.g.a₂ = P +ρ.g.a₁

Vyčistenie P:

P = PO + ρ.g.a₂ - ρ.g.a₁ = PO + ρ.g (a₂ - a₁) = PO + ρ.g. H

Preto manometrický tlak P_m Je to dané P - P_ani = ρ.g. H A aby mala svoju hodnotu, stačí zmerať výšku, na ktorú manometrická tekutina stúpa a vynásobí ju hodnotou g a hustota tekutín.

Odkazy

1. Cimbala, C. 2006. Mechanika tekutín, základov a aplikácií. MC. Graw Hill. 66-74.
2. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Tekutiny a termodynamika. Editoval Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Tekutina. 4. Vydanie. Pearson Vzdelanie. 53-70.
4. Shaugnessy, e. 2005. Úvod do mechaniky tekutín.Oxford University Press. 51 - 60.
5. Stylians, v. 2016. K jednoduchému vysvetleniu klasického hydrostatického paradoxu. Získané z: Haimgaifman.Súbory.Slovník.com