Vzorec hydrostatického tlaku, výpočet, príklady, cvičenia

Ten Hydrostatický tlak Je to tá, ktorá uplatňuje tekutinu v statickej rovnováhe kdekoľvek vo vnútri, buď do nej, do nej, steny nádoby alebo časť tekutiny, ktorá je súčasťou celkovej hmoty.

Spôsob, akým sa tekutiny vyvíjajú od tlaku od tuhých látok. Tieto vyvíjajú tlak, ale kvapalina alebo plyn to robia vo všetkých smeroch.

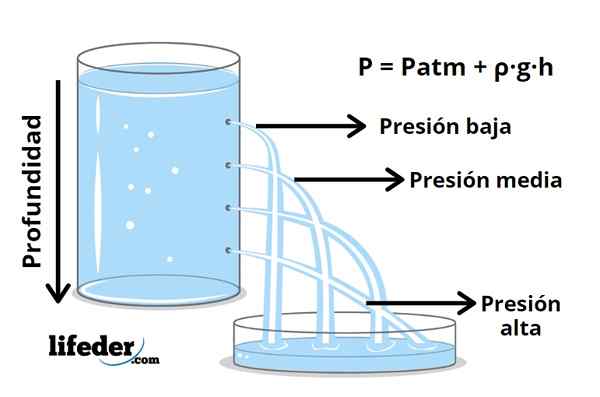
Obrázok 1- Vo väčšej hĺbke väčší tlak

Pokiaľ ide o kvapalinu, tlak sa zvyšuje s hĺbkou, ako je známe skúsenosťami, keď ponoríte do vody, v ktorej sa v ušiach pociťuje zvýšenie tlaku v ušiach. Tento tlak pochádza z hmotnosti tekutiny a nepretržitého pohybu častíc, ktoré ju tvoria, ktoré neustále zasiahli povrch tela ponorený do tekutiny.

Ak predpokladáme nestlačiteľnú kvapalinu, ktorá je pravdivá v drvivej väčšine aplikácií, - jej hustota zostáva konštantná a v takom prípade tlak lineárne závisí od hĺbky.

[TOC]

Vzorec

Hydrostatický tlak sa vypočítava nasledujúcim výrazom:

P = p_Bankomat + ρ · g · h

Kde:

-P Tlak vyvíjaný v bode

-P_Bankomat Je to tlak atmosféry na voľnom povrchu

-ρ je hustota tekutiny

-G je zrýchlenie gravitácie

-H je hĺbka, do ktorej chcete vypočítať hydrostatický tlak 

Vzorec zahŕňa účinky atmosféry, ale veľa tlaku alebo manometre kladie 0 do atmosférického tlaku, z tohto dôvodu je to, čo merajú, je diferenciálny tlak alebo relatívny tlak, tiež nazývaný tlak:

P_m = ρ · g · h

Pokiaľ ide o plyny, sú veľmi ľahko komprimované alebo rozšírené. Preto je jeho hustota, ktorá je dôvodom medzi hmotnosťou a objemom, zvyčajne funkciou iných parametrov, ako je výška a teplota, v prípade atmosférických plynov.

Môže vám slúžiť: magnetizácia: orbitálny a rotátny magnetický moment, príklady

Tlak, ktorý vyvíjajú plyny, sa zvyčajne nazýva aerostatický tlak, termín hydrostatický tlak na rezervované kvapaliny.

Príklady hydrostatického tlaku

Hydrostatický tlak závisí iba od hĺbky, takže tvar alebo plocha základne nádoby nie je relevantný.

Pretože tlak P je definovaný ako kolmú zložku sily F na jednotku oblasti A:

P = f/a

Potom sila vyvíjaná kvapalinou na spodnej časti nádoby sa môže líšiť, ale rozloženie v rôznych rozšíreniach, tlak, ktorý je pomerom sily/oblasti, je rovnaký pre body do rovnakej hĺbky.

Zvážte nádoby na obrázku. Tlak je rovnaký pre všetky červené body, ktoré sú na rovnakej úrovni, hoci v centrálnej nádobe -viac ako šírka -, z ktorých je valcovitá a tenká trubica extrémnej ľavej strany extrémnej ľavej úrovne, je väčšia tekutina.

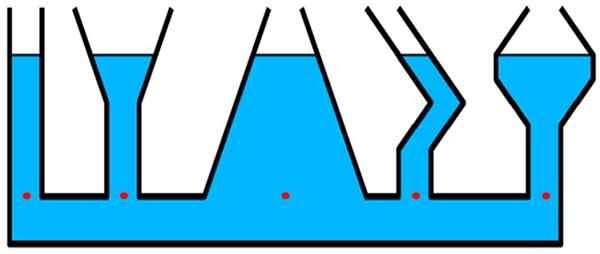Obrázok 2.- Tlak v ktoromkoľvek z červených bodov je rovnaký, bez ohľadu na tvar nádoby. Zdroj: Wikimedia Commons.

Štruktúry, kde je relevantný hydrostatický tlak

-Steny priehrady: Aj keď je sila rovnaká pre všetky body plochého dna, na zvislej stene, ktorú rastie, keď sa zvyšuje hĺbka, takže oporné steny sú v základni širšie ako v hornej časti.

-Na stenách a spodnej časti bazéna.

-V hviezdach ako naše slnko, kde hydrostatický tlak vyvažuje silu gravitácie a udržuje hviezdu v prevádzke. Keď je rovnováha porušená, hviezda sa zrúti a trpí extrémnymi zmenami v jej štruktúre.

Môže vám slúžiť: Aký je magnetický moment?

-Kvapalinové skladovacie nádrže určené na odolávanie hydrostatického tlaku. Nielen steny, ale aj brány, ktoré uľahčujú plnenie a extrakciu. Pre svoj dizajn sa berie do úvahy, ak je kvapalina korozívna a tiež tlak a sila, ktorú vyvíja podľa svojej hustoty.

-Pneumatiky a balóny, ktoré sú infikované takým spôsobom, aby odolali tlaku tekutiny (plyn alebo kvapalina) bez roztrhnutia.

-Akékoľvek ponorené telo, ktoré zažíva vertikálny ťah alebo „reliéf“ svojej hmotnosti, a to vďaka hydrostatickému tlaku vyvíjaného kvapalinou. Toto je známe ako Archimedesov princíp.

Cvičenia

Princíp Archimedes potvrdzuje, že ponorením tela úplne alebo čiastočne zažije vertikálnu silu nahor, známu ako ťah. Veľkosť ťahu sa numericky rovná hmotnosti objemu vody vytlačenú objektom.

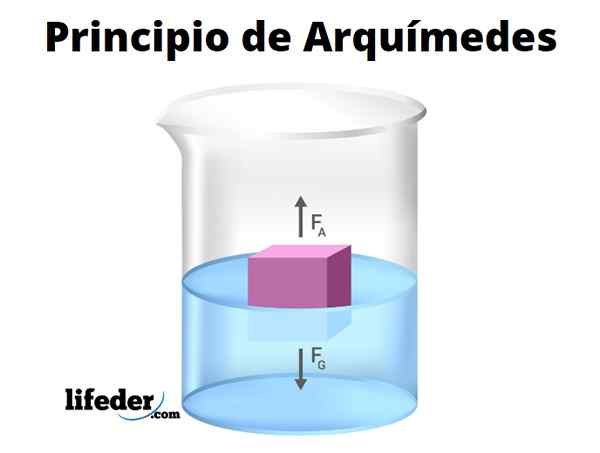
Byť ρ_plynulý Hustota tekutiny, v_siež Ponorený objem, g zrýchlenie gravitácie a B veľkosť ťahu, ktorú môžeme vypočítať podľa nasledujúceho výrazu:

B = ρ_plynulý .Vložka_siež .g

- Cvičenie 1

Obdĺžnikový blok, ktorého rozmery sú 2.0 cm x 2.0 cm x 6.0 cm pláva v sladkej vode s najdlhšou vertikálnou osou. Dĺžka bloku, ktorý vyniká nad vodou, je 2.0 cm. Vypočítať hustotu bloku.

Riešenie

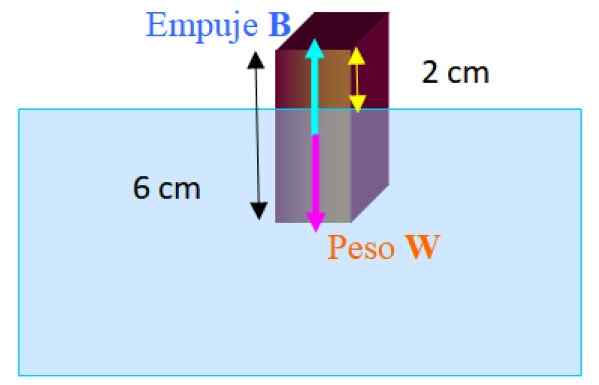Obrázok 3.- Diagram voľného tela pre blok, ktorý pláva čiastočne ponorené do vody. Zdroj: f. Zapata.

Sily pôsobiace na blok sú hmotnosť W dole a ťah B hore. Keď blok pláva v rovnováhe, máte:

∑ f_a = B - w = 0

B = w

Veľkosť hmotnosti w je produktom hmotnosti m bloku v dôsledku zrýchlenia gravitácie. Použijeme definíciu hustoty ρ_ani Rovnako ako kvocient medzi hmotnosťou m a objem Vložka bloku:

Môže vám slúžiť: Sriepustná analýza: koncepty, metódy, príklady

ρ_ani = m / v → m = ρ_ani . Vložka

Pohyb je:

B = ρ_plynulý .Vložka_siež .g

Vyrovnávanie veľkosti ťahu a rozsahu hmotnosti:

ρ_plynulý .Vložka_siež .G = ρ_ani . Vložka.g

Gravitácia je zrušená za to, že je faktorom na oboch stranách a hustota bloku sa dá vyčistiť ako:

ρ_ani = ρ_plynulý . (V_siež  / V)

Hustota vody v medzinárodných systémových jednotkách je 1000 kg/m³. Celkový objem V a ponorené v_siež, Vypočítajú sa pomocou V = šírka x vysoká x hĺbka:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

Vložka_siež = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Výmena hodnôt:

ρ_ani = ρ_plynulý . (V_siež  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Cvičenie 2

Vypočítajte ponorené objemové percento kusu ľadu vznášajúceho sa v morskej vode na 0 ° C.

Riešenie

Ľad pláva vo vode, pretože jej hustota je nižšia: 916.8 kg/m³, Čo znamená, že sa rozširuje, keď sa ochladí, na rozdiel od väčšiny látok, že keď sa zahrievajú, zvyšujú svoj objem.

Obrázok 4. Takmer celý objem ľadovca zostáva ponorený. Zdroj: Pixabay.

Je to veľmi šťastná okolnosť na celý život, odvtedy masy vody zamrznú iba na povrchu a zostáva v hĺbke kvapalina.

Hustota morskej vody je o niečo väčšia ako hustota sladkej vody: 1027 kg/m³. Vypočítame frakciu objemu v_siež  / V:

Vložka_siež  / V = ​​ρ_ani / ρ_plynulý = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

To znamená, že približne 89 % ľadu zostáva ponorených pod vodou. Na mori je viditeľné iba 11 %.

Odkazy

1. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
2. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
3. Cimbala, C. 2006. Mechanika tekutín, základov a aplikácií. MC. Graw Hill.
4. Hibbeler, R. 2015. Tekutina. 1. Edimatizovať. Pearson.
5. Mott, r.  2006. Tekutina. 4. Vydanie. Pearson Vzdelanie.
6. Streeter, v. 1999. Tekutina. McGraw Hill.