Aké sú časti frakcie? (Príklady)
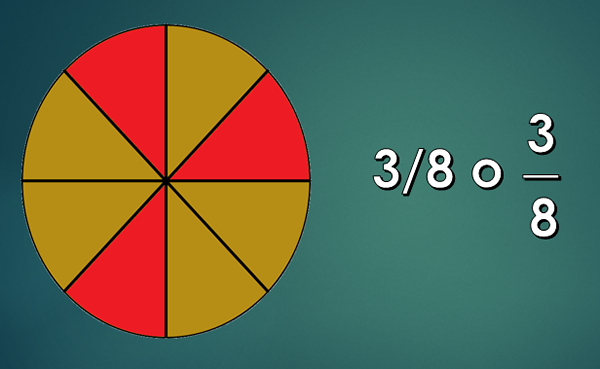
- 3189
- 401
- Tomáš Klapka
Ten časti frakcie Sú rozdelené na tri, ktoré sú: ich čitateľ, vodorovná alebo diagonálna bar a jeho menovateľ. Preto, ak chcete označiť frakciu „A Room“, notácia je 1/4, kde číslo nad lištou je čitateľ a nižšie je menovateľom menovateľ.
Keď hovoríte o frakciách, naozaj hovoríte o častiach, v ktorých je potrebné rozdeliť úplnosť niečoho. Čísla, ktoré tvoria zlomok, sú celé, to znamená, že čitateľ a menovateľ sú celé čísla s výhradou, že menovateľ musí byť vždy odlišný od nuly.
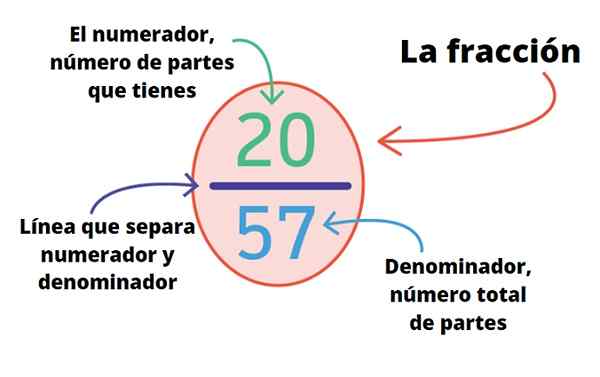
Preto sú časti frakcie:
- Čitateľ (horná časť).
- Menovateľ (dolná časť).
Definícia
Formálna matematická definícia frakcií je: sada tvorená všetkými prvkami formy P/Q, kde „P“ a „Q“ sú celé čísla s „Q“ odlišným od nuly.
Táto sada sa nazýva sada racionálnych čísel. Racionálne čísla sa tiež nazývajú zlomené čísla.
Vzhľadom na akékoľvek racionálne číslo v jeho desatinnom výraze môžete vždy získať zlomok, ktorý ho generuje.
Príklady použitia frakcií
 3 časti 8
3 časti 8 Základný spôsob, akým učia dieťaťu, koncept zlomku je distribúcia kúskov objektu alebo súboru objektov. Napríklad:
Narodeninová torta
Ak chcete rozdeliť kruhový narodeninový tortu medzi 8 deťmi tak, aby dostali všetky deti rovnaké množstvo koláča.
Môže vám slúžiť: stupne slobody: Ako ich vypočítať, typy, príkladyZačína sa rozdelením tohto koláča do 8 rovnakých častí, ako je uvedené nižšie. Potom je každé dieťa distribuované kusom koláča.
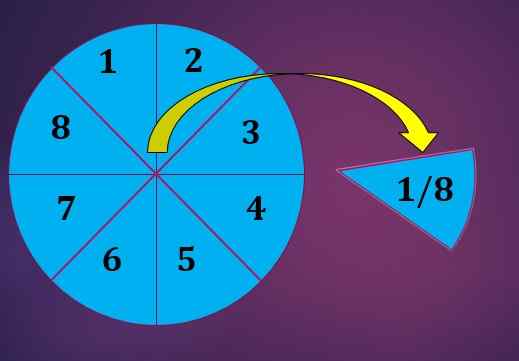
Spôsob, ako reprezentovať frakciu (časť) koláča, ktorý sa dotýkal každého dieťaťa, je 1/8, kde čitateľ je 1, pretože každé dieťa dostalo iba jeden kus koláča a menovateľ je 8, pretože koláč bol rozrezaný na 8 rovnakých diely.
Cukrovinky
Maria kúpila 5 cukroviniek pre svoje dve deti. Dal Juan 2 cukríky a Rosa dala 3 cukríky.
Celková cukrovina je 5 a musí byť distribuovaná 5. Podľa distribúcie, ktorú urobila María, sa Juan dotkol 2 cukrovinky celkom 5, takže zlomok cukroviniek, ktorú dostal, je 2/5.
Keďže Rosa dostala 3 cukríky s celkovým počtom 5 cukroviniek, zlomok Caramelos, ktorý Rosa získala, bola 3/5.

Obdĺžnikový
Roberto a José musia namaľovať obdĺžnikový plot, ktorý je rozdelený do 17 zvislých tabuliek rovnakých rozmerov, ako je znázornené na obrázku nižšie. Ak Roberto namaľoval 8 stolov, aký zlomok plotu namaľoval José?
Celkové vertikálne tabuľky rovnakej veľkosti v plote je 17. Zlomok plotu, ktorý Roberto namaľoval, sa získa pomocou počtu stolov maľovaných Robertom a menovateľom je celkový počet tabuliek, to znamená 17.
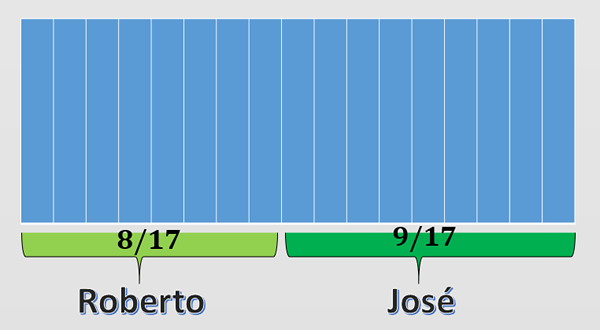
Potom zlomok plotu maľovaného Robertom bol 8/17. Na dokončenie všetkého plotu musí maľovať ďalších 9 stolov.
Týchto 9 tabuliek maľovalo José. To naznačuje, že zlomok plotu, ktorý José maľoval, bol 9/17.
Môže vám slúžiť: Činnutie riadku: vzorec a rovnice, reprezentácia, príkladyOdkazy
- Almaguer, G. (2002). Matematika 1. Redakčná limusa.
- Bussell, L. (2008). Pizza v častiach: zlomky! Gareth Stevens.
- Cofré, a., & Tapia, l. (Devätnásť deväťdesiatpäť). Ako rozvíjať matematické logické zdôvodnenie. Redakcia univerzity.
- Z mora. (1962). Matematika pre workshop. Reverzný.
- Lira, m. L. (1994). Simon a matematika: Matematický text pre druhý základný rok: kniha študentov. Andres Bello.
- Palmer, C. Jo., & Bibb, s. F. (1979). Praktická matematika: aritmetika, algebra, geometria, trigonometria a pravidlo výpočtu (Opakovanie Ed.). Reverzný.

