Až do riadkovej vzorca a rovníc, reprezentácie, príkladov

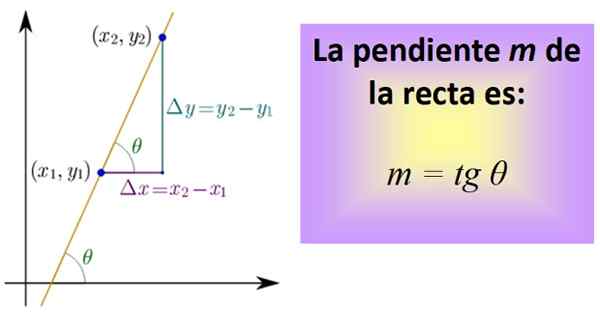
Ten prebiehajúca čiara Je to dotyčnica uhla θ, že táto čiara sa vytvára s vodorovnou osou, ktorá sa pri konvencii meria v opačnom smere ako hodinové ruky. Sklon akejkoľvek línie je vždy konštantný, a preto je jednou z jeho najdôležitejších charakteristík.

Na jeho výpočet musíte poznať dva body riadku, ktorých súradnice sú (x x₁,a₁) a (x₂,a₂). Medzi oboma bodmi je nakreslený segment, ktorý patrí do čiary a potom sú nakreslené segmenty, ktoré predstavujú vzdialenosť medzi x₁ a x₂, a medzi a₁ a a a₂, ako na spodnej postave.

postava 1. Sklon čiary je dotyčnica uhla 9. Zdroj: Wikimedia Commons.

Tri segmenty tvoria pravý trojuholník, ktorého nohy sú: δx = x₂ - X₁  a Δy = a₂ - a₁. Zodpovedajú horizontálnemu posunu a ďalšej vertikálnej.

Teraz je kvocient definovaný, nazývaný tangens uhlu 9 a skrátený TG 9, čo je presne svah m riadku:

m = tg θ = Δy / δx

Všimnite si, že pre čiaru zostáva tento uhol konštantný, bez ohľadu na body, ktoré sa majú vypočítať na jeho dotyčnicu. V každom prípade nám táto hodnota ponúka mieru toho, ako je to náklon.

Prostredníctvom súradníc vybraných bodov zostáva vzorec svahu:

M = (y - y₁ ) / (X₂ - X₁)

[TOC]

Grafická reprezentácia

Nižšie máme niekoľko situácií, v ktorých je relevantný koncept svahu. Jeho hodnotu sa dá ľahko vypočítať meraním príslušného vertikálneho a horizontálneho posunu a následným vytvorením kvocientu označeného na začiatku.

To nám dáva predstavu o svahu alebo o úpadku nejakej štruktúry, ako je rampa, strecha alebo cesta:

Môže vám slúžiť: náhodné odber vzoriek: metodika, výhody, nevýhody, príklady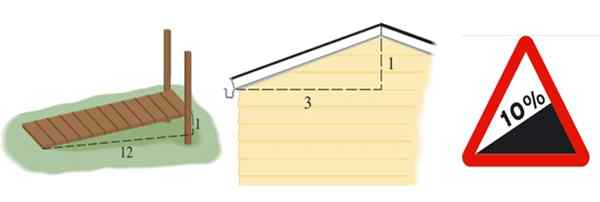 Obrázok 2. Zľava doprava svah rampy, strecha a sklon cesty, druhá sa vyjadrila v percentách. Zdroj: Stewart, J. Prececulculo a Wikimedia Commons (pravý obraz).

Sklon rampy znázornený na obrázku 2 vľavo je m = 1/12, strecha je m = 1/3 a cesta je vyjadrená v percentách. 10 % percento znamená, že za každých 100 metrov, ktoré postupujú horizontálne, zarábajú vysoké 10 metrov:

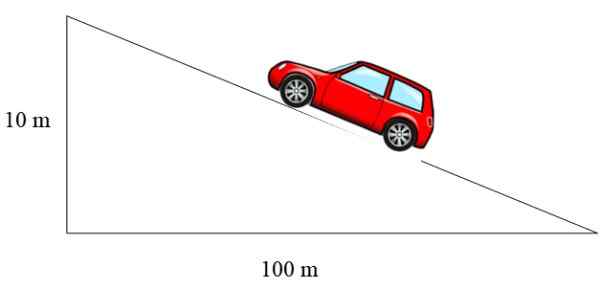Obrázok 3. Vozidlo stúpa cez svah, ktorého sklon je 10%. Zdroj: f. Zapata.

V tomto prípade je sklon 10/100 = 0.1, ktorý vyjadril ako percento, sa rovná 10%.

Typy svahov

Sklon čiary môže byť pozitívny, negatívny alebo nulová. Napríklad čiara znázornená na obrázku 1 má pozitívny sklon. Oceňujeme to okamžite, pretože vidíme, že čiara je „zdvihnutá“, ak ju vidíme zľava doprava.

Ak čiara zostúpi zľava zľava doprava, jeho sklon je negatívny. A keď je čiara vodorovná, jeho sklon je nula.

Nakoniec pre vertikálne čiary nie je sklon definovaný.

Grafické znázornenie každého typu je uvedené nižšie:

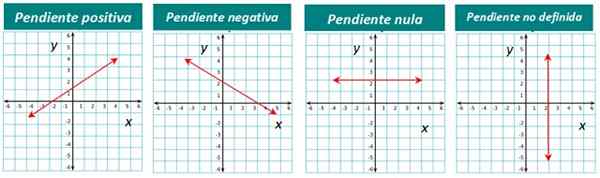Obrázok 4. Riadky podľa vášho svahu. Zdroj: f. Zapata.

Ako sa vypočíta svah?

Výpočet sklonu je veľmi jednoduchý, stačí nájsť vertikálne posunutie a horizontálne posunutie a potom medzi nimi urobiť kvocient.

Ak máte kresbu čiary v karteziánskej rovine, tieto posuny si vyberú akékoľvek dva body riadku P₁ A p₂, určenie ich súradníc a uplatňovanie definície uvedenej na začiatku:

Môže vám slúžiť: čo predstavuje dĺžku posunu šesťuholníka

M = (y - y₁ ) / (X₂ - X₁ )

Pretože hodnota svahu je nezávislá od výberu P₁ A p₂ , Budeme si vybrať bod P súradníc (x, y), ktorý patrí do línie, ktorej súradnice nie sú známe, a ďalší bod P₁ ktorých súradnice sú: (x₁,a₁).

Sklon je:

M = (y - y₁) / (x - x₁)

Môžeme vyčistiť a:

a - a₁ = m (x - x₁)

Teraz predpokladajme bod P₁ Je to priesečník čiary s vertikálnou osou, súradnice (0, b). Nahradenie v predchádzajúcej rovnici:

a - b = m (x - 0) → y = mx + b

Tento výraz je známy ako rovnica čiary vo forme Čakanie - križovatka, Pretože čiara je jednoznačne určená, keď je známa jeho sklon a priesečník s vertikálnou osou.

Vedieť iba svah nestačí na charakterizáciu čiary v lietadle, pretože nekonečné rovné by mohlo mať rovnaký svah, čo znamená, že sú paralelné, ale prechádzajú inými bodmi.

Vyriešené cvičenia

- Cvičenie 1

Nájdite sklon čiary zobrazeného na nasledujúcom obrázku:

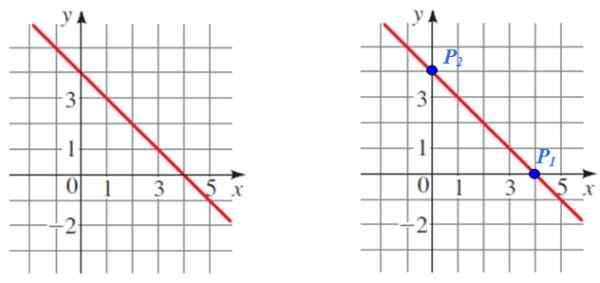Obrázok 5. Cez graf riadku sú vybrané dva body na výpočet jeho sklonu. Zdroj: f. Zapata.

Riešenie

P₁ A p₂ Sú to dva jednoduché body na čítanie, ktoré budú slúžiť na výpočet, tiež poznamenáva, že ide o príslušné križovatky s súradnicovými osami.

Súradnice každého bodu sú:

P₁ (4.0) a P₂ (0,4)

Nahradením rovnice svahu:

m = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Sklon je negatívny, čo sa očakávalo po pozorovaní grafiky.

Môže vám slúžiť: zložité čísla: vlastnosti, príklady, operácie

- Cvičenie 2

Nájdite rovnicu čiary, ktorá prechádza bodom (1, -6) a je rovnobežná s čiarou y = 2x - 3.

Riešenie

Sklon vyhľadávanej línie musí byť rovnaký ako svah y = 2x - 3, pretože sú rovnobežné. Pre túto líniu je sklon m = 2, preto ten, ktorý hľadáme, má formu:

a - a₁ = 2 (x - x₁)

Teraz nahradíme bod, ktorým prechádza náš linka: x₁ = 1 a₁ = -6.

a - (-6) = 2 (x - 1)

Preto y = 2x - 2 - 6 → y = 2x - 8

Príklady

Dve množstvá môžu súvisieť takým spôsobom, že váš graf je priamka. V takom prípade sa hovorí, že sumy majú lineárnu závislosť a sklon čiary sa dá interpretovať ako dôvod zmeny jednej premennej na druhú.

Príklad 1

Predpokladajme, že bazén je naplnený vodou do a miera konštantný. Čím viac času plynie, tým viac vody sa ukladá. Sadzba, do ktorej je fond vyplnený, je presne sklon čiary, ktorý sa týka objemu v čase:

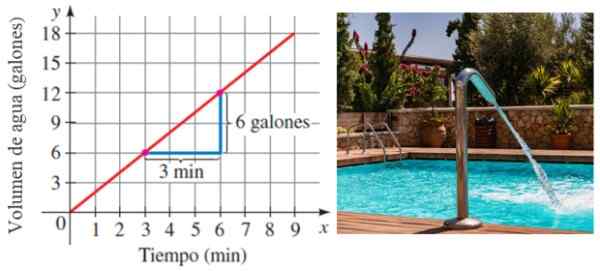Obrázok 6. Sklon ako dôvod zmeny. Zdroj: Stewart, J./Pxfuel.

V tomto príklade je bazén vyplnený rýchlosťou 6/3 galónov za minútu alebo 2 galóny/minútu.

Príklad 2

Keď sa mobilný pohyb pohybuje v priamke s konštantnou rýchlosťou, sklon polohového grafu závisí od času nie je nič iné ako uvedená rýchlosť. Graf ukazuje mobil s pozitívnou rýchlosťou, čo znamená, že sa pohybuje od pôvodu.

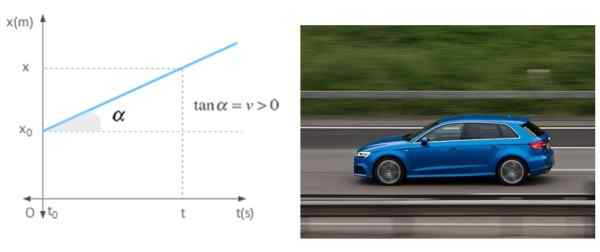Obrázok 7. Sklon grafu verzus čas je rýchlosť mobilu v rovnomernom priamom pohybe. Zdroj: Wikimedia Commons/Pixabay.

Odkazy

1. Alvarez, J. Sklon cesty. Získané z: Geogebra.je.
2. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
3. Hoffman, J. Výber matematických problémov. Zväzok 4.
4. Jiménez, r. 2008. Algebra. Sála.
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
6. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.