Rovnobežný

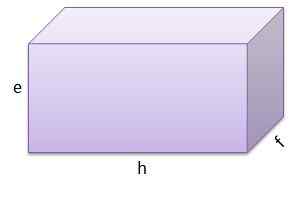
Paralepipeds sú šesťdesiaty geometrické čísla, kde sú protiklady navzájom rovnobežné. Príklad: tehla, krabica na topánky, vedro atď.

Čo je paralelnepipované?

A rovnobežný Je to geometrické telo tvorené šiestimi tvárami, ktorých hlavnou charakteristikou je, že všetky jeho tváre sú rovnobežníky a tiež jeho opačné tváre sú navzájom rovnobežné. Je to bežný polyhedrón v našom každodennom živote, pretože ho môžeme nájsť v škatuliach topánok, tvar tehly, tvar mikrovlnnej rúry atď.

Ako polyhedrón, paralelnepiped obsahuje konečný objem a všetky jeho tváre sú ploché. Je súčasťou skupiny hranolov, ktoré sú tie polyhedry, v ktorých sú všetky jeho vrcholy obsiahnuté v dvoch paralelných rovinách.

Prvky paralelnepiped

Tváre

Sú každá z oblastí tvorených rovnobežníkmi, ktoré obmedzujú paralepiped. ParalePiped má šesť tvárí, kde každá tvár má štyri susedné tváre a opak. Okrem toho je každá tvár rovnobežná s jej opakom.

Perspektíva paralelnepipovaného

Hrany

Sú spoločnou stránkou dvoch tvárí. Celkovo má paralelnepiped dvanásť hrán.

Vrchol

Je to bežný bod troch tvárí, ktoré susedia s dvoma až dvoma. ParalePiped má osem vrcholov.

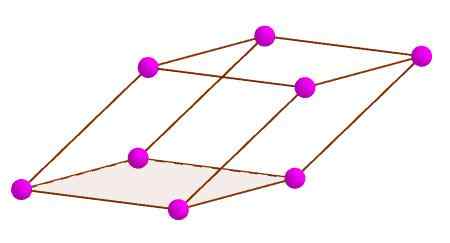Vrcholy paralelnepiped

Diagonálny

Vzhľadom na dve tváre rovnobežky oproti sebe, môžeme nakresliť segment čiary, ktorý prechádza z vrcholu jednej tváre k protiľahlému vrcholu druhého.

Tento segment je známy ako paralelnepipovaná uhlopriečka. Každý paralelnepiped má štyri diagonály.

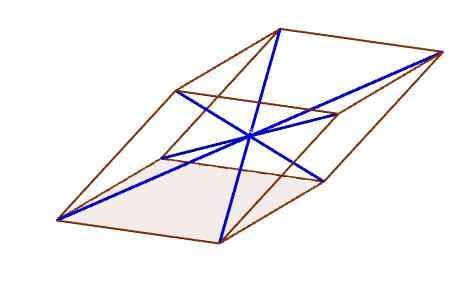Diagonály paralelnepiped

Stred

Je to bod, v ktorom sa pretínajú všetky diagonály.

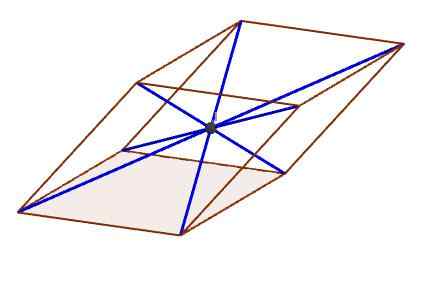Bod na obrázku označuje stred, kde sa pretínajú všetky diagonály

Charakteristiky paralelnepiped

Ako sme už spomenuli, toto geometrické telo má dvanásť hrán, šesť tvárí a osem vrcholov.

V paralepipite je možné identifikovať tri sady tvorené štyrmi hranami, ktoré sú navzájom rovnobežné. Okraje týchto súborov navyše dodržiavajú vlastnosť s rovnakou dĺžkou.

Charakteristiky paralelnepiped

Predstavuje ďalšiu nehnuteľnosť.

Okrem toho paralelnepipeds, ktoré sú vypuklé polyhedros, sú v súlade s Eulerovou vetou pre polyhedros, ktorá nám dáva vzťah medzi počtom tvárí, počtom hrán a počtom vrcholov. Tento vzťah je uvedený vo forme nasledujúcej rovnice:

C + V = A + 2

Táto vlastnosť je známa ako Eulerova charakteristika. Kde C je počet tvárí a počet vrcholov a počet hrán.

Typy paramelníkov

Môžeme klasifikovať paralellepípedos na základe ich tvárí, podľa nasledujúcich typov:

Ortoedro

Sú to paralellepípedos, kde sú ich tváre vyrobené zo šiestich obdĺžnikov. Každý obdĺžnik je kolmý s tými, s ktorými zdieľa Edge. Sú najbežnejšie v našom každodennom živote, toto je obvyklá forma topánok a tehlových škatúľ.

Ortoedro rovnobežný

Pravidelná kocka alebo Hexaedro

Toto je konkrétny prípad predchádzajúceho, kde každá z tvárí je štvorec.

Môže vám slúžiť: EllipsePravidelná kocka alebo Hexaedro

Kocka je tiež súčasťou geometrických telies nazývaných platonické tuhé látky. Platonická tuhá látka je konvexný polyhedron, takže jeho tváre aj vnútorné uhly sú navzájom rovnaké.

Romboedro

Je to paralelnepiped, ktorý má kosto. Všetky tieto kostry sú navzájom rovnaké, pretože zdieľajú hrany.

Romboedro

Romboiedro

Jeho šesť tvárí je rhomboid. Pripomeňme, že rhomboid je štvorčlenný polygón a štyri uhly, ktoré sú rovnaké dva až dva. Rhomboidy sú rovnobežky, ktoré nie sú ani štvorcové, ani obdĺžniky, ani kosoštvorcami.

Romboiedro

Na druhej strane, šikmé paralelnepipeds sú tie, v ktorých sa aspoň jedna výška nezhoduje s jej okrajom. V tejto klasifikácii môžeme zahrnúť Rhomboedros a Rhomboiedros.

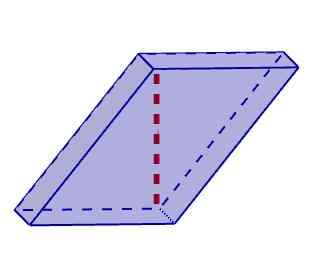Šikmý paralelnepipovaný

Výpočet

Na výpočet diagonálu ortoedra môžeme použiť vetu Pythagora pre r³.

Pripomeňme, že ortoedro má charakteristiku, že každá strana je kolmá so stranami, ktoré zdieľa Edge. Z tejto skutočnosti môžeme zistiť, že každá hrana je kolmá s tými, ktoré zdieľa vrchol.

Na výpočet dĺžky diagonálu ortoedro postupujeme takto:

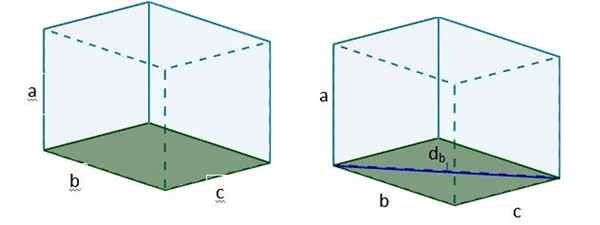
1. Vypočítame uhlopriečku jednej z tvárí, ktoré vložíme podľa základne. Na tento účel používame vetu Pythagoras. Pomenujme ten diagonálny D_b.

2. Potom s D_b Môžeme vytvoriť nový obdĺžnikový trojuholník, takže hypotenus uvedeného trojuholníka je hľadaný diagonálny D.

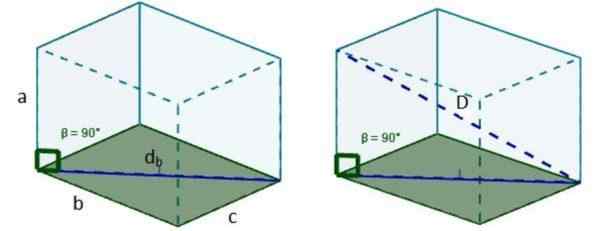
3. Pythagoras vetu znova používame a máme, že dĺžka tejto uhlopriečky je:

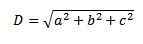
Ďalším spôsobom, ako vypočítať diagonálne grafickejšie, je súčet voľných vektorov.

Pripomeňme, že dva voľné vektory A a B sa pridávajú umiestnením chvosta vektora B špičkou vektora a.

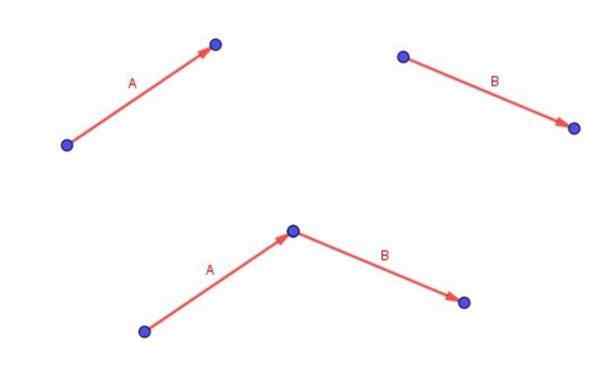
Vektor (a + b) je ten, ktorý začína v chvoste a a končí na špičke b.

Zvážte paralelnepiped, na ktorý chceme vypočítať diagonál. Hrany identifikujeme pomocou vhodných orientovaných vektorov.

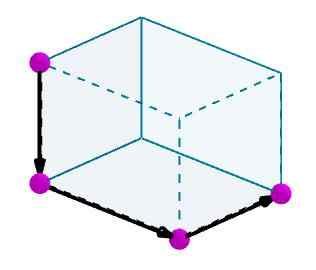
Potom pridáme tieto vektory a výsledný vektor bude diagonálnym paralepipedom.

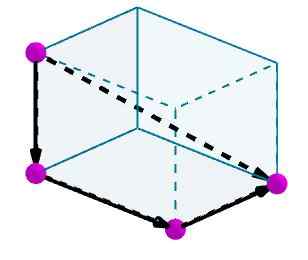
Plocha paralelnepiped

Oblasť paralelnepiped je daná súčtom každej z oblastí jeho tvárí.

Ak určíme jednu zo strán ako základňu,

Do_L + Druhý_B = Celková plocha

Kde_L Sa rovná súčtu oblastí všetkých strán susediacich so základňou, nazývanou bočná oblasť a_B Je to základná oblasť.

V závislosti od typu paralelnepiped, s ktorým pracujeme, môžeme prepísať uvedený vzorec.

Oblasť ortoedro

Je daný vzorcom

A = 2 (AB + BC + CA).

Príklad 1

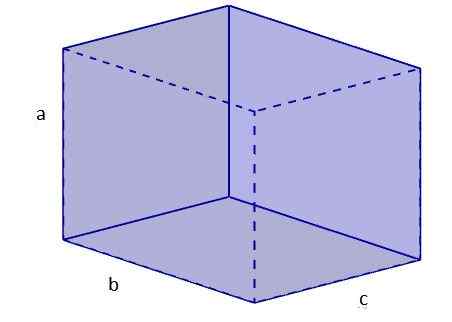
Vzhľadom na nasledujúce ortoedro, so stranami A = 6 cm, b = 8 cm a c = 10 cm, vypočítajte plochu paralepippitu a dĺžku jej diagonálu.

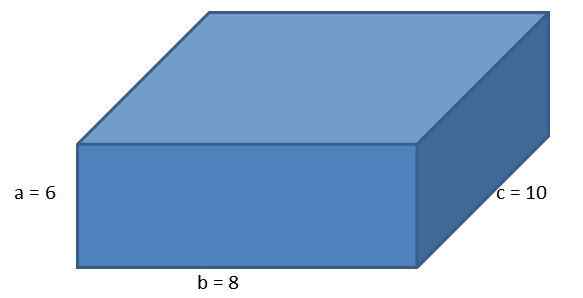
Pomocou vzorca pre oblasť ortoedra musíme

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Všimnite si, že ako ortoedro je dĺžka ktorejkoľvek zo svojich štyroch diagonálov rovnaká.

Môže vám slúžiť: Neurčitý integrál: Vlastnosti, aplikácie, výpočet (príklady)

Použitie vety Pythagory pre priestor musíme

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Oblasť kocky

Pretože každá hrana má rovnakú dĺžku, máme to a = b a a = c. Nahradenie v predchádzajúcom vzorci, ktorý máme

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6a²

Príklad 2

Krabica hernej konzoly má tvar kocky. Ak chceme zabaliť túto krabicu darčekovým papierom, koľko papiera by sme utratili vedomím, že dĺžka hrán kocky je 45 cm?

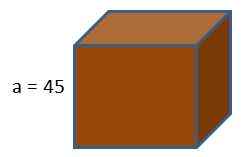
Použitím vzorca oblasti kocky sa dostaneme

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Oblasť Rhomboedro

Pretože všetky jeho tváre sú rovnaké, stačí vypočítať plochu jedného z nich a vynásobte ju šiestimi.

Máme, že oblasť kostra sa dá vypočítať pomocou jej diagonálov s nasledujúcim vzorcom

Do_R = (Dd)/2

Použitím tohto vzorec vyplýva, že celková plocha rhomboedro je

Do_Tón = 6 (dd)/2 = 3DD.

Príklad 3

Tváre nasledujúceho rhomboedra sú tvorené rhombusom, ktorého diagonálne sú d = 7 cm a d = 4 cm. Vaša oblasť bude

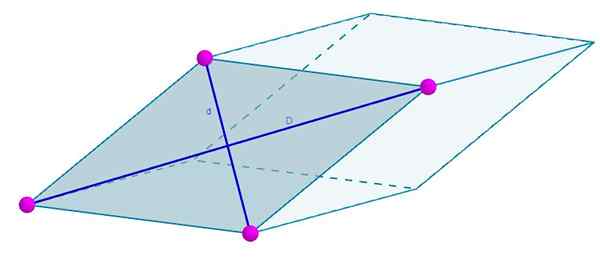
A = 3 (7 cm) (4 cm) = 84 cm².

Oblasť Rhomboiedro

Na výpočet plochy rhomboiedra musíme vypočítať plochu rhomboidov, ktoré ju skladajú. Keďže paralelnepipeds plnia vlastnosť, že opačné strany majú rovnakú oblasť, môžeme priradiť boky do troch rovesníkov.

Týmto spôsobom máme, že vaša oblasť bude

Do_Tón = 2B₁h₁ + 2B₂h₂ + 2B₃h₃

Kde b_Jo sú základy spojené so stranami a h_Jo jeho relatívna výška zodpovedajúca uvedeným základom.

Príklad 4

Zvážte nasledujúce paralelnepiped,

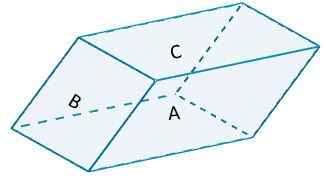
kde strana A a strana A '(ich opačná strana) sú založené na b = 10 a na výšku h = 6. Označená oblasť bude mať hodnotu

Do₁ = 2 (10) (6) = 120

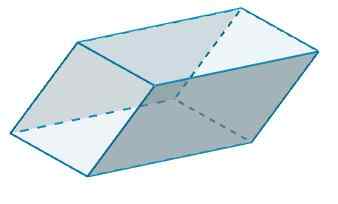
B a b 'majú b = 4 a h = 6, potom

Do₂ = 2 (4) (6) = 48

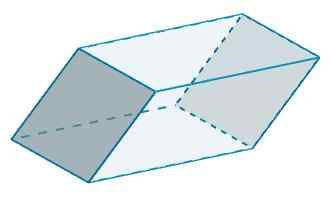
A c a c 'majú b = 10 a h = 5,

Do₃ = 2 (10) (5) = 100

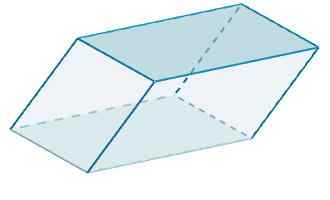
Nakoniec oblasť Rhomboiedro je

A = 120 + 48 + 100 = 268.

Objem paralelnepipovaných

Vzorec, ktorý nám dáva objem paralelnepiped, je produktom oblasti jednej z jeho tvárí kvôli výške zodpovedajúcej uvedenej tváre.

V = a_Ch_C

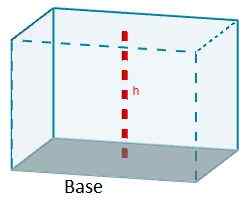
V závislosti od typu paralelnepiped je možné tento vzorec zjednodušiť.

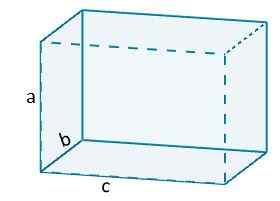
Preto máme napríklad, že objem ortoedro by bol daný

V = ABC.

Kde A, B a C predstavujú dĺžku hrán Orthoedro.

Av konkrétnom prípade kocky je

V = a³

Príklad 1

Existujú tri rôzne modely pre škatule cookie a chcete.

Prvým je kocka, ktorej okraj má dĺžku a = 10 cm.

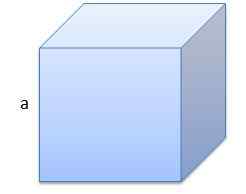
Jeho objem bude v = 1000 cm³

Druhý je b = 17 cm, c = 5 cm, d = 9 cm.

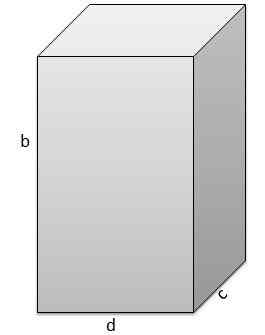
A preto je jeho objem V = 765 cm³

A tretí má e = 9 cm, f = 9 cm a g = 13 cm.

A jeho objem je v = 1053 cm³

Môže vám slúžiť: typy uhlov, charakteristík a príklady

Preto je políčka s najväčším objemom tretí.

Ďalšou metódou na získanie objemu paralelnepipsu je uchýlenie sa k vektorovej algebre. Najmä trojitý skalárny produkt.

Jednou z geometrických interpretácií trojitého skalárneho produktu je objem paralepipiped, ktorého okraje sú tri vektory, ktoré zdieľajú rovnaký vrchol ako východiskový bod.

Týmto spôsobom, ak máme paralelnepiped a chceme vedieť, aký je jeho objem, stačí ho reprezentovať v súradnicovom systéme v r³ zhodujúci sa s jedným z jeho vrcholov s pôvodom.

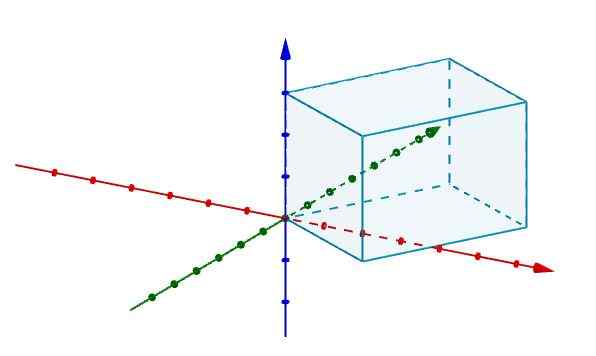
Potom predstavujeme okraje, ktoré sa zhodujú s pôvodom vektormi, ako je to znázornené na obrázku.

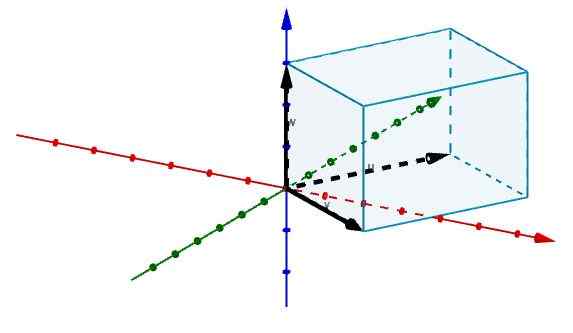
A týmto spôsobom máme, že objem uvedených paralelnepiped je daný

V = | Axb ∙ C |

Alebo ekvivalent, objem je determinant matice 3 × 3, tvorená komponentmi okrajových vektorov.

Príklad 2

Predstavením nasledujúceho paralelnepipiped v r³ Vidíme, že vektory, ktoré to určujú, sú nasledujúce

u = (-1, -3,0), v = (5, 0, 0) a w = (-0.25, -4, 4)

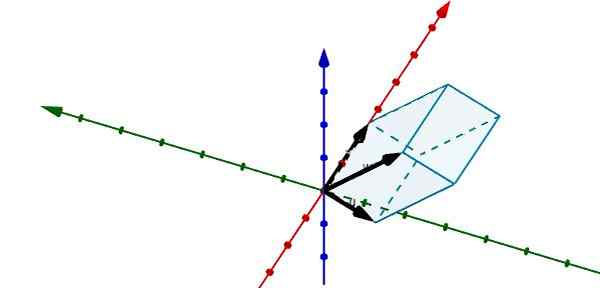
Používanie trojnásobného skalárneho produktu, ktorý máme

V = | (UXV) ∙ W |

Uxv = (-1, -3,0) x (5, 0, 0) = (0,0, -15)

(Uxv) ∙ w = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

To dospelo k záveru, že v = 60

Zvážte teraz nasledujúce paralelnepipiped v R³ ktorých okraje sú určené vektormi

A = (2, 5, 0), b = (6, 1, 0) a c = (3, 4, 4)

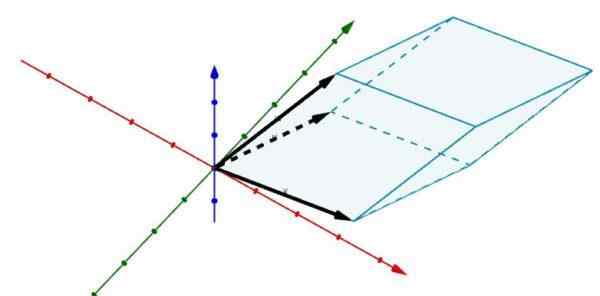
Používanie determinantov nám to dáva

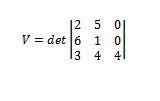
Máme teda, že objem uvedených paralelnepiped je 112.

Oba sú rovnocenné spôsoby výpočtu objemu.

Perfektný paralepipiped

Je známa ako Euler Brick (alebo Euler Block) do ortoedro, ktorý spĺňa vlastnosť, že dĺžka jeho hrán a dĺžka diagonálov každej z jeho tvárí sú celé čísla.

Zatiaľ čo Euler nebol prvým vedcom, ktorý študoval ortoeders, ktorí sa stretávajú s týmto majetkom, našiel o nich zaujímavé výsledky.

Najmenšia tehla Eulera objavila Paul Halcke (1662-1731) a dĺžky jej hrán sú a = 44, b = 117 a c = 240.

Otvorený problém v teórii čísel je nasledujúci:

Existujú dokonalí ortoeders?

V súčasnosti táto otázka stále nemá odpoveď, pretože nebolo možné dokázať, že neexistujú žiadne telá, ale nikto nebol nájdený.

Doteraz sa preukázalo, že dokonalé paralepiped do. Prvý, ktorý sa objaví, má ako dĺžku jeho okrajov hodnoty 103, 106 a 271.

Odkazy

1. Chlap, r. (1981). Nevyriešené problémy v teórii čísel. Prubár.
2. Landaverde, f. d. (1997). Geometria. Pokrok.
3. Leithold, L. (1992). Výpočet analytickou geometriou. Harla, s.Do.
4. Rendon, a. (2004). Technická výkres: Notebook aktivity 3 2. bakalár. Tebar.
5. Resnick, r., Halliday, D., & Krane, K. (2001). Fyzika zväzku. 1. Mexiko: kontinentálne.