Definícia, vlastnosti a príklady hyperbolického paraboloidu

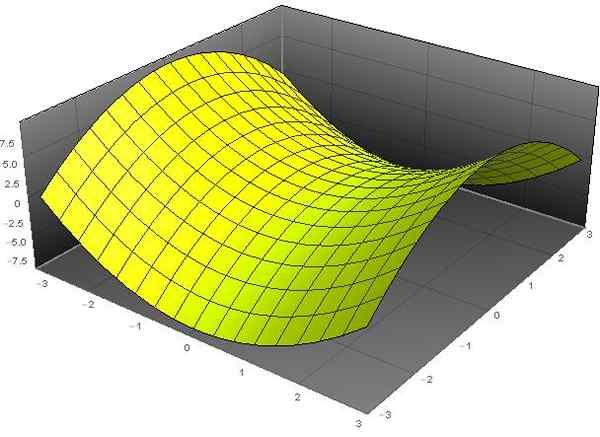
A hyperbolidový paraboloid Je to povrch, ktorého všeobecná rovnica v karteziánskych súradniciach (x, y, z) spĺňa nasledujúcu rovnicu:

(pre)² - (a/b)² - Z = 0.

„Paraboloidná“ nominálna hodnota vychádza zo skutočnosti, že premenná Z závisí od štvorcov premenných X a Y. Zatiaľ čo prídavné meno „hyperbolické“ je spôsobené skutočnosťou, že rovnica hyperboly má pevné hodnoty Z. Tvar tohto povrchu je podobný tvaru stoličky na koni koňa.

postava 1. Hyperbolický paraboloid z = x² - a². Zdroj: f. Zapata cez Wolfram Mathematica.

[TOC]

Opis hyperbolického paraboloidu

Aby sme pochopili povahu hyperbolického paraboloidu, bude vykonaná nasledujúca analýza:

1.- Konkrétny prípad bude prijatý a = 1, b = 1, to znamená, že karteziánska rovnica paraboloidu zostáva ako z = x² - a².

2.- Považujú sa za paralelné roviny s rovinou ZX, tj y = ctte.

3.- S y = ctte je to z = x² - C, ktorý predstavuje podobenstvá s vetvami hore a vrcholom pod rovinou XY.

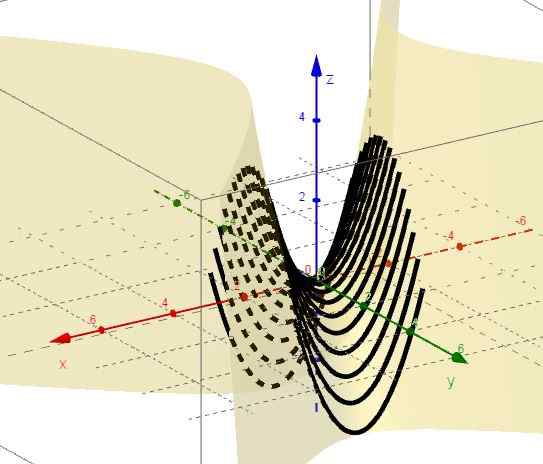Obrázok 2. Rodina kriviek z = x² - C. Zdroj: f. Zapata cez geogebra.

4.- S x = ctte je z = c - y², ktorý predstavuje podobenstvá s vetvami dole a vrcholom nad rovinou XY.

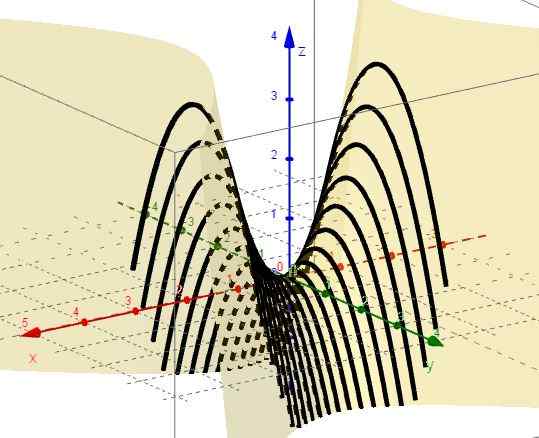Obrázok 3. Rodina kriviek z = c - a². Zdroj: f. Zapata cez geogebra.

5.- S z = ctte je c = x² - a², ktoré predstavujú hyperboly v rovinách rovnobežných s rovinou XY. Keď C = 0 sú dve čiary (A +45 ° a -45 ° vzhľadom na os x), ktoré sú zachytené na pôvode v rovine xy.

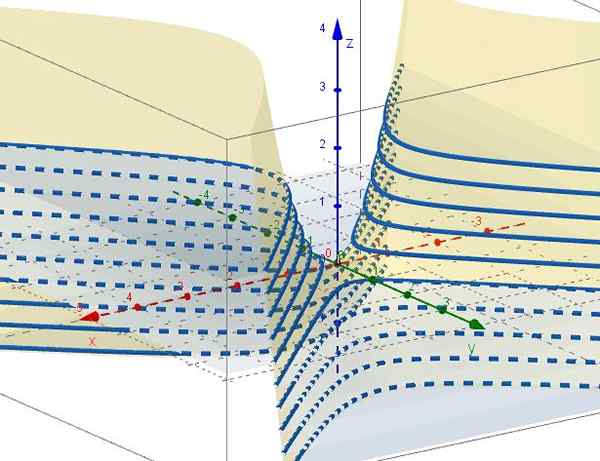Obrázok 4. Rodina kriviek x² - a² = C. Zdroj: f. Zapata cez Geogebra ..

Vlastnosti hyperbolického paraboloidu

1.- Štyri rôzne body v trojrozmernom priestore definujú jeden a iba hyperbolický paraboloid.

Môže vám slúžiť: obmedzte vlastnosti (s príkladmi)

2.- Hyperbolický paraboloid je a dvojitý regulovaný povrch. To znamená, že napriek tomu, že ide o zakrivený povrch, pre každý bod hyperbolického paraboloidu dva rôzne línie úplne prechádzajú do hyperbolického paraboloidu. Druhý povrch, ktorý nie je rovinou a je dvojnásobne regulovaný, je Revolúcia hyperboloid.

Presne je to druhá vlastnosť hyperbolického paraboloidu, ktorá ho umožnila široké použitie v architektúre, pretože povrch je možné generovať z lúčov alebo rovných reťazcov.

Druhá vlastnosť hyperbolického paraboloidu umožňuje jeho alternatívnu definíciu: Je to povrch, ktorý môže byť generovaný priamou mobilnou čiarou rovnobežnou s pevnou rovinou a rezať dve pevné čiary, ktoré slúžia ako vodítko. Nasledujúci obrázok objasňuje túto alternatívnu definíciu hyperbolického paraboloidu:

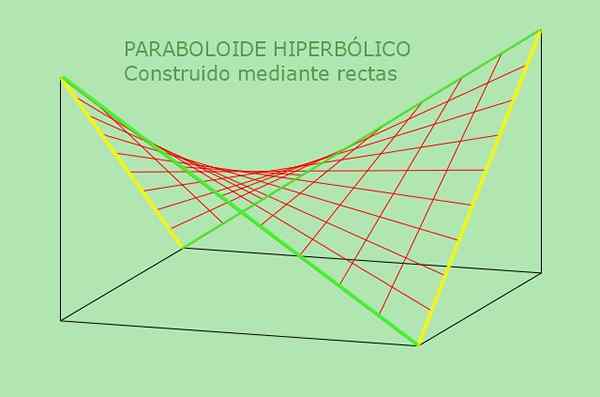Obrázok 5. Hyperbolický paraboloid je dvojnásobne regulovaný povrch. Zdroj: f. Zapata.

Vyriešené príklady

- Príklad 1

Preukázať, že rovnica: Z = xy, zodpovedá hyperbolickému paraboloidu.

Riešenie

Transformácia sa použije v premenných X a Y zodpovedajúce rotácii karteziánskych osí vzhľadom na os +45 osi. Staré súradnice X a Y sa transformujú na nový X 'E a' podľa nasledujúcich vzťahov:

x = x ' - y'

y = x ' + a'

Kým súradnica Z zostáva rovnaká, to je z = z '.

Nahradením v rovnici z = x a máme:

z '= (x' - y ') (x' + y ')

Pri aplikácii pozoruhodného produktu rozdielu súčtom rovnajúcou sa rozdielom štvorcov je:

Z '= x'² - a '²

čo jasne zodpovedá definícii pôvodne uvedenej hyperbolického paraboloidu.

Odpočúvanie rovín rovnobežných s osou xy s hyperbolickým paraboloidom z = x a určte rovnostranné hyperboly, ktoré majú asymptoty roviny x = 0 e y = 0.

Môže vám slúžiť: Miletus takúto vetu

- Príklad 2

Určiť parametre do a b hyperbolického paraboloidu, ktorý prechádza bodmi A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) a D (2, -1, 32/9).

Riešenie

Podľa svojich vlastností určujú štyri body v trojrozmernom priestore jediný hyperbolický paraboloid. Všeobecná rovnica je:

Z = (x/a)² - (a/b)²

Nahrádzame dané hodnoty:

Pre bod a máte 0 = (0/a)² - (0/b)², rovnica, ktorá je splnená bez ohľadu na hodnoty parametrov a a b.

Výmena bodu B sa získa:

5/9 = 1/a² - 1 b²

Zatiaľ čo pre bod C zostáva:

32/9 = 4/a² - 1 b²

Nakoniec, pre bod D sa získa:

32/9 = 4/a² - 1 b²

Čo je totožné s predchádzajúcou rovnicou. Stručne povedané, systém rovníc by sa mal vyriešiť:

5/9 = 1/a² - 1 b²

32/9 = 4/a² - 1 b²

Odčítanie druhej rovnice prvej sa získa:

27/9 = 3/a² čo to znamená² = 1.

Podobne sa odpočítava druhá rovnica štvornásobného prvého

(32-20)/9 = 4/a² - 4/a² -1 b² + 4/b²

Zjednodušilo sa to ako:

12/9 = 3/b² ⇒ b² = 9/4.

Stručne povedané, hyperbolický paraboloid, ktorý prechádza cez body A, B, C a D, má karteziánsku rovnicu danú:

Z = x² - (4/9) a²

- Príklad 3

Podľa vlastností hyperbolického paraboloidu, dve čiary, ktoré sú v ňom úplne obsiahnuté pre každý bod. V prípade z = x^2 - y^2 Nájdite rovnicu dvoch riadkov, ktoré prechádzajú bodom P (0, 1, -1) jasne patriace k hyperbolickému paraboloidu, takže všetky body týchto riadkov patria aj do istota.

Riešenie

Pomocou pozoruhodného produktu rozdielu v štvorci je možné rovnicu hyperbolického paraboloidu napísať nasledovne:

Môže vám slúžiť: štvornásobné: prvky, vlastnosti, klasifikácia, príklady

(x + y) (x - y) = c z (1/c)

Kde C je nenálová konštanta.

Rovnica x + y = c z a rovnica x - y = 1/c zodpovedajú dvom rovinám s normálnymi vektormi n= y m=. Vektorový produkt m x n = Smer priesečníka liniek týchto dvoch rovín nám dáva. Potom jedna z riadkov, ktorá prechádza bodom P a patrí do hyperbolického paraboloidu, má parametrickú rovnicu:

= + t

Aby sme určili C, nahradíme bod P v rovnici x + y = c z, získanie:

C = -1

Podobne, ale vzhľadom na rovnice (x - y = k z) a (x + y = 1/k) máte parametrickú rovnicu riadku:

= + s s k = 1.

Stručne povedané, dva riadky:

= + t y = + s

Sú úplne obsiahnuté v hyperbolickom paraboloidnom z = x² - a² Prechádzanie bodom (0, 1, -1).

Ako kontrola predpokladajte, že t = 1, čo nám dáva bod (1,2, -3) na prvom riadku. Musíte skontrolovať, či je tiež na paraboloidnom z = x² - a²:

-3 = 1² - 2² = 1 - 4 = -3

Čo potvrdzuje, že v skutočnosti patrí na povrch hyperbolického paraboloidu.

Hyperbolický paraboloid v architektúre

Obrázok 6. Oceanographic of Valencia (Španielsko).Zdroj: Wikimedia Commons.

Hyperbolický paraboloid používali v architektúre veľkí avantgardní architekti, medzi ktorými sú mená španielskeho architekta Antoniho Gaudího (1852-1926) a veľmi najmä španielsky aj španielsky Félix Candela (1910-1997) veľmi obzvlášť.

Nižšie sú uvedené niektoré diela založené na hyperbolickom paraboloide:

-Kaplnka mesta Cuernavaca (Mexiko) Práca architekta Félix Candela.

-Oceánografický Valencia (Španielsko), tiež Félix Candela.

Odkazy

1. Encyklopédia matematiky. Vládny povrch. Získané z: Encyclopediaofmath.orgán
2. Llera rubén. Hyperbolidový paraboloid. Získané z: Rubenllera.Slovník.com
3. Weisstein, Eric W. „Hyperbolický paraboloid.”Z webového zdroja Mathworld-A Wolfram. Obnovené z: Mathworld.Valfram.com
4. Wikipedia. Paraboloidný. Zdroj: In.Wikipedia.com
5. Wikipedia. Paraboloidný. Obnovené z: je.Wikipedia.com
6. Wikipedia. Vládny povrch. Zdroj: In.Wikipedia.com