Základná veta aritmetických demonštrácií, aplikácií, cvičení

On Základná veta aritmetiky Uvádza, že akékoľvek prirodzené číslo väčšie ako 1 sa dá rozdeliť ako produkt prvých čísel - drží niektoré - a táto forma je pre toto číslo jedinečná, hoci poradie faktorov sa môže líšiť.

Pamätajte, že hlavné číslo p Je to ten, ktorý pripúšťa iba ako pozitívny deliaci a 1. Nasledujúce čísla sú bratranci: 2, 3, 5, 7, 11, 13 a tak ďalej, pretože sú nekonečné. Číslo 1 sa nepovažuje za bratranec za to, že má jediného deliteľa.

postava 1. Euclides (vľavo) demonštroval základnú vetu aritmetiky vo svojich knižných prvkoch (350 a.C.) A prvá úplná demonštrácia je spôsobená Carl f. Gauss (1777-1855) (vpravo). Zdroj: Wikimedia Commons.

Pokiaľ ide o ich časť, nazývajú sa čísla, ktoré nespĺňajú vyššie uvedené zložené čísla, AS 4, 6, 8, 9, 10, 12, 14 ... Vezmime napríklad číslo 10 a okamžite uvidíme, že ho možno rozdeliť ako produkt 2 a 5:

10 = 2 × 5

2 a 5 sú skutočne hlavné čísla. Veta uvádza, že je to možné pre ľubovoľné číslo n:

Kde p₁, p₂, p₃… P_r Sú to prvotné čísla a k₁, klimatizovať₂, klimatizovať₃,... k_r Sú to prirodzené čísla. Takže prvotné čísla sa správajú ako tehly, z ktorých sú vybraním vytvorené prírodné čísla.

[TOC]

Demonštrácia základnej vety aritmetiky

Začína demonštrovať, že každé číslo sa môže rozložiť v hlavných faktoroch. Byť prírodným číslom n> 1, bratranec alebo zlúčeniny.

Napríklad ak n = 2, dá sa vyjadriť ako: 2 = 1 × 2, ktorým je bratranec. Rovnakým spôsobom pokračujeme v nasledujúcich číslach:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Pokračujeme takto, rozkladáme všetky prírodné čísla, až kým nedosiahneme číslo n -1. Uvidíme, či to dokážeme s nasledujúcim číslom: n.

Ak n je bratranec, môžeme ho rozložiť ako n = 1 × n, ale predpokladáme, že n je zložený a má deliteľ d, logicky menej ako n:

Môže vám slúžiť: Opisná štatistika: História, charakteristiky, príklady, koncepty

1< d < n.

ÁNO N/D = P₁, s p₁ Číslo prvočísla, potom n je napísané ako:

n = p₁.d

Ak D je bratranec, nie je čo robiť, ale ak nie, existuje číslo n₂ čo je deliteľ d a menej ako toto: n₂ < d, por lo que d podrá escribirse como el producto de n₂ Pre ďalšie číslo bratranca P₂:

d = p₂ n₂

Že nahradením pôvodného čísla n by poskytlo:

n = p₁ .p₂ .n₂

Teraz predpokladajme n₂ Ani to nie je prvotné číslo a píšeme ho ako produkt prvočísla p₃, pre jeho deliteľa₃, tak, že n₃ < n₂ < n₁ < n:

n₂ = p₃.n₃ → n = P₁ p₂ p₃.n₃

 Túto procedúru opakujeme konečným počtomkrát, kým nedostanete:

n = p₁.p₂.p₃ … P_r

To znamená, že je možné rozložiť všetky celé čísla z 2 na číslo N, ako produkt prvých čísel.

Jedinečnosť rozkladu v hlavných faktoroch

Overmeme teraz, že s výnimkou poradia faktorov je tento rozklad jedinečný. Predpokladajme, že môžete písať dvoma spôsobmi:

n = p₁.p₂.p₃ … P_r = q_1.Otázka₂.Otázka₃... Otázka_siež  (s r ≤ s)

Samozrejme q₁, Otázka₂, Otázka₃... Sú to tiež prvotné čísla. Ako p₁ rozdeliť na (q_1.Otázka₂.Otázka₃... Otázka_siež) Potom P₁ Je to rovná sa s ktorýmkoľvek z „q“, bez ohľadu na to Čo, takže môžeme povedať, že P₁ = q₁. Rozdelíme n medzi p₁ A dostaneme:

p₂.p₃ … P_r =_.Otázka₂.Otázka₃... Otázka_siež

Opakujeme postup rozdeliť všetko medzi P_r, Potom dostaneme:

1 = q_R+1... Otázka_siež

Ale nie je možné sa dostať k q_R+1... Otázka_siež = 1 Keď r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Žiadosti

Ako sme už povedali, hlavné čísla predstavujú, ak chcete, atómy čísel, ich základné komponenty. Takže základná veta aritmetiky má početné aplikácie, najzreteľnejšie: Môžeme ľahšie pracovať s veľkým počtom, ak ich vyjadríme ako produkt menších čísel.

Môže vám slúžiť: celé čísla

Rovnakým spôsobom nájdeme maximálny spoločný násobok (m.c.m.) a maximálny spoločný deliteľ (m.C.D.), Postup, ktorý nám pomáha ľahšie robiť sumy frakcií, nájsť korene veľkého počtu alebo pracovať s radikálmi, racionalizovať a riešiť problémy s aplikáciou veľmi rozmanitej povahy.

Okrem toho sú hlavné čísla mimoriadne záhadné. Vzor sa v nich ešte neuznáva a nie je možné vedieť, čo bude nasledujúce. Najväčšie, kým sa počítače nenašli a má 24.862.048 ciferník, Aj keď sa nové prvočné čísla objavujú zakaždým menej často.

Primo čísla v prírode

Cicadas, Cycaked alebo Chicharras žijúci na severovýchode Spojených štátov sa objavia v 13 alebo 17 -ročných cykloch. Obidve sú prvotné čísla.

Týmto spôsobom sa Chicharras vyhýba zhodujúcim sa s predátormi alebo konkurentmi, ktorí majú iné obdobia pôrodu, ani rôzne odrody Chicharra súťažia medzi sebou, pretože sa v tom istom roku nezhodujú.

Obrázok 2. Kúzelníky Cicada del Este v Spojených štátoch sa objavuje každých 13 alebo 17 rokov. Zdroj: pxfuel.

Primo čísla a online nákupy

Čísla Primo sa používajú v kryptografii na uchovávanie podrobností o kreditných kartách pri nákupe online nákupov. Týmto spôsobom údaje, ktoré kupujúci prichádza presne do obchodu, bez straty alebo upadnutia do bezohľadných ľudí.

Ako? Údaje o kartách sú kódované v čísle n, ktoré je možné vyjadriť ako produkt prvých čísel. Tieto hlavné čísla sú kľúčom, ktorý odhaľuje údaje, ale nie sú pre verejnosť známe, môžu sa dekódovať iba na webe, na ktorý sú nasmerované.

Rozloženie čísla do faktorov je ľahká úloha, ak sú čísla malé (videnie vyriešených cvičení), ale v tomto prípade sa používajú ako kľúčové hlavné čísla 100 číslic, ktoré ich vynásobením poskytujú oveľa väčšie čísla, ktorých podrobný rozklad znamená obrovská práca.

Môže vám slúžiť: Prebužný odhad

Vyriešené cvičenia

- Cvičenie 1

Rozložiť 1029 do hlavných faktorov.

Riešenie

1029 je deliteľné 3. Je to známe, pretože pridaním číslic je súčet násobku 3: 1+0+2+9 = 12. Pretože poradie faktorov nemení produkt, môžeme tam začať:

1029 3

343

1029 = 3 × 343

Na druhej strane 343 = 7³, tak:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

A keďže 3 aj 7 sú prvotné čísla, je to rozklad 1029.

- Cvičenie 2

Faktor trinomial x² + 42x + 432.

Riešenie

Trinomial je prepísaný vo forme (x+a). (x+b) a musíme nájsť hodnoty a a b, takže:

A+B = 42; do.B = 432

Číslo 432 sa rozkladá na hlavné faktory a odtiaľ je vybraný Tanteom, vhodná kombinácia skutočností pridaných do 42.

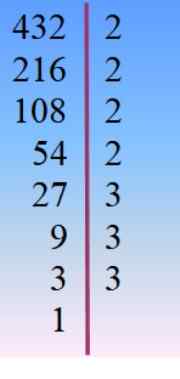
432 = 2⁴ × 3³ = 23³× 2³ = 2⁴× 3² × 3 =…

Odtiaľ existuje niekoľko možností napísať 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72… .

A všetky sa dajú nájsť kombináciou produktov medzi hlavnými faktormi, ale na vyriešenie navrhovaného cvičenia je jedinou primeranou kombináciou: 432 = 24 × 18 od 24 + 18 = 42, potom:

X² + 42x + 432 = (x + 24). (x +18)

Odkazy

1. Baldor, a. 1986. Praktický teoretický aritmetický. Editor Kultúrna spoločnosť amerických textov s.Do.
2. Svet BBC. Skrytý prírodný kód. Zdroj: BBC.com.
3. Z Leon, Manuel.Primo čísla: internetoví strážcovia. Obnovené z: blogov.20 minút.je.
4. Žobrák. Teória čísel I: Základná veta aritmetiky. Zdroj: Teoriadenumeros.Wikidot.com.
5. Wikipedia. Základná veta aritmetiky. Obnovené z: je.Wikipedia.orgán.