Orthoedro vzorce, oblasť, objem, diagonálne, príklady

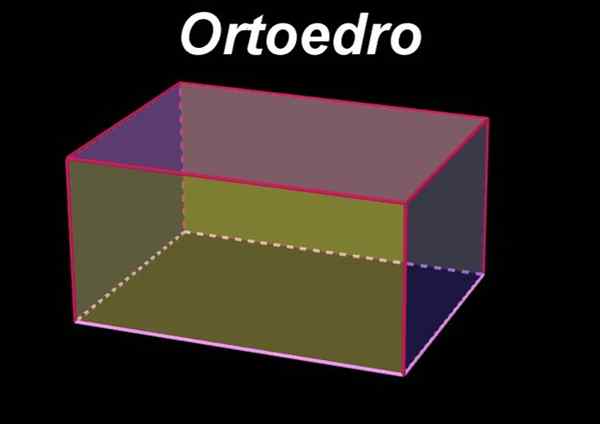
On Ortoedro Je to objemová alebo trojrozmerná geometrická postava, ktorá je charakterizovaná šiestimi obdĺžnikovými tvárami, takže opačné tváre sú v paralelných rovinách a sú rovnaké alebo zhodné obdĺžniky medzi sebou. Na druhej strane, tváre susediace s danou tvárou sú v rovinách kolmých na pôvodnú tvár.

Dá sa tiež zvážiť, kedy Ortoedro ako ortogonálny pravouhlý základný hranol, v ktorom uhly Dihedros Tvorované dvoma plánymi vedenými v susedstve spoločnej hrany merajú 90 °. Dihedrálny uhol medzi dvoma tvárami sa meria na križovatke tvárí so kolmou a spoločnou rovinou pre nich.

postava 1. Ortoedro. Zdroj: f. Zapata s geogebou.

Podobne je ortoedro obdĺžnik rovnobežný, Pretože je to definované na paralepipiped ako objemovú postavu šiestich tvárí, ktoré sú rovnobežné dve s dvoma.

V akomkoľvek rovnobežných plochách sú tváre rovnobežníky, ale v obdĺžniku musia byť tváre obdĺžnikové tváre obdĺžnikové.

[TOC]

Časti Orthoedro

Časti polyhedronu, napríklad ortoedro, sú:

-Hrany

-Vrcholy 

-Tváre

Uhol medzi dvoma okrami tváre ortoedro sa zhoduje s dihedrálnym uhlom tvorenými jeho ostatnými dvoma tvárami susediacimi s každou z okrajov a tvoria pravý uhol. Nasledujúci obrázok objasňuje každý koncept:

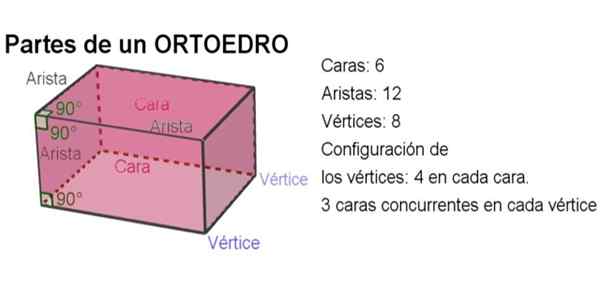Obrázok 2. Časti ortoedra. Zdroj: f. Zapata s geogebou.

-Celkovo má ortoedro 6 tvárí, 12 hrán a 8 vrcholov.

-Uhol medzi dvoma hranami je pravý uhol.

-Dihedrálny uhol medzi akýmikoľvek dvoma stranami je tiež rovný.

-V každej tvári sú štyri vrcholy a v každom vrchole sa zúčastňujú tri vzájomne ortogonálne tváre.

Môže vám slúžiť: Čo je číslo capicúa? Vlastnosti a príklady

Ortoedro vzorce

Oblasť

Povrch alebo plocha a Ortoedro Je to súčet oblastí ich tvárí.

Ak majú tri okraje, ktoré sa zhodujú vo vrchole Clek A tvár na pozadí má tiež oblasť CQB.

Potom majú dve bočné tváre oblasť Ark každý. A nakoniec, tváre podlahy a strechy majú plochu Ark každý.

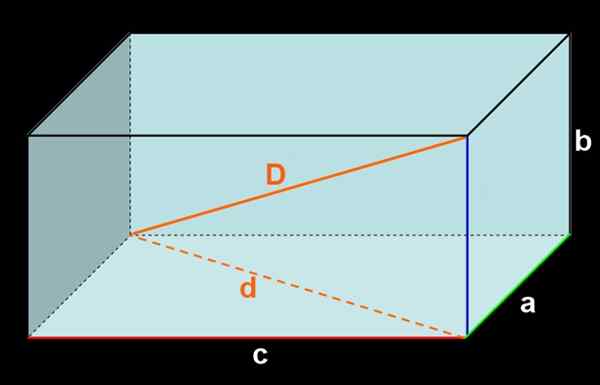Obrázok 3. Orthoedro rozmerov A, B, C. Vnútorná diagonálna D a vonkajšia diagonálna D.

Získa sa oblasť všetkých tvárí:

A = 2 šlok + 2 šlo + 2 Dobre

Kreslenie spoločného faktora a objednávanie podmienok:

A = 2 šcele (a⋅b + b⋅c + c⋅a)

Zväzok

Ak sa ortoedro považuje za hranol, jeho objem sa vypočíta takto:

Objem = základná oblasť hranolu x Výška hranolu

V tomto prípade sa podlaha rozmerov považuje za obdĺžnikový c a do, Takže základná oblasť je Cleka.

Výška je daná dĺžkou b Od ortogonálnych okrajov po strany do a c.

Vynásobenie základnej oblasti (Ark) výškou b Máte objem Vložka Z Orthoedro:

V = a⋅b⋅c

Vnútorný

V ortoedro sú dva druhy diagonálov: vonkajšie diagonály a vnútorné diagonály.

Vonkajšie diagonály sú na obdĺžnikových tvári, zatiaľ čo vnútorné diagonály sú segmenty, ktoré sa spájajú s dvoma opačnými vrcholmi, ktoré sú chápané opačnými vrcholmi tých, ktoré nezdieľajú žiadne hrany.

V ortoedro sú štyri vnútorné uhlopriečky, všetky rovnaké miery. Dĺžka vnútorných diagonálov je možné získať z nanášania vety Pythagoras na obdĺžniky.

Môže vám slúžiť: trigonometrické funkcie: Základné, v karteziánskej rovine, príklady, cvičenie

Dĺžka D vonkajšieho diagonálu ortoedro podlahy spĺňa pythagorský vzťah:

d² = a² + c²

Podobne aj meranie vnútorného merania Pythagorského vzťahu:

D² = d² + b².

Kombinácia dvoch predchádzajúcich výrazov, ktoré máte:

D² = a² + c² + b².

Nakoniec je dĺžka ktorejkoľvek z vnútorných diagonálov Orthoedro daná nasledujúcim vzorcom:

D = √ (a² + b² + c² ). 

Príklady

- Príklad 1

Mason stavia nádrž na ortoedro, ktorého vnútorné rozmery sú: 6 m x 4 m a 2 m vysoká. Požaduje sa:

a) Určite vnútorný povrch nádrže, ak je v hornej časti úplne otvorený. 

b) Vypočítajte objem vnútorného priestoru nádrže.

c) Nájdite dĺžku vnútornej uhlopriečky.

d) Aká je kapacita nádrže v litroch?

Roztok

Berieme rozmery obdĺžnikovej bázy a = 4 ma c = 6 ma výška ako b = 2 m

Oblasť ortoedra s danými rozmermi je daná nasledujúcim vzťahom:

A = 2 šcele (a⋅b + b⋅c + c⋅a) = 2 šcele (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

To znamená:

A = 2 šcele (8 m² + 12 m² + 24 m²) = 2 šcela (44 m²) = 88 m²

Predchádzajúci výsledok je oblasť ortoedro uzavretého s danými rozmermi, ale keďže je to nádrž úplne objavená v hornej časti, aby sa získal povrch vnútorných stien nádrže, plocha chýbajúceho veka to je:

C⋅a = 6 m ⋅ 4 m = 24 m².

Nakoniec bude vnútorný povrch nádrže: s = 88 m² - 24 m² = 64 m².

Riešenie B

Vnútorný objem nádrže je daný objemom ortoedro vnútorných rozmerov nádrže:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Riešenie c

Interiérový diagonál oktadronu s rozmermi vnútra nádrže má dĺžku danú podľa:

Môže vám slúžiť: Kontinuálna náhodná premenná

√ (a² + b² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Vykonanie uvedených operácií, ktoré máme:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Riešenie d

Na výpočet kapacity nádrže v litroch je potrebné vedieť, že objem kubického decimera je rovnocenný s kapacitou litra. Predtým sa vypočítal objem v kubických metroch, ale musí sa transformovať na kubické decimetre a potom do litrov:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Cvičenie 2

Sklenené akvárium má kubický tvar 25 cm strany. Určiť oblasť v M², Objem v litroch a dĺžka vnútorného diagonálneho v CM.

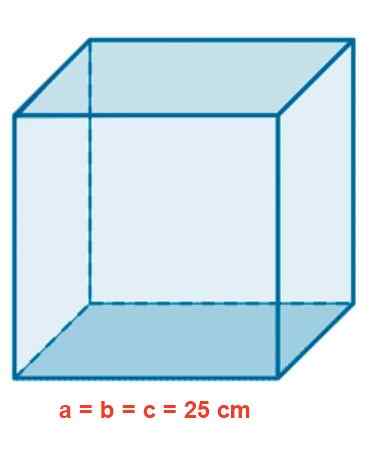Obrázok 4. Akvárium kubického skla.

Riešenie

Táto oblasť je vypočítaná rovnakým vzorcom Orthoedro, ale berúc do úvahy, že všetky rozmery sú totožné:

A = 2 šcenčine (3 a⋅a) = 6lek a² = 6 šcele (25 cm)² = 1.250 cm²

Objem kocky je daný:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15 625 dm³ = 15 625 l.

Dĺžka D vnútorného uhlopriečky je:

D = √ (3²) = 25√ (3) cm = 43,30 cm.

Odkazy

1. Arias j. Geogebra: Prism. Obnovené z: YouTube.com.
2. Kalkulácia.Dc. Cvičenia a problémy vyriešené v oblastiach a objemoch. Obnovené z: výpočtu.Dc.
3. Salvador R. Pyramída + ortoedro s geogebra (IHM). Obnovené z: YouTube.com
4. Weisstein, Eric. „Ortoedro“. Matematický svet. Výskum Wolfram.
5. Wikipedia. Ortoedro. Obnovené z: je.Wikipedia.com