Notácie vyvinuli, čo je, príklady a cvičenia
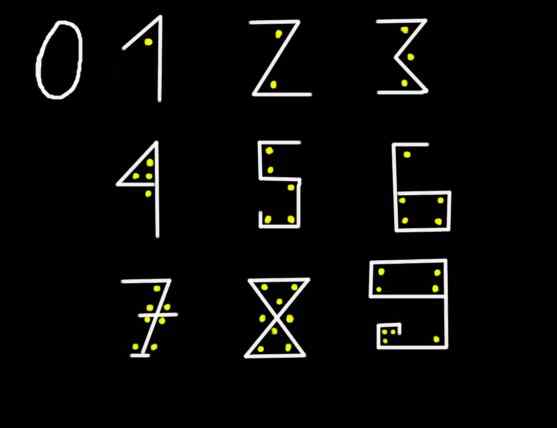
- 2517
- 109
- JUDr. Rudolf Čapkovič
Ten rozvinutý zápis Je to ten, v ktorom je číselný obrázok vyjadrený ako súčet, v ktorej sa zohľadňuje pozičná hodnota každej číslice, ktorá tvorí číslo.
Napríklad pri písaní čísla ako 2345 má každá číslica pozičnú hierarchiu. Čítanie pravej extrémnej číslice vľavo, hierarchia alebo hodnota rastie.
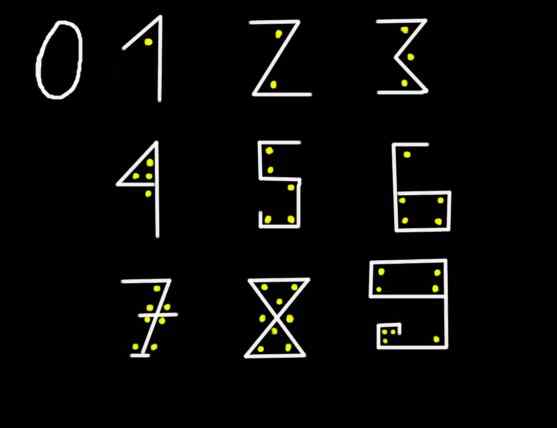 postava 1. Pri deviatich grafoch je možné reprezentovať ľubovoľný obrázok.
postava 1. Pri deviatich grafoch je možné reprezentovať ľubovoľný obrázok. Na obrázku 2345, číslica 5 predstavuje päť jednotiek, číslica 4 predstavuje štyri desiatky, 3 zodpovedá tretej pozícii zľava doprava, a preto 3 predstavuje tristo stovky, nakoniec 2 predstavujú dvetisíce dvetisíce. To znamená, že je v rozvinutom alebo rozšírenom zápise obrázok 2345 napísaný takto:
2345 = 2 tisíce + 3 sto + 4 desiatky + 5 jednotiek
Ale dá sa tiež vyjadriť takto:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Obrázok 2345 možno tiež napísať ako súčet právomocí 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Kde obicflejo ^ znamená zvýšenie uvedeného exponentu. Napríklad 10^3 = 10 x 10 x 10 = 1000. Ďalším spôsobom písania exponentov je dohľad:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
Systém na číslovanie
Systém arabských čísel sú čísla, ktoré sa používajú denne na drvivej väčšine kontinentov a krajín sveta. Arabské čísla sú základným systémom 10, pretože desať symbolov alebo grafónov sa používa na písanie ľubovoľného čísla. Týchto desať symbolov je:
0 1 2 3 4 5 6 7 8 9
Iba s jedným z týchto symbolov je možné vyjadriť obrázky medzi nulou do deväť. Na vyjadrenie čísel väčších ako deväť, pozičný systém založený na desiatich. Obrázok 10 je tucet a nulové jednotky. Obrázok 11 je tucet a jednotka. Obrázok 123 (sto dvadsať tri) je sto, dva desiatky a tri jednotky. Napísané vo forme právomocí desiatich čísla 123 bude:
Môže vám slúžiť: 60 deliteľov1 × 10^2 + 2 × 10^1 + 3 × 10^0
Kde:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
S týmto príkladom je zrejmé, že poloha číslice na konci je poloha 0 a predstavuje počet jednotiek, z druhej číslice sprava doľava je poloha 1 a predstavuje počet desiatok, tretí číslica (vpravo do ľavá) má polohu 2 a predstavuje stovky.
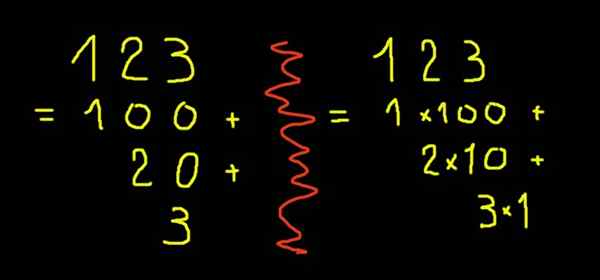 Obrázok 2. Vyvinutý zápis na obrázku 123.
Obrázok 2. Vyvinutý zápis na obrázku 123. Frakčné alebo desatinné čísla
S desatinným polohovým systémom je tiež možné.
Zastupovať frakciu ½ v arabskom desatinnom systéme, to znamená, že polovica jednotky je napísaná:
½ = 0,5
Na dosiahnutie tohto výrazu v našom systéme na základe 10 boli vykonané tieto operácie:
1- Vynásobte čitateľ a menovateľ na 5, aby ste mali ekvivalentnú frakciu 5/10 = 1/2.
2- Rozdelenie 10 je ekvivalentné vynásobeniu napájaním založeným na desiatich s exponentom menšími (10^-1), to je 5/10 = 5 × 10^-1.
3- Záporný exponent označuje, koľkokrát je číslica uvedená z polohy jednotky spustená alebo umiestnená, v našom prípade by to bolo 0,5.
4- ½ = 0,5 v rozšírenom zápise je napísané takto:
0,5 = 0x10^0 + 5 × 10^-1
Kde 10^-1 = 0,1 je desatina (frakcia zodpovedajúca jednotke rozdelenej do 10 rovnakých častí).
Týmto spôsobom číslo 0,5 zodpovedá piatim desatinám, ale číslo 0,05 zodpovedá 5 stotinám a 0,005 až 5 tisícin.
Môže vám slúžiť: Prečo je algebra dôležitá v určitých každodenných situáciách?Vyvinuté príklady notácie
Príklad 1
Vzhľadom na obrázok 40201 v štandardnom zápise ho prevod na vyvinutý zápis.
Riešenie:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Príklad 2
Napíšte frakciu ¾ v predĺženom zápise.
Riešenie:
V takom prípade existujú tri štvrtiny jednotky.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Povedal slovami, že by to bolo také:
Frakcia ¾ zodpovedá siedmim desiatkom plus päťstotiny.
Rozvinuté zápisové cvičenia
Cvičenie 1
Slovami povedzme výraz vyvinutý z obrázku 1 40201 v príklade 1.
Riešenie:
Rozvinutý zápis je taký:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Že v slovnom jazyku sa hovorí:
Štyri desiatky tisíc plus tisíc tisíc plus dvesto, viac nulových desiatok plus jednotka.
Cvičenie 2
Vyjadriť slovami predchádzajúci obrázok a rozložte vyvinutú zodpovedajúcu frázu.
Riešenie:
Obrázok 40201 slovami je vyjadrený takto:
Štyridsaťtisíc dvesto jeden
Predchádzajúca fráza sa môže vyvinúť ako:
40 × 1000 + 2 × 100 + 1
Dá sa povedať, že spôsob, ako vysloviť čísla, je polovičný spôsob, ako ich vyjadriť.
Cvičenie 3
Napíšte číslo 7/3 rozvinutého spôsobu.
Riešenie:
Je to obrázok vyjadrený ako nesprávna frakcia, pretože ako čitateľ je väčší ako menovateľ, číslo je väčšie ako jednotka.
Táto nesprávna frakcia sa dá rozdeliť ako súčet frakcií 6/3 + 1/3. Prvý z frakcií má za následok celé číslo 2, zatiaľ čo 1/3 = 0,333333, kde sa číslica 3 opakuje neurčito. Takže desatinná expresia vyvinutá z čísla 7/3 bude vždy približným výrazom:
Môže vám slúžiť: štvornásobné: prvky, vlastnosti, klasifikácia, príklady7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Cvičenie 6
Napíšte v štandardnom zápise a potom vyvinul číslo: Dvadsať tri miliardy dvesto päťdesiat miliónov päťsto stoviek dvadsať -šesťdesiat tisíc tristo dvadsať -Five s tromi dvadsiatimi tromi tisícinami.
Riešenie:
Je potrebné si uvedomiť, že a Millardo je ekvivalent jednej miliardy. Slovo Millardo Kráľovská Španielska akadémia ju prijala v roku 1995 na žiadosť neskoro venezuelského prezidenta Rafaela Caldera, člena venezuelskej akadémie jazyka. V takom prípade je číslo štandardného zápisu napísané takto:
23.2501526.325,023
23 miliárd + 250 miliónov + 526 tisíc + 325 jednotiek + 23 tisícin.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Nakoniec je napísaná postava v rozvinutej notácii:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Odkazy
- Khanská akadémia. Polohová hodnota tabuľky. Obnovené z: je.Khanacademy.orgán
- Khanská akadémia. Napíšte vyvinuté číslo (video). Obnovené z: je.Khanacademy.orgán
- Ifrah, Geoges (1998): Universal History of Figures. Espasa calpe s.Do.
- Wikipedia. Pozičný zápis. Obnovené z: je.Wikipedia.com
- Wikipedia. Millardo. Obnovené z: je.Wikipedia.com
- « Štruktúra oxidu fosforu (V), vlastnosti, získanie, použitie, riziká
- Štruktúra hliníka fosforečnanu (ALPO4), vlastnosti, získanie, použitie, použitie »

