Vlastnosti zložitých čísel, príklady, operácie

Ten zložité čísla Sú to numerická sada, ktorá pokrýva skutočné čísla a všetky korene polynómov, vrátane rovnomerných koreňov záporných čísel. Tieto korene neexistujú v súbore reálnych čísel, ale v zložitých číslach je riešenie.

Komplexné číslo pozostáva zo skutočnej časti a ďalšieho nazývaného „imaginárne“. Skutočná časť sa volá do, Napríklad imaginárna časť Ib, s do a b skutočné čísla a „ja“ ako Imaginárna jednotka. Týmto spôsobom má zložité číslo formulár:

Z = a + ib

postava 1.- Binomické znázornenie komplexného čísla z hľadiska skutočnej časti a imaginárnej časti. Zdroj: Pixabay.

Príklady komplexných čísel sú 2 - 3i, -πi, 1 + (1/2) i. Ale predtým, ako s nimi pracujem, pozrime sa, odkiaľ pochádza imaginárna jednotka Jo, Vzhľadom na túto kvadratickú rovnicu:

X² - 10x + 34 = 0

V ktorom a = 1, b = -10 a c = 34.

Keď sa na určenie riešenia použije vzorec rozpúšťadla, nájdeme nasledujúce:

Ako určiť hodnotu √-36? Neexistuje žiadne skutočné číslo, ktoré Square je záporná suma. Potom sa dospelo k záveru, že táto rovnica nemá skutočné riešenia.

Môžeme však napísať toto:

√-36 = √-6² = √6² (-1) = 6√-1

Ak definujeme určitú hodnotu X také:

X² = -1

Tak:

x = ± √-1

A predchádzajúca rovnica by mala riešenie. Preto bola imaginárna jednotka definovaná ako:

I = √-1

A tak:

√-36 = 6i

Mnoho matematikov staroveku pracovalo na riešení podobných problémov, zdôraznili renesančný Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) a Raffaele Bombelli (1526-1572).

O niekoľko rokov neskôr René Descartes (1596-1650) nazývaný „imaginárny“ do množstiev, ako napríklad √-36 príkladu. Z tohto dôvodu je √-1 známy ako Imaginárna jednotka.

[TOC]

Zložité čísla Vlastnosti

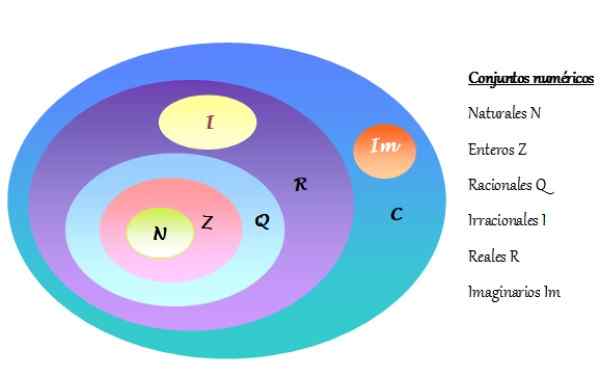
-Sada zložitých čísel je označená ako C a obsahuje reálne čísla r a imaginárne čísla im. Numerické súpravy sú znázornené na Vennovom diagrame, ako je to znázornené na nasledujúcom obrázku:

Môže vám slúžiť: Vyriešené faktorizačné cvičenia Obrázok 2. Venn Diagram numerických súprav. Zdroj: f. Zapata.

-Každé komplexné číslo pozostáva z jednej skutočnej časti a druhej imaginárnej časti.

-Ak je imaginárna časť komplexného čísla 0, je to čisté skutočné číslo.

-Ak je skutočná časť komplexného čísla 0, potom je číslo čisté imaginárne.

-Dve zložité čísla sú rovnaké, ak sú ich skutočná časť a imaginárna časť rovnaká.

-S komplexnými číslami sa vykonávajú známe operácie sumov, odčítania, násobenia, produktu a posilnenia, čo vedie k ďalšiemu komplexnému číslu.

Zastúpenie zložitých čísel

Zložité čísla môžu byť reprezentované rôznymi spôsobmi. Tu sú tie hlavné:

- Binomická forma

Je to danú formu na začiatku, kde z je komplexné číslo, do je skutočná časť, b je imaginárna časť a Jo Je to imaginárna jednotka:

Z = a + ib

Alebo tiež:

Z = x + iy

Jedným zo spôsobov grafu Komplexné číslo je cez komplexnú rovinu zobrazenú na tomto obrázku. Imaginárna os je zvislá, zatiaľ čo skutočná os je vodorovná a označuje ako re.

Komplexné číslo z Je zastúpený v tejto rovine ako súradnicový bod (X, y) ani (A, b), ako sa to robí s bodmi skutočnej roviny.

Vzdialenosť od pôvodu do bodu Z je modul komplexného čísla, označený ako r, zatiaľ čo φ je uhol, ktorý sa tvorí r So skutočnou osou.

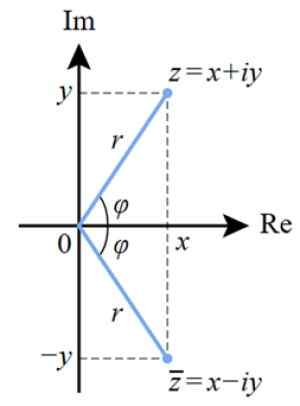Obrázok 3. Zastúpenie komplexného čísla v komplexnej rovine. Zdroj: Wikimedia Commons.

Toto zastúpenie úzko súvisí s reprezentáciou vektorov v skutočnej rovine. Hodnota R zodpovedá modul komplexného čísla.

Môže vám slúžiť: Metóda Gauss-Seidel: Vysvetlenie, aplikácie, príklady

- Polárna forma

Polárna forma spočíva v vyjadrení komplexného čísla, ktoré dáva hodnoty r a φ. Ak sa pozrieme na obrázok, hodnota r Zodpovedá hypotenusu pravého trojuholníka. Kategórie sa oplatia do a b, O dobre X a a.

V binomickej alebo binomickej forme môžeme prejsť na polárnu formu:

R = √x²+a²

Uhol φ Je to ten, ktorý tvorí segment R s horizontálnou osou alebo imaginárnou osou. Je to známe ako argument komplexného čísla. Tadiaľto:

φ = arctg (y/x)

Tento argument má nekonečné hodnoty, berúc do úvahy, že zakaždým, keď sa otočí návrat, čo má hodnotu 2π Radianes, R opäť zaberá rovnakú pozíciu. Týmto spôsobom je všeobecne argument Z, označený arg (z) vyjadrený takto:

Arg (z) = φ + 2kπ

Kde k je celé a slúži na označenie množstva zákrut otočených: 2, 3, 4 .. . Znak označuje význam rotácie, ak sa vytvorí čas alebo antihorario.

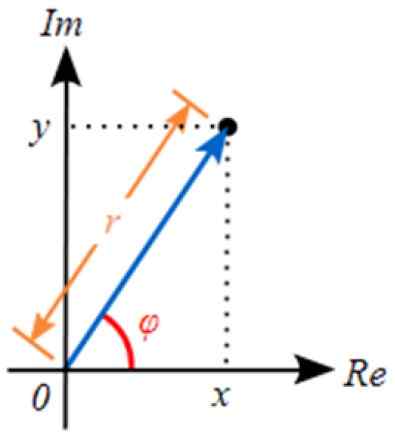Obrázok 4. Polárne znázornenie komplexného čísla v komplexnej rovine. Zdroj: Wikimedia Commons.

A ak chceme odovzdať polárnu formu do binomickej formy, používame trigonometrické dôvody. Z predchádzajúceho čísla vidíme, že:

x = r cos φ

y = r sen φ

Týmto spôsobom z = r (cos φ+i sin φ)

To je takto skrátene:

z = r cis φ

Príklady zložitých čísel

Binomálne sú uvedené nasledujúce komplexné čísla:

a) 3 + i

b) 4

d) -6i

A tieto v usporiadanom krútiacom momente:

a) (-5, -3)

b) (0, 9)

c) (7,0)

Nakoniec sa tejto skupine dostane polárne alebo trigonometrické:

a) √2 cis 45 °

b) √3 cis 30 °

Môže vám slúžiť: Hypergeometrické rozdelenie: vzorce, rovnice, model

c) 2 cis 315 °

Na čo sú?

Užitočnosť zložitých čísel presahuje rozlíšenie rovnice druhého stupňa uvedeného na začiatku, pretože sú nevyhnutné v oblasti inžinierstva a fyziky, najmä v:

-Štúdium elektromagnetických vĺn

-Analýza alternatívneho prúdu a napätia

-Modelovanie všetkých druhov signálov

-Teória relativity, kde sa čas považuje za imaginárnu veľkosť.

Operácie s komplexnými číslami

S komplexnými číslami môžeme vykonávať všetky operácie, ktoré sa vykonávajú so skutočnými. Niektoré sa dajú ľahšie urobiť, ak čísla prichádzajú binomicky, napríklad súčet a odčítanie. Na druhej strane, násobenie a rozdelenie sú jednoduchšie, ak sa vykonávajú s polárnou formou.

Pozrime sa na niekoľko príkladov:

- Príklad 1

Pridať z₁ = 2 + 5i a z₂ = -3 -8i

Riešenie

Skutočné časti sa pridávajú oddelene od imaginárnych častí:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Príklad 2

Vynásobiť z₁ = 4 cis 45 ° a z₂ = 5 cis 120 °

Riešenie

Dá sa preukázať, že produkt dvoch zložitých čísel v polárnych alebo trigonometriách je daný:

z₁ . z₂ = r₁.r₂ Cis (φ₁ + φ₂)

Na základe tohto:

z₁ . z₂ = (4 × 5) CIS (45 + 120) = 20 cis 165 °

Aplikácia

Jednoduchá aplikácia komplexných čísel je nájsť všetky korene polynomiálnej rovnice, ako je napríklad tá, ktorá je uvedená na začiatku článku.

V prípade rovnice x² - 10x + 34 = 0, pri aplikácii vzorec rozpúšťadla, ktorý sa získa:

Preto sú riešenia:

X₁ = 5 + 3i

X₂ = 5 - 3i

Odkazy

1. Gróf, r. Zložité čísla. Získané z: matematiky.vôl.Ac.Uk.
2. Figuera, J. 2000. Matematika 1. Diverzifikovaný. Edície Co-Bo.
3. Hoffmann, J. 2005. Výber matematických problémov. Publikácie Monfort.
4. Jiménez, r. 2008. Algebra. Sála.
5. Wikipedia. Zložité čísla. Zdroj: In.Wikipedia.orgán