Charakteristické prvotné čísla, príklady, cvičenia

Ten základné čísla, tiež nazývané absolútni bratranci, sú tie prirodzené čísla, ktoré sú navzájom deliteľné a 1. V tejto kategórii čísla ako: 2, 3, 5, 7, 11, 13, 17, 19, 23 a mnoho ďalších prichádza v tejto kategórii.

Na druhej strane je zložené číslo samy o sebe deliteľné, o 1 a aspoň jedno ďalšie číslo. Máme napríklad 12, čo je deliteľné 1, 2, 4, 6 a 12. Na základe dohovoru 1 nie je zahrnutý v zozname prvých čísel alebo v zlúčeninách.

postava 1. Niektoré prvotné čísla. Zdroj: Wikimedia Commons.

Znalosť prvých čísel pochádza zo vzdialených časov; Starí Egypťania ich už zaobchádzali a boli určite známi už dávno predtým.

Tieto čísla sú veľmi dôležité, pretože akékoľvek prirodzené číslo môže byť reprezentované produktom prvých čísel, čo je táto jedinečná reprezentácia, s výnimkou poradia faktorov.

Táto skutočnosť je úplne zavedená v vete zvanej Základná veta aritmetiky, čo uvádza, že čísla, ktoré nie sú bratrancami.

[TOC]

Charakteristiky prvých čísel

Pod hlavnými charakteristikami prvých čísel:

-Sú nekonečné, pretože akokoľvek veľké číslo je možné nájsť vždy.

-Ak je hlavné číslo p sa presne nerozdeľuje na iné číslo do, Potom sa hovorí p a do Sú to bratranci navzájom. Keď sa to stane, jediný spoločný deliteľ je obaja 1.

Nie je potrebné do Byť absolútnym bratranec. Napríklad 5 je bratranec, a hoci 12 nie je, obidve čísla sú navzájom bratranci, pretože títo dvaja majú spoločný deliteľ na 1.

-Keď je hlavné číslo p Rozdeľte silu čísla n, Tiež rozdeľuje a n. Zvážte 100, čo je sila 10, konkrétne 10². Stáva sa, že 2 rozdeľujú 100 a 10.

-Všetky prvotné čísla sú nepárne s výnimkou 2, preto ich posledná číslica je 1, 3, 7 alebo 9. 5 nie je zahrnutá, pretože hoci je to čudné a bratranec, nikdy nie je konečnou postavou iného prvočísla. V skutočnosti všetky čísla, ktoré končia v 5, sú násobky, a preto nie sú bratrancami.

Môže vám slúžiť: Centrálna symetria: Vlastnosti, príklady a cvičenia

-Jo p Je to bratranec a deliteľ produktu dvoch čísel do.b, tak p Rozdeľte jednu z nich. Napríklad hlavné číslo 3 rozdeľuje produkt 9 x 11 = 99, pretože 3 je deliteľ 9.

Ako zistiť, či je číslo bratranec

Ten Prvoradosť Je to názov daný kvalite bratranca. Francúzsky matematický Fermatova malá veta, To hovorí:

„Vzhľadom na prirodzené číslo bratranca p a akékoľvek prirodzené číslo do viac ako 0, je to splnené do^p - do Je to násobok p, tak dlho p byť bratranec “.

Môžeme to potvrdiť napríklad pomocou malých čísel, napríklad predpokladajme P = 4, že už vieme, že to nie je bratranec a A = 6:

6⁴ - 6 = 1296 - 6 = 1290

Číslo 1290 nie je presne deliteľné medzi 4, preto 4 nie je hlavným číslom.

Urobme teraz test s p = 5, ktorým je bratranec a A = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 je deliteľné medzi 5, pretože akékoľvek číslo, ktoré končí na 0 alebo 5, je. V skutočnosti 7760/5 = 1554. Keď je splnená malá veta Fermata, môžeme zabezpečiť, aby 5 bolo hlavným číslom.

Test cez vetu je efektívny a priamy s malými číslami, v ktorých sa operácia ľahko vykonáva, ale čo robiť, ak nás požiadajú, aby sme zistili pôvodnosť veľkého počtu?

V takom prípade je číslo postupne rozdelené medzi všetky menšie čísla, až do určitého presného rozdelenia alebo že kvocient je menší ako deliteľ.

Ak je akékoľvek rozdelenie presné, znamená to, že číslo je zložené a ak je kvocient menší ako deliteľ, znamená to, že číslo je bratranec. V tomto roku to uvedieme do praxe vyriešené 2.

Spôsoby, ako nájsť prvotné číslo

Existujú nekonečné čísla a neexistuje žiadny jedinečný vzorec na ich určenie. Pozorovanie niektorých prvých čísel, ako sú tieto:

Môže vám slúžiť: Nulový uhol: Definícia a charakteristiky, príklady, cvičenia

3, 7, 31, 127 ..

Zistilo sa, že sú vo forme 2ⁿ - 1, s n = 2, 3, 5, 7, 9 ... uisťujeme vás:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Ale nemôžeme ubezpečiť, že vo všeobecnosti 2ⁿ - 1 buď bratrancom, pretože existujú určité hodnoty n pre ktoré to nefunguje, napríklad na 4:

2⁴ - 1 = 16 - 1 = 15

A číslo 15 nie je bratranec, pretože končí 5. Jedno z najväčších hlavných čísel, ktoré sú známe, nachádzajúce sa pomocou výpočtov vytvorených počítačom, je však vo formulári 2ⁿ - 1 s:

N = 57.885.161

Ten Mersenne Formula uisťuje nás, že 2^p - 1 je vždy bratranec, pokiaľ p Buďte tiež bratrancom. Napríklad 31 je bratranec, takže je isté, že 2³¹ - 1 Je to tiež:

2³¹ - 1 = 2.147.483.647

Vzorec však umožňuje určiť iba niektoré prvotné čísla, nie všetky.

Eulerov vzorec

Nasledujúci polynóm umožňuje nájsť prvotné čísla, pokiaľ N je medzi 0 a 39:

P (n) = n² + N + 41

Neskôr v sekcii vyriešených cvičení je príklad jeho použitia.

Skríning eratosténov

Eratóstenes bol postavou a matematickým starovekým Gréckom, ktorý žil v treťom storočí.C. Navrhol grafickú metódu hľadania prvých čísel, ktoré môžeme uviesť do praxe s malými číslami, nazýva sa obrazovka Eratóstenes (obrazovka je ako sitko).

-Čísla sú umiestnené v tabuľke, ako je ten, ktorý je uvedený v animácii.

-Potom sú párne čísla označené, s výnimkou 2, o ktorých vieme, že je bratranec. Všetci ostatní sú to násobky, a preto nie sú bratrancami.

-Násobky 3, 5, 7 a 11 sú tiež označené, s výnimkou všetkých, pretože vieme, že sú to bratranci.

-Násobky 4, 6, 8, 9 a 10 sú už označené, pretože ide o zlúčeniny, a preto násobky niektorého z označených bratrancov.

Môže vám slúžiť: História trigonometrie z jej pôvodu

-Nakoniec, zostávajúce čísla sú neoznačené, sú bratranci.

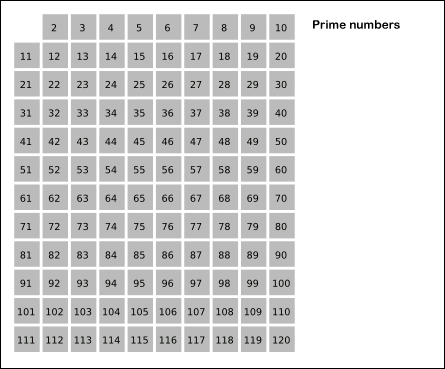Obrázok 2. Eratosténny premietacia animácia. Zdroj: Wikimedia Commons.

Cvičenia

- Cvičenie 1

Pomocou polynómu Eulera pre primárne čísla nájdite 3 čísla väčšie ako 100.

Riešenie

Toto je polynóm, ktorý Euler navrhol nájsť primárne čísla, ktoré fungujú pre hodnoty n medzi 0 a 39.

P (n) = n² + N + 41

Prostredníctvom Tanteo vyberieme hodnotu n, napríklad n = 8:

P (8) = 8² + 8 + 41 = 113

Pretože n = 8 vytvára prvotné číslo väčšie ako 100, potom vyhodnotíme polynóm pre n = 9 a n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Cvičenie 2

Zistite, či sú nasledujúce čísla bratranci:

a) 13

b) 191

Roztok

13 je dostatočne malý na to, aby použil Fermatovu malú vetu a pomoc kalkulačky.

Používame a = 2, aby čísla neboli príliš veľké, hoci ich môžu použiť aj a = 3, 4 alebo 5:

2¹³ - 2 = 8190

8190 je deliteľný medzi 2, pretože je dokonca, preto 13 je bratranec. Čitateľ ho môže potvrdiť tým, že urobí rovnaký test s a = 3.

Riešenie B

191 je veľmi veľký na vyskúšanie vety a spoločnej kalkulačky, ale môžeme rozdeliť rozdelenie medzi každým hlavným číslom. Vynecháme rozdelenie 2, pretože 191 nie je ani a rozdelenie nebude presné alebo pomer menší ako 2.

Pokúsili sme sa rozdeliť o 3:

191/3 = 63 666…

A nedáva presný, ani kvocient nie je menší ako deliteľ (63 666 ... je väčší ako 3)

Pokračujeme v teste 191 bratrancami 5, 7, 11, 13 a presné rozdelenie sa nedosiahne, ani pomer menší ako deliteľ. Kým sa nerozdelí medzi 17:

191/17 = 11, 2352 ..

Pretože to nie je presné a 11 2352 ... je to menej ako 17, číslo 191 je bratranec.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Prieto, C. Primo. Zdroj: stránky.Matem.Žobrák.mx.
3. Vlastnosti prvých čísel. Získané z: mae.Ufl.Edu.
4. Šikovný. Primo čísla: Ako ich nájsť so sitom Eratosténov. Získané z: Smartick.je.
5. Wikipedia. prvočíslo. Obnovené z: je.Wikipedia.orgán.