Tachtenbergova metóda Čo je, príklady

On Trachtenberg Je to systém na vykonávanie aritmetických operácií, hlavne násobenie, ľahké a rýchle, akonáhle sú ich pravidlá známe a dominujú.

Bol navrhnutý ruským inžinierom Jakowom Trachtenbergom (1888-1953), keď bol väzňom nacistov v koncentračnom tábore, ako forma rozptyľovania na udržanie zdravého rozumu, zatiaľ čo pokračoval v zajatí.

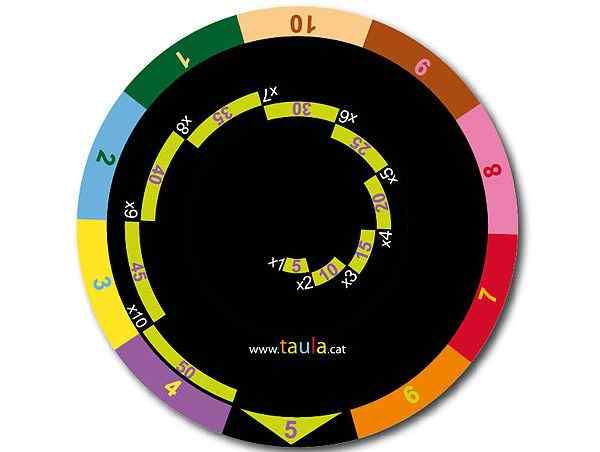
postava 1. Násobenie. Zdroj: Wikimedia Commons. Taulacat [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)] [TOC]

Čo sú výhody a nevýhody

Výhodou, ktorú táto metóda predstavuje, je to, že na vykonanie multiplikácií nie je potrebné.

Nevýhodou je, že neexistuje univerzálne pravidlo, ktoré by sa množilo akýmkoľvek obrázkom, ale pravidlo sa líši podľa multiplikátora. Vzory sa však nie je ťažké si zapamätať a v zásade umožňujú operácie bez papiera a ceruzky.

V tomto článku sa sústredíme na pravidlá, aby sme sa rýchlo znásobili.

[TOC]

Príklady

Na uplatnenie metódy je potrebné poznať pravidlá, preto im predstavíme jeden po druhom a s príkladmi:

- Vynásobte obrázok 10 alebo 11

Násobenie pravidla o 10

-Na vynásobenie ľubovoľného obrázku 10 sa nula jednoducho pridá doprava. Napríklad: 52 x 10 = 520.

Pravidlá na vynásobenie 11

-Na začiatok a na konci obrázku sa pridá nula.

-Každá číslica sa pridá s pravicovým susedom a výsledok je umiestnený pod príslušnú číslicu pôvodného obrázku.

-Ak výsledok presahuje deväť, potom je zaznamenaná jednotka a je kladený malý bod, aby sme si uvedomili, že nosíme jednotku, ktorá sa pridá do súčtu nasledujúceho čísla s jej pravicovým susedom.

Podrobný príklad násobenia o 11

Vynásobte 673179 o 11

Môže vám slúžiť: Konvergenčné rádio: Definícia, príklady a cvičenia vyriešené

06731790 x 11 =

--

= 7404969

Potrebné kroky na dosiahnutie tohto výsledku, znázornené farbami, sú nasledujúce:

-1 z multiplikačnej jednotky (11) sa vynásobil multiplikátor 9 (06731790) a bol pridaný 0. Získala sa jednotná číslica: 9.

-Potom sa vynásobí 1 x 7 a pridá deväť dáva 16 a máme 1, tucet číslic je umiestnených: 6.

-Potom sa vynásobte 1 x 1, pridaný susedom pravého 7 plus 1, ktorý viedol v dôsledku toho 9 Na sto.

-Ďalší obrázok sa získa z vynásobenia 1 x 3 plus susedné 1, výsledkom je 4 Pre číslicu tisícov.

-Sa vynásobí 1 x 7 a sused sa pridá, čo je výsledkom 10, nula sa umiestni (0) ako desiatka číslica a berie si jednu.

-Potom 1 pre 6 plus sused 7 je 13 plus 1, ktorý bol 14, 4 ako číslica stotisíc a trvá 1.

-Nakoniec vynásobte 1 nula, ktorá bola pridaná na začiatok. Je to konečne 7 Pre číslicu zodpovedajúcu miliónom.

- Násobenie číslami od 12 do 19

Vynásobenie 12 akejkoľvek obrázku: 

-Na začiatok sa pridá nula a ďalšia nula na konci obrázku, aby sa množila.

-Každá číslica sa zdvojnásobí z obrázku, ktorý sa má vynásobiť a pridáva sa so svojím pravým susedom.

-Ak súčet presiahne 10, jednotka sa pridá k ďalšej operácii duplikácie a pridá sa k susedovi.

Príklad násobenia 12

Vynásobte 63247 o 12

0632470 x 12 =

-

758964

Podrobnosti na dosiahnutie tohto výsledku, prísne dodržiavajúce pravidlá stanovené, sú uvedené na nasledujúcom obrázku:

Obrázok 2. Trachtenbergova metóda na vynásobenie ľubovoľného čísla 12. Zdroj: f. Zapata.

- Rozšírenie pravidiel pre násobenie o 13, ... do 19

Metóda množenia 12 sa môže rozšíriť na násobenie o 13, 14 do 19, ktorá jednoducho zmení pravidlo duplikácie v prípade trinástich, štvornásobne v prípade 14 a tak ďalej, až kým nedosiahne 19 rokov.

Môže vám slúžiť: Ortogonálna matica: Vlastnosti, demonštrácia, príklady

Pravidlá pre výrobky do 6, 7 a 5

- Násobenie o 6

-Pridajte nuly na začiatok a koniec obrázka, ktoré sa majú vynásobiť 6.

-Pridajte polovicu svojej pravice napravo ku každej číslici, ale ak je číslica nepárne na pridanie 5 navyše.

Obrázok 3. Násobenie obrázku 6, podľa metódy trachtenbergu. Zdroj: f. Zapata.

- Násobenie o 7

-Pridajte nuly na začiatok a na konci obrázku, aby ste sa množili.

-Duplikovať každú číslicu a pridajte dolnú celú polovicu suseda, ale ak je číslica navyše pridajte 5.

Príklad násobenia o 7

-Vynásobte 3412 o 7

-Výsledkom je 23884. Ak chcete uplatniť pravidlá, odporúča sa najprv rozpoznať nepárne číslice a umiestniť malú 5, aby ste si zapamätali pridanie tohto čísla k výsledku.

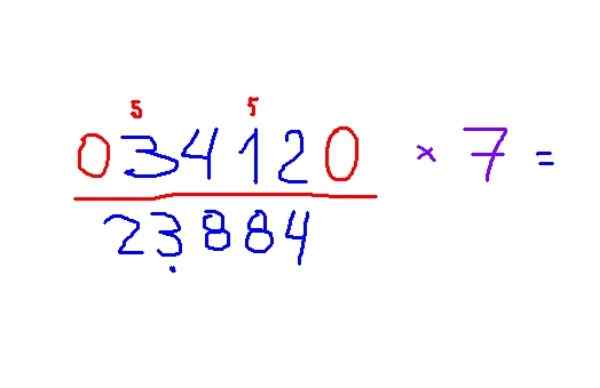Obrázok 4. Príklad násobenia obrázku 7 podľa Trachtenbergovej metódy. Zdroj: f. Zapata.

- Násobenie o 5

-Pridajte nuly na začiatok a na konci obrázku, aby ste sa množili.

-Umiestnite pod každú číslicu spodnú polovicu suseda napravo, ale ak je číslica navyše nepárne 5.

Príklad násobenia o 5

Vynásobte 256413 o 5

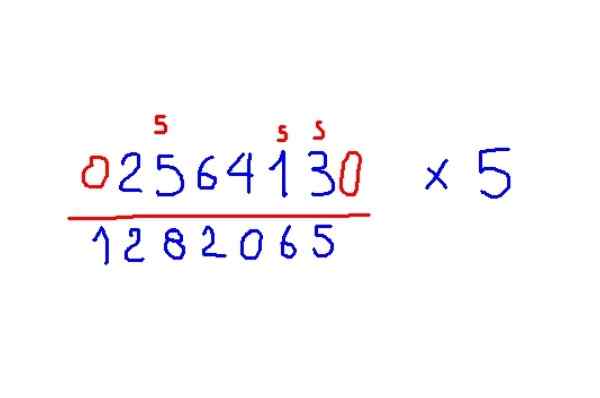Obrázok 5. Príklad násobenia obrázka 5 podľa metódy trachtenbergu. Zdroj: f. Zapata.

Pravidlá pre výrobky do 9

-Na začiatok sa pridá nula a ďalšia na konci obrázku, aby sa vynásobila deväť.

-Prvá číslica vpravo sa získa od odpočítania zodpovedajúcej číslice obrázku, aby sa vynásobila.

-Potom sa odpočíta ďalšia číslica a pridá sa sused.

-Predchádzajúci krok sa opakuje, až kým nedosiahnete nulu vynásobenia, kde odpočítame 1 od suseda a výsledok sa skopíruje pod nulu.

Môže vám slúžiť: aké sú delení z 30? (Vysvetlenie)

Príklad násobenia 9

Vynásobte 8769 x 9:

087690 x 9 =

--

78921

Operácie

10 - 9 = 1

(9-6) + 9 = 12 ( 2 A trvá to 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Násobenie 8, 4, 3 a 2

-Pridajte nuly na začiatok a na konci obrázku, aby ste sa množili.

-Pre prvú číslicu napravo odpočítajte od 10 a výsledok sa zdvojnásobí.

-Pre nasledujúce číslice odpočítajú od 9, výsledok sa zdvojnásobí a pridá sa sused.

-Po dosiahnutí nulového odpočítania 2 od pravej pravice.

- Násobenie o 8

Príklad násobenia 8

-Vynásobte 789 o 8

Obrázok 6. Príklad násobenia obrázka 8, podľa metódy trachtenbergu. Zdroj: f. Zapata.

- Násobenie 4

-Pridajte nuly doprava a doľava od znásobenia.

-Odpočítajte od 10 zodpovedajúcu číslicu jednotky Pridanie 5, ak je to zvláštna číslica.

-Odpočítajte od 9 vo forme každej vynásobenej číslice, pridajte polovicu suseda vpravo a ak je to zvláštna číslica na pridanie 5 navyše.

-Po dosiahnutí nuly na začiatku množeného miesta polovica suseda okrem jedného.

Príklad násobenia o 4

Vynásobte 365187 x 4

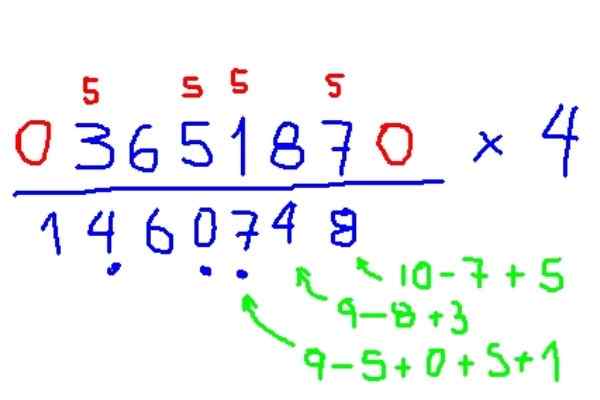Obrázok 7. Príklad násobenia obrázka 4, podľa metódy trachtenbergu. Zdroj: f. Zapata.

- Násobenie 3

-Pridajte nulu ku každému koncu násobenia.

-Odčítajte 10 s výnimkou číslice jednotky a pridajte 5, ak je to zvláštna číslica.

-Pokiaľ ide o ostatné číslice, odpočítajte 9 duplikujte výsledok, pridajte polovicu suseda a pridajte 5, ak je nepárny.

-Po dosiahnutí nuly hlavičky umiestnite celú polovicu suseda mínus 2.

Príklad násobenia 3

Vynásobte 2588 o 3

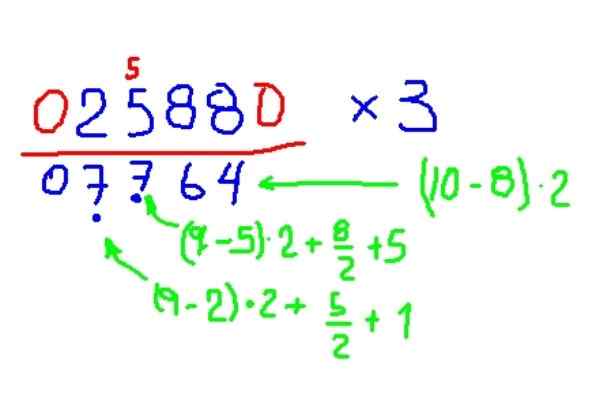Obrázok 8. Príklad násobenia obrázku 3, podľa metódy Trachtenbergu. Zdroj: f. Zapata.

- Násobenie 2

-Pridajte nuly na konce a zdvojnásobte každú číslicu, ak prekročíte 10, pridajte jednu do nasledujúceho.

Príklad násobenia o 2

Vynásobte 2374 o 2

023740 x 2

04748

Vynásobte kompozitnými číslami

Uplatňujú sa vyššie uvedené pravidlá, ale výsledky spúšťajú vľavo počet miest zodpovedajúcich desiatkam, stovkám atď. Pozrime sa na nasledujúci príklad:

Cvičenie 

Vynásobte 37654 498

0376540 x 498

301232 Pravidlo pre 8

338886 Pravidlo pre 9

150616 Pravidlo pre 4

18751692 Konečná suma

Odkazy

1. Cutler, Ann. 1960.Trachtenbergový systém rýchlosti základnej matematiky. Doubleday & Co, NY.
2. DialNet. Rýchly základný matematický systém. Obnovené z: DialNet.com
3. Matematický roh. Rýchle násobenie metódou trachtenbergu. Zotavené z: Rinconmatematical.com
4. Trachtenbergový systém rýchlosti základnej matematiky. Získané z: TrachtenbergSpeedMath.com
5. Wikipedia. Trachtenberg. Získané z: Wikipedia.com