Polohové opatrenia, centrálna tendencia a disperzia

Ten opatrenia strednej, disperznej a polohovej tendencie, Toto sú hodnoty použité na správne interpretáciu súboru štatistických údajov. Môžu sa prepracovať priamo, ako je získané zo štatistickej štúdie, alebo sa môžu organizovať v skupinách rovnakej frekvencie, čo uľahčuje analýzu.

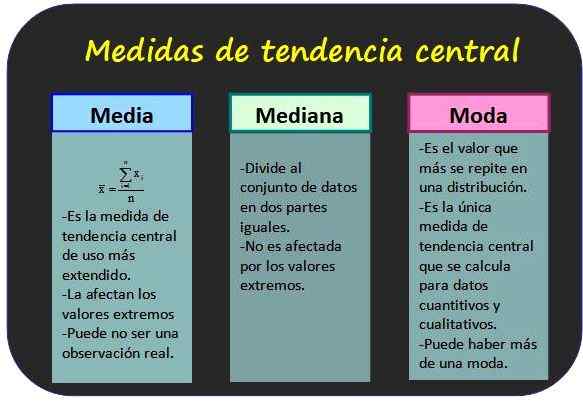
Tri najznámejšie ústredné trendy a niektoré z jeho vlastností. Zdroj: f. Zapata.

Opatrenia centrálnej tendencie

Umožňujú vedieť o tom, aké hodnoty sú štatistické údaje zoskupené dohromady.

Aritmetický priemer

Je tiež známy ako priemer hodnôt premennej a získa sa pridaním všetkých hodnôt a vydelením výsledku celkovým počtom údajov.

• Aritmetický priemer pre údaje bez zoskupenia

Byť premennou X, z ktorých neexistujú žiadne údaje bez organizácie alebo zoskupenia, jeho aritmetický priemer sa vypočíta takto:

A súhrnný zápis:

Príklad

Majitelia horského turistického hostela majú v úmysle vedieť, koľko dní v priemere zostáva v zariadeniach. Za týmto účelom sa uskutočnil záznam o dňoch stálosti 20 skupín turistov, čo získalo tieto údaje:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Priemerné dni, ktoré turisti zostávajú, sú:

= 2.5 dní

• Aritmetický priemer pre zoskupené údaje

Ak sú premenné údaje usporiadané v absolútnej frekvenčnej tabuľke f_Jo A triedne centrá sú x₁, X₂,…, X_n, Priemer sa počíta:

V súhrne leta:

Stredný

Medián skupiny n hodnoty premennej x je ústrednou hodnotou skupiny za predpokladu, že hodnoty sú čoraz viac usporiadané. Týmto spôsobom je polovica všetkých hodnôt nižšia ako móda a druhá polovica je väčšia.

• Médium neoskupených údajov

Môžu byť predložené nasledujúce prípady:

-Číslo n hodnoty premennej x  zvláštny: Medián je hodnota, ktorá je práve v strede skupiny hodnôt:

-Číslo n hodnoty premennej x spárovať: V tomto prípade sa medián vypočíta ako priemer dvoch centrálnych hodnôt dátovej skupiny:

Príklad

Ak chcete nájsť medián turistických údajov o ubytovni, sú najprv objednané od najmenej k najväčšiemu:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Môže vám slúžiť: Aká je relatívna frekvencia a ako sa vypočítava?

Číslo údajov je dokonca, preto existujú dva centrálne údaje: x₁₀ a x_jedenásť A keďže obidve majú hodnotu 2, jeho priemer je tiež.

Medián = 2

• Médium zoskupených údajov

Používa sa nasledujúci vzorec:

Symboly vo vzorci znamenajú:

-C: Šírka intervalu obsahujúceho medián

-B_M: nižšia hranica toho istého intervalu

-F_m: Počet pozorovaní obsahujúcich interval, ku ktorému medián patrí.

-N: Celkové údaje.

-F_BM: Počet pozorovaní pred intervalom obsahujúcim medián.

Formovať

Móda pre nedosiahnuté údaje je najfrekvenčnejšou hodnotou, zatiaľ čo pre zoskupené údaje je to najfrekvenčnejšia trieda. Považuje sa za módu za najreprezentatívnejšie údaje alebo triedu distribúcie.

Dve dôležité charakteristiky tohto opatrenia je to, že súbor údajov môže mať viac ako jednu módu a móda je možné určiť pre kvantitatívne údaje a kvalitatívne údaje.

Príklad

Pokračovanie v údajoch turistického hostela, ten, ktorý sa najviac opakuje, je 1, preto najbežnejšou vecou je, že turisti zostávajú 1 deň v hosteli.

Opatrenia

Disperzné opatrenia opisujú, ako sú zoskupené údaje okolo centrálnych opatrení.

Rozsah

Vypočíta sa odpočítaním hlavných údajov a menších údajov. Ak je tento rozdiel veľký, je to znamenie, že údaje sú rozptýlené, zatiaľ čo malé hodnoty naznačujú, že údaje sú blízko priemeru.

Príklad

Rozsah pre údaje o turistických hosteli je:

Rozsah = 5 - 1 = 4

Rozptyl

• Rozptyl pre údaje, ktoré nie sú skupinami

Nájsť rozptyl s² Je potrebné najprv poznať aritmetický priemer, potom sa rozdiel vypočíta na štvorec medzi každými údajmi a priemerom, všetky sú pridané a vydelené celkovými pozorovaniami. Tieto rozdiely sú známe ako odchýlka.

Rozptyl, ktorý je vždy kladný (alebo nula), naznačuje, ako ďaleko sú pozorovania priemeru: ak je rozptyl vysoký, hodnoty sú viac rozptýlené ako keď je rozptyl malý.

Príklad

Rozptyl údajov turistického hostela je:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Rozptyl pre zoskupené údaje

Na nájdenie rozptylu skupiny zoskupených údajov sú potrebné: i) priemer, ii) frekvencia f_Jo  čo sú celkové údaje v každej triede a iii) x_Jo  alebo hodnota triedy:

Môže vám slúžiť: typy trojuholníkov

Štandardná odchýlka

Štandardná odchýlka je pozitívnou druhou odmocninou rozptylu, takže má výhodu oproti rozptylu: prichádza v rovnakých jednotkách ako študovaná premenná, a preto má priamejšiu myšlienku ako blízko alebo ďaleko, čo je premenná priemeru.

• Štandardná odchýlka pre nepodpojené údaje

Určite sa jednoducho nájdením druhej odmocniny rozptylu pre nenaplnené údaje:

 Príklad

Štandardná odchýlka pre údaje o turistických hosteli je:

S = √ (s²) = √1.95 = 1.40

• Štandardná odchýlka pre zoskupené údaje

Vypočíta sa nájdením odmocniny rozptylu pre zoskupené údaje:

Poloha

Umiestnenie polohy rozdeľujú usporiadanú sadu údajov na rovnaké časti. Medián, okrem toho, že je ústrednou mierou tendencie, je tiež mierou polohy, pretože rozdeľuje celok na dve rovnaké časti. Ale môžete získať menšie diely s kvartilom, decilmi a percentilmi.

Kvartily

Kvartily rozdeľujú súpravu na štyri rovnaké časti, z ktorých každá má 25 % údajov. Sú označené ako q₁, Otázka₂ a Q₃ A medián je kvartilová q₂. Týmto spôsobom je 25% údajov pod kvartilom Q₁, 50% pod kvartilom q₂ alebo medián a 75% pod kvartilom q₃.

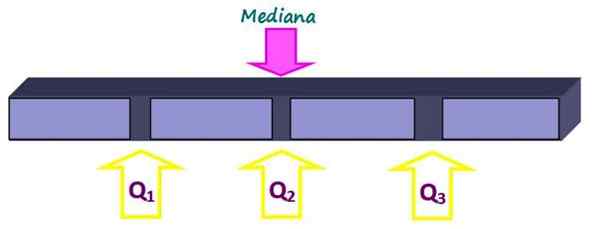Obrázok 2. Kvartily rozdeľujú súbor údajov na štyri rovnaké časti. Zdroj: f. Zapata.

• Kvartily pre nedospelé údaje

Údaje sa objednajú a celková suma je rozdelená do 4 skupín s rovnakým počtom údajov. Poloha prvého kvartilu sa nachádza:

Otázka₁ = (n+1)/4

Byť celkovým údajom. Ak výsledkom sú celé údaje zodpovedajúce tejto polohe, ale ak sú desatinné, údaje zodpovedajúce celej časti s nasledujúcim spôsobom sú spriemerované alebo pre väčšiu presnosť sa lineárne interpolujú medzi uvedenými údajmi.

Príklad

Poloha prvého kvartilu Q₁ Pre údaje z turistického hostela je:

Otázka₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Toto je poloha kvartilu 1 a ako výsledok je desatinná, hľadá sa dáta X Data₅ a x_6, ktoré sú x₅ = 1 a x₆ = 1 a sú spriemerované, čo je výsledkom:

Prvý kvartil = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Poloha druhého kvartilu Q₂ je:

Môže vám slúžiť: Teleskopický súčet: Ako je vyriešené a vyriešené cvičenia

Otázka₂ = 2 (n+1)/4 = 10.5

Čo je priemer medzi x₁₀ a x_jedenásť a zhoduje sa s mediánom:

Druhý kvartil = medián = 2

Tretia kvartilová poloha sa vypočíta podľa:

Otázka₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Je tiež desatinná, preto sa X spriemeruje_pätnásť a x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Ale ako obaja majú hodnotu 4:

Tretí kvartil = 4

Všeobecný vzorec pre polohu kvartilov v nenaplnených údajoch je:

Otázka_{klimatizovať} = K (n+1)/4

S k = 1,2,3.

• Kvartily pre zoskupené údaje

Vypočítajú sa podobne ako medián:

Vysvetlenie symbolov je:

-B_Otázka: Dolná hranica intervalu obsahujúceho kvartil

-C: Šírka tohto intervalu

-F_Otázka: Počet pozorovaní obsahovalo kvartilový interval.

-N: Celkové údaje.

-F_BQ: Počet údajov pred intervalom obsahujúcim kvartil.

Decil a percentily

Decily a percentily rozdeľujú súbory údajov na 10 rovnakých častí a 100 rovnakých častí a ich výpočet sa vykonáva analogický k kvartilom.

• Decils a percentily pre neprinoceničné údaje

Vzorce sa používajú: respektíve:

D_{klimatizovať} = K (n+1)/10

S k = 1,2,3… 9.

Decil d₅ Musí sa to rovnať mediánu.

P_{klimatizovať} = K (n+1)/100

S k = 1,2,3… 99.

Percentil P_päťdesiat Musí sa to rovnať mediánu.

Príklad

V príklade turistického hostela je pozícia D₃ je:

D₃ = 3 (20+1)/10 = 6.3

Ako je spriemerované desatinné číslo x₆ a x_7, Obidve sa rovnajú 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Znamená, že 3 desatiny údajov sú pod x₇ = 1 a zostávajúce vyššie.

• Decily a percentily pre zoskupené údaje

Vzorce sú analogické s kvartilom. D sa používa na označenie decil a p pre percentily a symboly sa interpretujú podobným spôsobom:

Empirické pravidlo

Ak sa údaje distribuujú symetricky a distribúcia je unimodálna, existuje pravidlo nazývané  Empirické pravidlo ani Pravidlo 68 - 95 - 99, že ich zoskupuje v nasledujúcich intervaloch:

• 68% údajov je v intervale:

• 95% údajov je v intervale:

• 99% údajov je v intervale:

Príklad

V akom intervale je 95% údajov z turistických hostelov?

Sú v intervale: [2.5-1.40; 2.5+1.40] = [1.1; 3.9].

Odkazy

1. Berenson, m. 1985. Štatistiky pre správu a ekonomiku. Inter -American S.Do.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.
4. Spiegel, m. 2009. Štatistika. Séria Schaum. 4 ta. Vydanie. McGraw Hill.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.