Vzorce koeficientov určovania, výpočet, interpretácia, príklady

On Určovací koeficient Je to číslo medzi 0 a 1, ktoré predstavuje zlomok bodov (x, y), ktoré sledujú riadok nastavenia regresiou súboru údajov s dvoma premennými.

Je tiež známy ako dobrota a je označený r². Na jeho výpočet sa kvocient odoberie medzi rozptylom údajov ŷi odhadovaných regresným modelom a rozptylom údajov YI zodpovedajúcich každému XI dátových údajov.

R² = Sŷ / sy

postava 1. Korelačný koeficient pre štyri páry dát. Zdroj: f. Zapata.

Ak je 100% údajov na riadku regresnej funkcie, potom bude koeficient určenia 1.

Naopak, ak pre súbor údajov a určitú funkciu úpravy R, koeficient R² Ukázalo sa, že sa rovná 0.5, potom sa dá povedať, že úprava je uspokojivá alebo dobrá na 50%. 

Podobne, keď regresný model vyvolá hodnoty r² Menej ako 0.5, to naznačuje, že zvolená funkcia úpravy sa uspokojivo nepripravuje na údaje, preto je potrebné hľadať ďalšiu funkciu úpravy.

A kedy kovariancia alebo korelačný koeficient Má sklon k nule, potom premenné x a y z údajov nesúvisia, a preto r² bude tiež mať tendenciu k nule.

[TOC]

Ako vypočítať koeficient určenia?

V predchádzajúcej časti sa uviedlo, že koeficient určenia sa vypočíta nájdením kvocientu medzi odchýlkami:

-Odhadované regresnou funkciou premennej a 

-Premenná YI zodpovedajúca každej premennej XI. 

V matematickej podobe zostáva takto:

R² = Sŷ / sy

Z tohto vzorca z toho vyplýva, že r² predstavuje podiel rozptylu vysvetlený regresným modelom. Alternatívne je možné vypočítať R² Prostredníctvom nasledujúceho vzorca, úplne ekvivalentný k predchádzajúcemu:

R² = 1 - (sε / sy)

Kde Sε predstavuje rozptyl odpadu εi = ŷi - yi, zatiaľ čo SY je rozptyl súboru údajov údajov údajov údajov. Na stanovenie ŷi sa použije regresná funkcia, čo znamená potvrdenie, že ŷi = f (xi).

Môže vám slúžiť: frakcia ekvivalentná 3/5 (riešenie a vysvetlenie)

Rozptyl súboru údajov YI, s I od 1 do n, sa počíta týmto spôsobom:

SY = [σ (yi -)² ) / (N-1)]

A potom pokračujte podobným spôsobom pre Sŷ alebo pre Sε.

Ilustratívny prípad

Prostredníctvom detailov spôsobu, akým výpočet Určovací koeficient Berieme nasledujúcu sadu štyroch párov údajov: 

(X, y): (1, 1); (23); (3, 6) a (4, 7).

Pre tento súbor údajov získaných metódou štvorcových minimá je navrhnutá lineárna úprava regresie:

f (x) = 2.1 x - 1 

Pri použití tejto funkcie nastavenia sa získajú rovesníci:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) a (4, 7.4).

Potom vypočítame aritmetický priemer pre x a y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Rozptyl

SY = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Rozptyl sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Koeficient určovania r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interpretácia

Koeficient určenia pre ilustratívny prípad uvažovaný v predchádzajúcom segmente sa ukázal ako 0.98. To znamená, že lineárne nastavenie funkciou:

 f (x) = 2.1x - 1

Je 98% spoľahlivé vysvetliť údaje, ktoré boli získané metódou minimálneho štvorca. 

Okrem koeficientu určenia existuje Korelačný koeficient alebo tiež známy ako Pearson Coefficient. Tento koeficient označený ako r, Vypočíta sa podľa nasledujúceho vzťahu:

R = sxy / (SX SY)

Tu čitateľ predstavuje kovarianciu medzi premennými x a y, zatiaľ čo menovateľ je produktom štandardnej odchýlky pre premennú x a štandardnú odchýlku pre premennú a.

Pearsonov koeficient môže mať hodnoty medzi -1 a +1. Keď tento koeficient má tendenciu k +1, existuje priama lineárna korelácia medzi x a y. Ak namiesto toho má tendenciu -1, existuje lineárna korelácia, ale keď X rastie a klesá. Nakoniec je to blízko 0, medzi týmito dvoma premennými neexistuje korelácia.

Môže vám slúžiť: zoskupené údaje: príklady a vyriešené cvičenie

Je potrebné poznamenať, že koeficient určenia sa zhoduje s štvorcom Pearsonovho koeficientu, iba ak bol vypočítaný prvý na základe lineárneho úpravy, ale táto rovnosť nie je platná pre iné nelineárne úpravy.

Príklady

- Príklad 1

Skupina študentov stredných škôl má v úmysle určiť empirický zákon za obdobie kyvadla ako funkciu jeho dĺžky. Na dosiahnutie tohto cieľa vykonávajú sériu meraní, v ktorých meria čas kyvadla oscilácie pre rôzne dĺžky a získavajú nasledujúce hodnoty:

Dĺžka (m)	Obdobie
0,1	0,6
0,4	1.31
0,7	1,78
1	1,93
1.3	2.19
1.6	2,66
1.9	2.77
3	3,62

Žiada sa, aby sa vytvoril graf disperzie údajov a vykonal lineárnu úpravu regresiou. Okrem toho ukážte regresnú rovnicu a jej koeficient určenia.

Riešenie

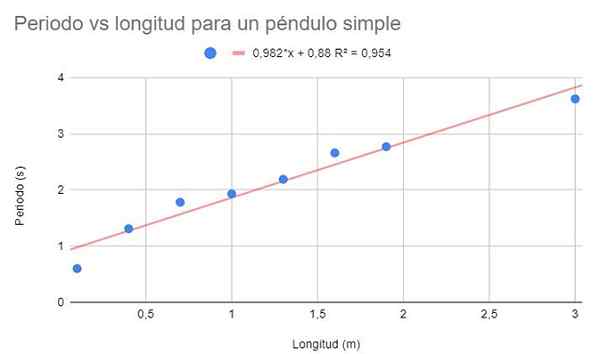Obrázok 2. Grafické riešenie cvičenia 1. Zdroj: f. Zapata.

Je možné pozorovať pomerne vysoký koeficient určenia (95%), takže by sa dalo predpokladať, že lineárne nastavenie je optimálne. Ak sú však body pozorované spolu, zdá sa, že majú tendenciu zakriviť. Tento detail sa v lineárnom modeli neuvažuje.

- Príklad 2

Pre rovnaké údaje z príkladu 1 vytvorte graf disperzie údajov. Pri tejto príležitosti, na rozdiel od príklade 1, sa žiada, aby sa regresná úprava prostredníctvom potenciálnej funkcie.

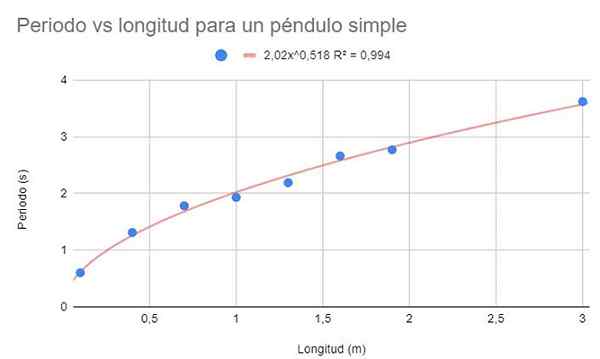Obrázok 3. Grafické riešenie cvičenia 2. Zdroj: f. Zapata.

Tiež ukážte funkciu úprav a jej koeficient určovania r -determinácie².

Riešenie

Potenciálna funkcia je formy f (x) = sekera^B, kde sú A a B konštantné, ktoré sú určené minimálnou štvorcovou metódou.

Predchádzajúci obrázok ukazuje potenciálnu funkciu a jej parametre, ako aj koeficient určenia s veľmi vysokou hodnotou 99%. Upozorňujeme, že údaje nasledujú zakrivenie trendovej čiary.

Môže vám slúžiť: Aditívny princíp

- Príklad 3

S rovnakými údajmi z príkladu 1 a príkladu 2 urobte druhú úpravu polynómu druhého polynomiálu. Zobraziť graf, polynóm nastavenia a koeficient určenia r² korešpondent.

Riešenie

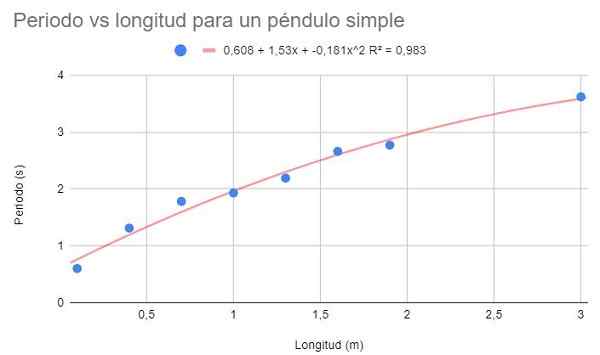Obrázok 4. Grafické cvičenie 3 graf. Zdroj: f. Zapata.

Pri nastavení polynómu druhého stupňa je možné vidieť líniu trendu, ktorý sa dobre hodí k zakriveniu údajov. Podobne je koeficient určenia nad lineárnym nastavením a pod potenciálnym nastavením.

Porovnanie úpravy

Z troch znázornených úprav je jednou s vyšším koeficientom určenia potenciálu (príklad 2).

Potenciálna úprava sa zhoduje s fyzickou teóriou kyvadla, ktorá, ako je známe, uvádza, že obdobie kyvadla je úmerné odmocninovej korene jeho dĺžky, čo je konštanta proporcionality 2π /√g, kde g je zrýchlenie gravitácia.

Tento typ potenciálneho úpravy má nielen najvyšší koeficient určenia, ale konštantný exponent a proporcionalita sa zhodujú s fyzickým modelom. 

Závery

-Úprava regresie určuje parametre funkcie, ktorej cieľom je vysvetliť údaje prostredníctvom minimálnej štvorcovej metódy. Táto metóda spočíva v minimalizácii súčtu kvadratického rozdielu medzi hodnotou a úpravou a hodnotou YI dát pre hodnoty XI dát. Týmto spôsobom sú určené parametre funkcie úpravy.

-Ako sme videli, najbežnejšou funkciou úprav je čiara, ale nie je to jediné, pretože úpravy môžu byť tiež polynomické, potenciálne, exponenciálne, logaritmy a ďalšie. 

-V každom prípade koeficient určenia závisí od údajov a typu úpravy a je to svedectvo o dobrote použitej úpravy.

-Nakoniec koeficient určenia naznačuje percento celkovej variability medzi hodnotou a údajmi vzhľadom na hodnotu ŷ úpravy pre dané x.

Odkazy

1. González C. Všeobecná štatistika. Získané z: Tarwi.La Molina.Edu.pešo
2. IACS. Aragonský inštitút zdravotníctva vied. Zdroj: ICS-Aragon.com
3. Salazar C. a Castillo S. Základné štatistické zásady. (2018). Zdroj: DSPACE.Uce.Edu.ES
4. Superprof. Určovací koeficient. Obnovené z: Superprof.je
5. Usac. Príručka pre opisnú štatistiku. (2011). Získané z: Štatistiky.inžinierstvo.Usac.Edu.Gt.
6. Wikipedia. Určovací koeficient. Obnovené z: je.Wikipedia.com.