Značka triedy

Čo je to značka triedy?

Ten Značka triedy, Známy tiež ako stredný bod, je to hodnota, ktorá je v centre triedy, ktorá predstavuje všetky hodnoty, ktoré sú v tejto kategórii. V zásade sa značka triedy používa na výpočet určitých parametrov, ako je aritmetický priemer alebo štandardná odchýlka.

Potom je značka triedy stredným bodom akéhokoľvek intervalu. Táto hodnota je tiež veľmi užitočná na nájdenie rozptylu súboru údajov už zoskupených do CLAS.

Distribúcia frekvencie

Aby sme pochopili, čo je potrebná značka triedy, koncept distribúcie frekvencie. Vzhľadom na súbor údajov je distribúcia frekvencie tabuľka, ktorá rozdeľuje tieto údaje do niekoľkých kategórií nazývaných triedy.

Táto tabuľka ukazuje, aké je množstvo prvkov, ktoré patria do každej triedy; Ten je známy ako frekvencia.

V tejto tabuľke je súčasť informácií, ktoré získame z údajov.

Na druhej strane získame lepšie porozumenie o súbore údajov, pretože týmto spôsobom je ľahšie oceniť zavedené vzorce, čo uľahčuje manipuláciu s uvedenými údajmi.

Koľko tried uvažuje?

Aby sme urobili distribúciu frekvencie.

Môže vám slúžiť: okraje kocky

Výber, koľko tried by malo byť pohodlne, berúc do úvahy, že malý počet tried môže skryť informácie o údajoch, ktoré chceme študovať, a veľmi veľký môže vygenerovať príliš veľa detailov, ktoré nie sú nevyhnutne užitočné.

Faktory, ktoré musíme vziať do úvahy pri výbere, koľko tried je niekoľko, ale medzi nimi sú dve: prvým je vziať do úvahy, koľko údajov musíme zvážiť; Druhým je vedieť, akú veľkosť je rozsah distribúcie (to znamená rozdiel medzi najväčším a najmenším pozorovaním).

Po už definovaných triedach pokračujeme v spočítaní, koľko údajov v každej triede. Toto číslo sa nazýva frekvencia triedy a označuje sa na opravu.

Ako sme už uviedli, máme distribúciu frekvencie stráca informácie, ktoré pochádzajú jednotlivo z každého údajov alebo pozorovania. Preto sa hľadá hodnota, ktorá predstavuje celú triedu, do ktorej patrí; Táto hodnota je značka Class Mark.

Ako sa získa?

Značka triedy je ústredná hodnota, ktorá predstavuje triedu. Získa sa pridaním limitov intervalu a vydelením tejto hodnoty dvoma. Matematicky by sme to mohli vyjadriť takto:

X_Jo= (Dolná hranica + horná hranica)/2.

V tomto výraze x_Jo Označuje značku I-This Triedy.

Príklad

Vzhľadom na nasledujúci súbor údajov uveďte reprezentatívnu frekvenčnú distribúciu a získajte zodpovedajúcu značku triedy.

Pretože údaje s najvyššou numerickou hodnotou sú 391 a dieťa je 221, máme, že rozsah je 391 -221 = 170.

Môže vám slúžiť: teoretická pravdepodobnosť: ako to dostať von, príklady, cvičenia

Vyberieme 5 tried, všetko s rovnakou veľkosťou. Jedným zo spôsobov, ako zvoliť triedy, je nasledujúci:

Všimnite si, že každé údaje sú v triede, sú disjunct a majú rovnakú hodnotu. Ďalším spôsobom, ako zvoliť triedy, je zvažovanie údajov ako súčasť kontinuálnej premennej, ktorá by mohla dosiahnuť akúkoľvek skutočnú hodnotu. V tomto prípade môžeme zvážiť triedy formulára:

205-245, 245-285, 285-325, 325-365, 365-405

Tento spôsob zoskupenia údajov však môže predstavovať určité nejasnosti s hranicami. Napríklad v prípade 245 vyvstáva otázka: do ktorej triedy patrí, k prvému alebo druhému?

Aby sa predišlo týmto zmätkom, urobí sa dohovor o extrémnych bodoch. Týmto spôsobom bude prvou triedou interval (205 245], druhý (245 285] atď.

Akonáhle sú triedy definované, pokračujeme v výpočte frekvencie a máme nasledujúcu tabuľku:

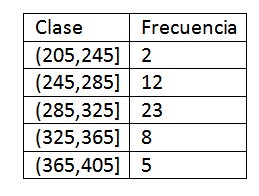
Po získaní frekvenčnej distribúcie údajov pokračujeme v hľadaní značiek tried každého intervalu. Naozaj musíme:

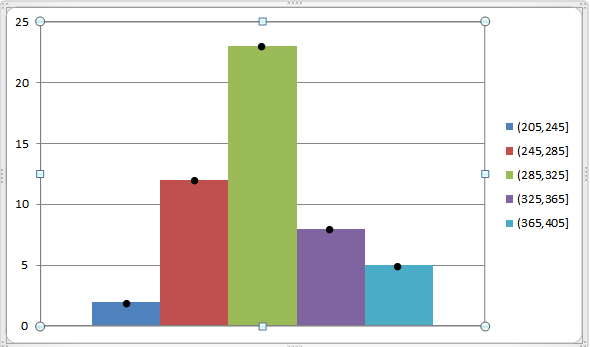
X₁= (205+ 245)/2 = 225

X₂= (245+ 285)/2 = 265          

X₃= (285+ 325)/2 = 305

X₄= (325+ 365)/2 = 345

X₅= (365+ 405)/2 = 385

Môžeme to reprezentovať prostredníctvom nasledujúceho grafu:

Načo to je?

Značka triedy je veľmi funkčná na nájdenie aritmetického priemeru a rozptylu dátovej skupiny, ktorá už bola zoskupená do rôznych tried.

Môžeme definovať aritmetický priemer ako súčet pozorovaní získaných medzi veľkosťou vzorky. Z fyzického hľadiska je jeho interpretácia ako bilančný bod súboru údajov.

Identifikácia celého súboru údajov jedným počtom môže byť riskantná, takže musíte vziať do úvahy rozdiel medzi týmto rovnovážnym bodom a skutočnými údajmi. Tieto hodnoty sú známe ako odchýlka od aritmetického priemeru, a s nimi sa snaží určiť, do akej miery sa aritmetický priemer údajov líši.

Môže vám slúžiť: Frakcie: typy, príklady, vyriešené cvičenia

Najbežnejším spôsobom, ako nájsť túto hodnotu, je z dôvodu rozptylu, ktorý je priemerom štvorcov odchýlok aritmetického priemeru.

Na výpočet aritmetického priemeru a rozptyl súboru údajov zoskupených v triede používame nasledujúce vzorce:

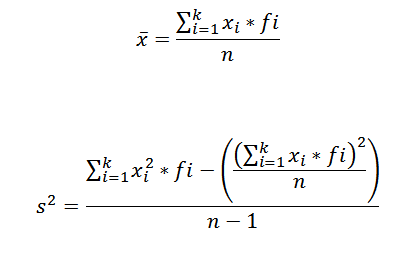
V týchto výrazoch x_Jo  Je to značka I-this Tried, f_Jo predstavuje zodpovedajúcu frekvenciu a K počet tried, v ktorých boli údaje zoskupené.

Príklad

Využitie údajov uvedených v predchádzajúcom príklade musíme rozšíriť o niečo viac údajov v tabuľke distribúcie frekvencie. Získa sa nasledujúce:

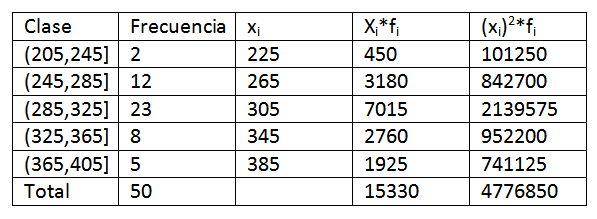
Potom sme nahradením údajov vo vzorci nechali, že aritmetický priemer je:

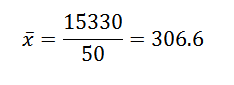
Jeho rozptyl a štandardná odchýlka sú:

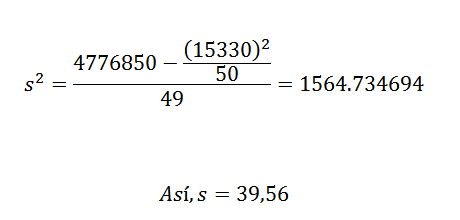
Z toho môžeme vyvodiť záver, že pôvodné údaje majú aritmetický priemer 306,6 a štandardnú odchýlku 39,56.