Celé čísla

Aké sú celé čísla?

Celé čísla predstavujú sadu užitočných čísel na spočítanie úplných objektov, ktoré sa majú a tie, ktoré nie sú. Tiež spočítať tie na jednej strane a na druhej strane určitého referenčného miesta.

Tiež pri celých číslach je možné odčítanie alebo rozdiel vykonať medzi číslom a ďalším väčším ako on, ktorý je usadený napríklad ako dlh, napríklad dlh. Rozdiel medzi ziskami a dlhmi sa robí so znakmi + a - - respektíve.

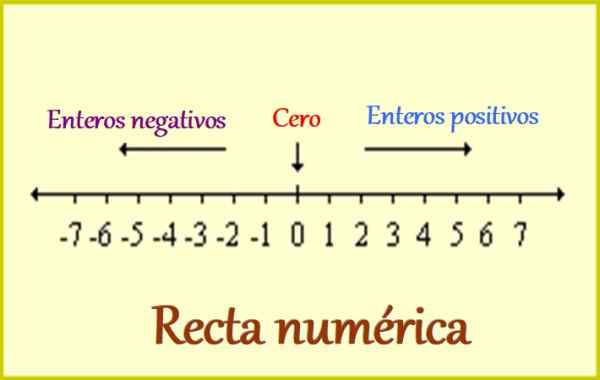
postava 1. Numerická čiara pre celé čísla. Zdroj: Wikimedia Commons. Leomg/CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/3.0).

Preto celé celé čísla obsahuje nasledujúce:

-Pozitívne celé čísla, ktorým je napísané predchádzajúce znamenie A +, alebo jednoducho bez znamenia, pretože sa tiež chápe, že sú pozitívne. Napríklad: +1, +2, +3 ... a tak ďalej.

-0, v ktorom je znamenie irelevantné, pretože ho nepridáva, aby ho odpočítal od určitej sumy. Ale 0 je veľmi dôležitý, pretože je to referencia pre celé čísla: na jednej strane sú kladné a negatívy, ako vidíme na hornej časti obrázku.

-Negatívne celé čísla, ktoré musia byť vždy napísané zo značky -pretože s nimi sú sumy, ako sú dlhy a všetky tie, ktoré sú na druhej strane odkazu. Príklady negatívnych celých čísel sú: -1, -2, -3 ... a od tej doby.

Aké sú celé čísla?

Na začiatku predstavujeme celé čísla s nastavením množiny: z = … -4, -3, -2, -1, 0, +1, +2, +3, +4…, to znamená uvedené a usporiadané. Ale veľmi užitočnou reprezentáciou je to, čo používa numerickú čiaru. Z tohto dôvodu je potrebné nakresliť čiaru, ktorá je zvyčajne vodorovná, na ktorej je 0 označená a rozdelená do rovnakých častí:

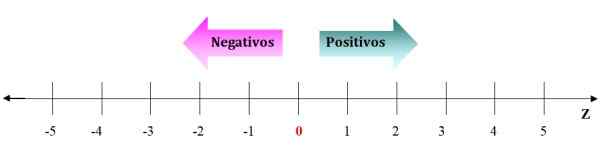Obrázok 2. Zastúpenie celých čísel na číselnom riadku. Od 0 doprava sú kladné celé čísla a od 0 doľava negatíva. Zdroj: f. Zapata.

Negatívy idú doľava z 0 a pozitívne idú doprava. Šípky na číselnom riadku symbolizujú, že čísla naďalej nekonečno. Vzhľadom na akékoľvek celé číslo je vždy možné nájsť ten, ktorý je väčší alebo iný ako nižší.

Absolútna hodnota celého čísla

Absolútna hodnota celého čísla je vzdialenosť medzi číslom a 0. A vzdialenosti sú vždy pozitívne. Preto absolútnou hodnotou záporného celého čísla je číslo bez jeho znamenia menej.

Napríklad absolútna hodnota -5 je 5. Absolútna hodnota je označená ako pruhy takto:

| -5 | = 5

Na jeho vizualizáciu stačí mať priestor na numerickú čiaru od -5 do 0. Zatiaľ čo absolútna hodnota kladného celého čísla je rovnaké číslo, napríklad | +3 | = 3, pretože jeho vzdialenosť k 0 je 3 priestory:

Môže vám slúžiť: Sandwichský zákon: Vysvetlenie a cvičenia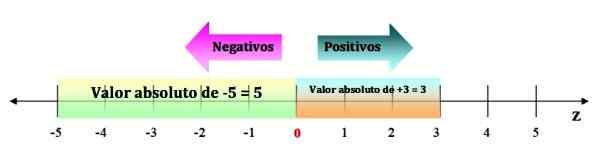Obrázok 3. Absolútna hodnota celého čísla je vždy kladná suma. Zdroj: f. Zapata.

Vlastnosti

-Sada celých čísel je označená ako z a obsahuje súbor prírodných čísel n, ich prvky sú nekonečné.

-Celé číslo a číslo, ktoré nasleduje (alebo číslo, ktoré ho predchádza) sa vždy líši v jednotke. Napríklad po 5 prichádza 6, čo je 1 rozdiel medzi nimi.

-Každé celé číslo má predchodcu a nástupcu.

-Akékoľvek pozitívne celé číslo je väčšie ako 0.

-Negatívne celé číslo je vždy menšie ako 0 a že akékoľvek kladné číslo. Zoberme si napríklad číslo -100, to je menej ako 2, ako 10 a 50. Ale je tiež menej ako -10, -20 a -99 a je väčší ako -200.

-0 nemá žiadne známky, pretože nie je negatívny alebo pozitívny.

-Pri celých číslach je možné vykonať rovnaké operácie, ktoré sa vykonávajú s prírodnými číslami.

-Celý opak k určitému celému číslu X, je -x a súčet celého čísla s jeho opakom je 0:

x + (-x) = 0.

Operácie s celkovými číslami

- Prírastok

-Ak majú čísla pridané rovnaké znamenie, pridajú sa ich absolútne hodnoty a výsledok je uvedený znak, ktorý majú pridané. Tu je niekoľko príkladov:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-V prípade, že čísla sú rôzneho znamenia, absolútne hodnoty (hlavná maloletá) sa odpočítajú a výsledok sa umiestni znak čísla s najvyššou absolútnou hodnotou nasledovne:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Vlastnosti súčtu celých čísel

-Suma je komutatívna, preto poradie dodatkov nezmení sumu. Nech a a b sú dve celé čísla, je splnené, že a+b = b+a

-0 je neutrálny prvok súčtu celých čísel: a + 0 = a

-Akékoľvek celé číslo pridané s jeho opakom je 0. Opak + a je -a a naopak, opak -a es + a. Preto: (+ a)+ (-a) = 0.

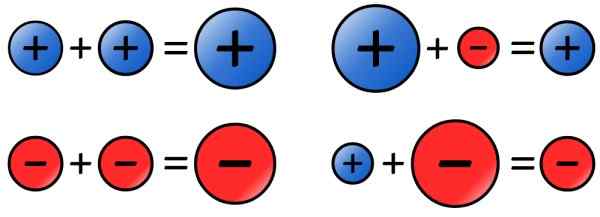Obrázok 4. Pravidlo znamenia pre súčet celých čísel. Zdroj: Wikimedia Commons.

- Odčítanie

Ak chcete odpočítať celé čísla, musíte sa riadiť týmto pravidlom: Odčítanie je rovnocenné so súčtom čísla s jeho opakom. Nechajte dve čísla A a B, potom:

A - b = a + (-b)

Predpokladajme napríklad, že musíte urobiť nasledujúcu operáciu: (-3) - (+7), potom:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Násobenie

Násobenie celých čísel sa riadi určitými pravidlami znakov:

-Produkt dvoch čísel s Rovnaké znamenie Je to vždy pozitívne.

-Keď sa dve čísla vynásobia rôzne príznaky, Výsledok je vždy negatívny.

Môže vám slúžiť: Aké sú časti zlomku? (Príklady)

-Hodnota produktu sa rovná vynásobeniu príslušných absolútnych hodnôt.

Okamžite niekoľko príkladov, ktoré objasňujú vyššie uvedené:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Vlastnosti násobenia celých čísel

-Násobenie je komutatívne. Byť dve celé čísla a a b, je pravda, že: a.B = B.A, ktoré možno tiež vyjadriť ako:

Poradie faktorov nemení produkt.

-Neutrálny prvok násobenia je 1. Byť preto na celé číslo.1 = 1

-Akékoľvek celé číslo vynásobené 0 sa rovná 0: a.0 = 0

Distribučný majetok

Násobenie spĺňa distribučnú vlastnosť vzhľadom na sumu. ÁNO A, B a C sú potom celé čísla:

do.(b +c) = a.B + a.c

Potom príklad, ako uplatniť túto vlastnosť:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Zosilnenie

-Ak je základňa pozitívna, výsledok operácie je vždy pozitívny.

-Ak je základňa záporná, ak je exponent rovnomerný, výsledok je pozitívny. A ak je exponent čudný, výsledok je negatívny.

- Rozdelenie

V divízii sa platia rovnaké pravidlá znakov ako pri násobení:

-Rozdelením dvoch celých čísel toho istého znamenia je výsledok vždy pozitívny.

-Ak sú rozdelené dve celé čísla rôznych príznakov, kvocient je negatívny.

Napríklad:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Dôležitý: Divízia nie je komutatívna, inými slovami na ÷ b ≠ b ÷ a a ako vždy, rozdelenie medzi 0 nie je povolené.

- Zosilnenie

Buďte celé číslo a my ho chceme zdvihnúť na exponent n, potom sa musíme vynásobiť samo osebe, ako je to znázornené nižšie:

doⁿ = a.do.do.do...

Zvážme tiež nasledujúce, berúc do úvahy, že N je prirodzené číslo:

-Ak je A negatívny a n je rovnomerne, výsledok je pozitívny.

-Ak je A negatívny a N je čudné, vedie to k zápornému číslu.

-Ak je A pozitívny a n je párny alebo čudný, vždy je to pozitívne celé číslo.

-Akékoľvek celé číslo zvýšené na 0 sa rovná 1: a⁰ = 1

-Každé číslo vysoké do 1 sa rovná číslu: a¹ = a

Napríklad, že chcete nájsť (-3)⁴ , Aby sa to vynásobilo (-3) štyrikrát sama o sebe, ako je toto: (-3).(-3).(-3).(-3) = 81.

Ďalším príkladom, tiež s negatívnym celým číslom je:

(-2)³ = (-2).(-2).(-2) = -8

Produkt rovnakých základných síl

Predpokladajme, že dve sily rovnakej základne, ak ich vynásobíme, dostaneme inú moc s rovnakou základňou, ktorej exponentom je súčet daných exponentov:

doⁿ ·^m = a^{n + m}

Rovnaký pomer práškového prášku

Oddelením právomocí tej istej základne je výsledkom výkon s rovnakou základňou, ktorej exponentom je odpočítanie daných exponentov:

Môže vám slúžiť: uhly v obvode: typy, vlastnosti, vyriešené cvičenia

doⁿ ÷ a^m = a^{n - m}

Potom dva príklady, ktoré objasňujú tieto body:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Príklady

Pozrime sa na jednoduché príklady na uplatnenie týchto pravidiel a nezabudnite, že v prípade pozitívnych celých čísel je možné znamenie vydať:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

H) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Vyriešené cvičenia

- Cvičenie 1

Mravec sa pohybuje na číselnom riadku na obrázku 1. Počnúc od bodu X = +3 vykonáva nasledujúce posuny:

-7 jednotiek sa presunie doprava

-Teraz sa vráti doľava 5 jednotiek

-Prejdite 3 jednotky vľavo.

-Vráti sa a presúva 4 jednotky doprava.

V akom okamihu je mravec na konci trasy?

Riešenie

Zavolajme na posuny. Keď sú vpravo, dostanú pozitívne znamenie a keď sú na ľavej zápornej značke. Týmto spôsobom a od X = +3 máte:

-Prvý D: x₁ = +3 +7 = +10

-Druhý d: x₂ = +10 +(-5) = +5

-Tretí d: x₃ = +5 +(-3) = +2

-Štvrtý D: x₄ = +2 +4 = +6

Keď končí mravca, jeho chôdza je v polohe x = +6. To znamená, že je to 6 jednotiek napravo od 0 na číselnej čiare.

- Cvičenie 2

Vyriešiť nasledujúcu operáciu:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Riešenie

Táto operácia obsahuje známky zoskupenia, ktoré sú zátvorky, štvorcové zátvorky a kľúče. Pri riešení sa musíte najskôr postarať o zátvorky, po štvorcových zátvorkách a nakoniec kľúče. Inými slovami, musíte pracovať zvnútra von.

V tomto cvičení tento bod predstavuje násobenie, ale v prípade, že medzi jedným číslom a zátvorkou alebo iným symbolom, nemá zmysel, rovnako ako je chápané, že ide o produkt.

Ďalej, rozlíšenie Krok za krokom, farby slúžia ako sprievodca, ktorý sleduje výsledok redukcie zátvoriek, ktoré sú najtlackejšími symbolmi skupiny:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Cvičenie 3

Vyriešte rovnicu prvého stupňa:

12 + x = 30 + 3x

Riešenie

Podmienky sú zoskupené so neznámymi vľavo od rovnosti a číselné výrazy napravo:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9