Inverzné trigonometrické funkcie, odvodené, príklady, cvičenia

Ten Inverzné trigonometrické funkcie, Ako už názov napovedá, sú to zodpovedajúce inverzné funkcie sínusu, kosínutia, dotyčnicovej, cotangent, sušenia a kombajnov.

Inverzné trigonometrické funkcie sú označené rovnakým názvom jej zodpovedajúcej priamej trigonometrickej funkcie plus predpona Oblúk. Teda:

1.- Arcsen (x) Je to inverzná trigonometrická funkcia funkcie hriech

2.- Arccos (x) Je to inverzná trigonometrická funkcia funkcie cos (x)

3.- Arktan (x) Je to inverzná trigonometrická funkcia funkcie Opálenie (x)

4.- Arccot ​​(x) Je to inverzná trigonometrická funkcia funkcie detská postieľka (x)

5.- Arcsec (x) Je to inverzná trigonometrická funkcia funkcie Sec (x)

6.- ARCCSC (x) Je to inverzná trigonometrická funkcia funkcie CSC (x)

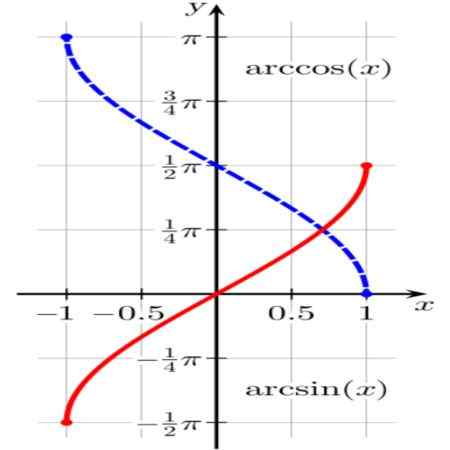
postava 1. Funkcie arcsen (x) (v červenej) a arccos (x) (v modrej). Zdroj: Wikimedia Commons.

Funkcia 9 = arcsen (x) Výsledkom je oblúk jednotky θ (alebo uhol v Radiane θ) také hriech (9) = x.

Napríklad Arcsen (√3/2) = π/3 Pretože je známe, prsník radiánov π/3 sa rovná √3/2.

[TOC]

Hlavná hodnota inverzných trigonometrických funkcií

Takže matematická funkcia f (x) má inverznú g (x) = f^-1x) Je potrebné, aby táto funkcia bola Injekčný, Čo znamená, že každá hodnota a množina príchodu funkcie f (x) pochádzajú z jednej a iba hodnoty x.

Je zrejmé, že táto požiadavka nie je splnená žiadnou trigonometrickou funkciou. Na objasnenie bodu si všimneme, že hodnota y = 0,5 je možné získať z funkcie sínusu nasledujúcimi spôsobmi:

• hriech (π/6) = 0,5
• hriech (5π/6) = 0,5
• hriech (7π/6) = 0,5

A oveľa viac, pretože funkcia sínusu je periodická s periom 2π.

Môže vám slúžiť: násobky 8: Čo je a vysvetlenie

Na definovanie inverzných trigonometrických funkcií je potrebné obmedziť doménu ich zodpovedajúcich priamych trigonometrických funkcií, aby spĺňali požiadavku na injektivitu.

Táto obmedzená doména priamej funkcie bude hlavným rozsahom alebo vetvou jej zodpovedajúcej inverznej funkcie.

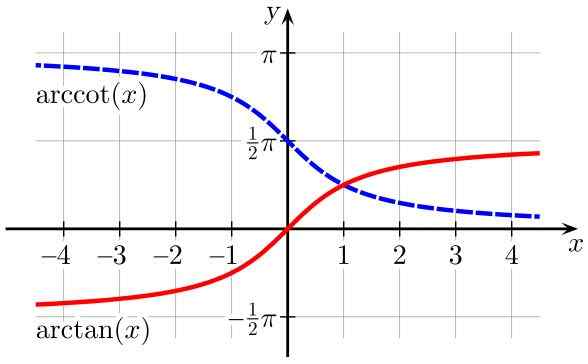Obrázok 2. Arktanové funkcie (x) (v červenej) a arccot ​​(x) (v modrej). Zdroj: Wikimedia Commons.

Tabuľka domén a rozsahov inverzných trigonometrických funkcií

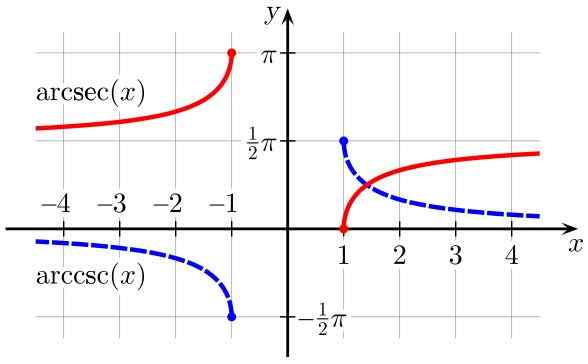Obrázok 3. Arcsec (x) (v červenej) a Arccsc (x) (v modrej) funkcie (v modrej farbe). Zdroj: Wikimedia Commons.

Odvodené z inverzných trigonometrických funkcií

Na získanie derivátov inverzných trigonometrických funkcií sa uplatňujú vlastnosti derivátov, najmä ten, ktorý je odvodený z inverznej funkcie.

Ak označíme f (y) na funkciu a f^-1(x) Na svoju inverznú funkciu sa odvodená z reverznej funkcie týka derivátu priamej funkcie prostredníctvom nasledujúceho vzťahu:

[F^-1(x)] '= 1/ f' [f^-1(X)]

Napríklad: ak x = f (y) = √y je priama funkcia, jej inverzia bude

y = f^-1(x) = x². Uplatňme pravidlo spätného derivátu na tento jednoduchý prípad, aby sme zistili, že toto pravidlo je splnené:

[X²] '= 1 / [√y]' = 1 / (½ a^-½ = 2 a^½ = 2 (x²)^½ = 2x 

Môžeme vyhodnotiť tento trik, aby sme našli tie odvodené z inverzných trigonometrických funkcií.

Napríklad berieme 9 = arcsen (x) Ako priama funkcia bude jej inverzná funkcia hriech (9) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (9)²) =…

… = 1 / √ (1 - x²) .

Týmto spôsobom je možné získať všetky tie odvodené z inverzných trigonometrických funkcií, ktoré sú uvedené nižšie:

Obrázok 4. Tabuľka tých odvodených z inverzných trigonometrických funkcií. Zdroj: Wikimedia Commons.

Tieto deriváty sú platné pre akýkoľvek argument z z komplexných čísel, a preto platia aj pre akýkoľvek skutočný argument X, pretože z = x + 0i.

Môže vám slúžiť: štvornásobné: prvky, vlastnosti, klasifikácia, príklady

Príklady

- Príklad 1

Nájdite Arctan (1).

Riešenie

Arctan (1) je jednotka oblúka (uhol v radiánoch) ፀ tak, že opálenie (ፀ) = 1. Tento uhol je ፀ = π/4, pretože SO (π/4) = 1. Potom Arctan (1) = π/4.

- Príklad 2

Vypočítajte oblúk (cos (π/3)).

Riešenie

Uhol π/3 radiány je pozoruhodný uhol, ktorého kosínus je ½, takže problém sa zredukuje na nájdenie oblúka (½).

Takže je to o nájdení uhol, ktorého sine dá ½. Tento uhol je π/6, pretože sen (π/6) = sen (30 °) = ½. Preto arcsen (cos (π/3)) = π/6. 

Cvičenia

- Cvičenie 1

Nájdite výsledok nasledujúceho výrazu:

Sec (Arcan (3)) + CSC (ARCCOT (4))

Riešenie

Začneme pomenovať a = arcan (3) a p = arcot (4). Takže výraz, ktorý musíme vypočítať, je taký:

SEC (a) + CSC (p)

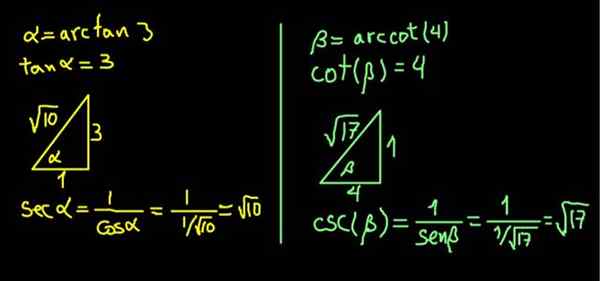
Expresia a = arcan (3) je rovnocenná s príslovím SO (a) = 3.

Pretože dotyčnica je opačná noha na susednom susedstve, je vytvorený obdĺžnikový trojuholník Cateto na rozdiel od a z 3 jednotiek a susedná kategória jednotky 1 jednotky, takže (α) = 3/1 = 3.

V obdĺžnikovom trojuholníku je hypotenus určená vetou Pythagoras. S týmito hodnotami je to √10, takže:

sec (a) = hypotenus / susedný kateto = √10 / 1 = √10.

Podobne β = arcot (4) je ekvivalentné uvádzaniu, že COT (β) = 4.

Postavený obdĺžnikový trojuholník kateta susediaceho s β 4 jednotiek a opačným katetom 1 jednotky, takže COT (β) = 4/1.

Trojuholník je okamžite dokončený nájsť svoju hypotenus vďaka Pythagorasovej vete. V tomto prípade sa ukázalo, že má √17 jednotiek. Potom sa vypočíta CSC (β) = hypotenus / opačný kateto = √17 / 1 = √17.

Môže vám slúžiť: y = 3sen (4x) funkčné obdobie

Pamätajte si, že výraz, ktorý musíme vypočítať, je: 

Sec (Arcan (3)) + CSC (Arcot (4)) = SEC (a) + CSC (β) =…

… = √10 + √17 = 3,16 + 4,12 = 7,28.

- Cvičenie 2

Nájdite riešenia:

Cos (2x) = 1 - sen (x)

Riešenie

Je potrebné, aby boli všetky trigonometrické funkcie vyjadrené v rovnakom argumente alebo uhle. Použijeme identitu dvojitého uhla:

Cos (2x) = 1 - 2 sen²(X)

Potom sa pôvodný výraz zredukuje na:

1 - 2 sen²(x) = 1 - hriech x

Po zjednodunutí a faktorizovaní je vyjadrený ako:

Sin (x) (2 sen (x) - 1) = 0

Čo vedie k vzniku dvoch možných rovníc: sin (x) = 0 s riešením x = 0 a ďalšou rovnicou sen (x) = ½ s x = π/6 ako riešenie.

Riešenia zvýšenej rovnice sú: x = 0 alebo x = π/6.

- Cvičenie 3

Nájdite riešenia nasledujúcej trigonometrickej rovnice:

cos (x) = hriech²(X)

Riešenie

Na vyriešenie tejto rovnice je vhodné umiestniť jeden typ trigonometrickej funkcie, takže použijeme základnú trigonometrickú identitu tak, aby bola pôvodná rovnica prepísaná nasledovne:

cos (x) = 1 - cos²(X)

Ak pomenujeme y = cos (x), výraz môže byť prepísaný ako:

a² + a - 1 = 0

Je to rovnica druhého stupňa v a ktorých riešenia sú:

y = (-1 ± √5) / 2

Potom hodnoty X, ktoré spĺňajú pôvodnú rovnicu, sú:

X = Arcos ((-1 ± √5) / 2)

Skutočným riešením je kladná značka x = 0,9046 rad = 51,83 °.

Ďalším riešením je komplex: x = (π - 1,06 i) rad.

Odkazy

1. Hazardinkel, m. 1994. Encyklopédia matematiky. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Mobilný kamarát. Inverzné trigonometrické funkcie. Získané z: Matemovil.com
3. Vesmír. Inverzné trigonometrické funkcie. Získané z: Universoformulas.com
4. Weisstein, Eric W. Vynaložiť trigonometrické funkcie. Obnovené z: Mathworld.Valfram.com
5. Wikipedia. Vynaložiť trigonometrické funkcie. Zdroj: In.Wikipedia.com