Vzorec a rovnice náhodného chýb, výpočet, príklady, cvičenia

On náhodná chyba fyzického sumy pozostáva z nepredvídateľných variácií miery tejto sumy. Tieto variácie môžu byť produkované fenoménom, ktorý sa meria, meracie prístroj alebo samotným pozorovateľom.

Takáto chyba nie je spôsobená skutočnosťou, že počas experimentu sa niečo stalo zle, ale že je to chyba spojená s procesom merania alebo študovaným javom. To spôsobuje merané opatrenie niekedy o niečo väčšie a niekedy o niečo nižšie, ale zvyčajne osciluje okolo centrálnej hodnoty.

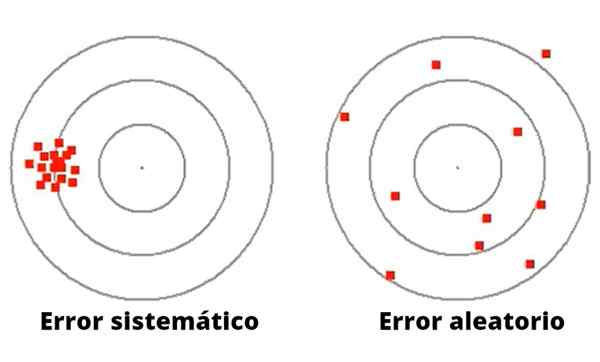
Obrázok 1- náhodné chyby sa líšia v rozsahu a smeru. Naopak, systematické chyby majú tendenciu byť konzistentné.

Na rozdiel od náhodných chýb môže byť systematická chyba spôsobená zlou kalibráciou alebo nevhodným faktorom mierky v meraní prístroja vrátane zlyhania v experimentálnych zariadeniach alebo nevhodného pozorovania, ktoré spôsobuje odchýlku v rovnakom zmysle.

Obrázok 1 zobrazuje rozdiel medzi systematickou a náhodnou chybou v hre spustenia DART do cieľa s kruhmi.

V prípade ľavej strany sú šípky sústredené okolo veľmi ďaleko od stredu. Džbán týchto šípok, hoci je dobrým cieľom, má systematické zlyhanie, možno vizuálneho pôvodu alebo v ceste hádzania.

Na druhej strane, džbán vpravo (na obrázku 1) má veľkú disperziu okolo centrálneho cieľa, preto je to veľmi nepresný džbán so zlým cieľom, ktorý nedobrovoľne robí náhodnú chybu.

[TOC]

Vzorce a rovnice v náhodnej chybe

Keď proces merania vykazuje náhodnú chybu, je to potrebné.

Pri každom meraní je samozrejme potrebné postarať sa o to, že podmienky, v ktorých sa vykonávajú, sú vždy rovnaké.

Môže vám slúžiť: Faradayov zákon: vzorec, jednotky, experimenty, cvičenie,

Predpokladajme, že meranie sa opakuje n časy. Pretože v každom meraní je náhodná chyba, bude mierne iná hodnota. Predpokladajme, že súbor n Merania sú:

X₁, X₂, X₃,…, X_n

Aká správa hodnoty pre mieru? 

Priemerná hodnota a štandardná odchýlka

Ten stredná hodnota ani priemer súboru opatrení, ktoré označujeme a počíta sa takto:

= (x₁ + X₂ + X₃ +… +X_n) / n

Štandardná odchýlka

Tento výsledok má však maržu chyby danej štandardnou odchýlkou. Aby ste to definovali, musíte najprv poznať odchýlku a potom rozptyl:

-Odchýlka d_Jo  že každá nameraná hodnota má Xi Pokiaľ ide o priemernú hodnotu, je:

d_Jo = x_Jo -

Keby sa vypočítal priemer odchýlok, systematicky by sa získal = 0, vzhľadom na to: 

= (d₁ + d₂ + d₃ +… +D_n) /n =

= [x₁ - ) + (x₂ - ) +… +(X_n - )]/n

= (x₁+ X₂ +… + X_n) / n - n / n = - = 0

-Priemer odchýlok nie je užitočné poznať rozptyl opatrení. Na druhej strane, priemerná hodnota štvorca odchýlok alebo rozptylu, označená σ², Áno, je.

Vypočíta sa podľa nasledujúceho vzorca:

σ² = (d₁² + d₂² +.. .+ d_n² ) / (N -1)

V štatistike sa táto suma nazýva rozptyl.  

A na druhej odmocnine rozptylu je známy ako Štandardná odchýlka σ:

σ = √ [(D₁² + d₂² +.. .+ d_n² ) / (n -1)] 

Štandardná odchýlka σ naznačuje, že:

1.- 68% vykonaných meraní je zahrnutých do intervalu [ - σ, + σ]. 

2.- 95% meraní je v intervale [ - 2σ, + 2σ].

3.- 99,7% prijatých opatrení je v rozsahu [ - 3σ, + 3σ].

Ako vypočítať náhodnú chybu?

Výsledkom merania je stredná hodnota z n Merania označené a vypočítané podľa nasledujúceho vzorca:

Môže vám slúžiť: Areolar Speed: Ako sa vypočítava a vyrieši

= (∑x_Jo) / n

Nie je to však „presná“ hodnota merania, pretože je ovplyvnená náhodná chyba ε, čo sa počíta takto:

ε = σ / √n

Kde:

σ = √ [(∑ (xi -)² ) / (n -1)]

Konečný výsledok merania musí byť nahlásený niektorým z nasledujúcich spôsobov:

1. ± σ / √n = ± ε S úrovňou dôvery 68%.
2. ± 2σ / √n = ± 2ε S 95% úrovňou spoľahlivosti.
3. ± 3σ / √n = ± 3ε S úrovňou dôvery 99,7%.

Náhodná chyba ovplyvňuje posledný významný údaj o meraní, ktorý sa zvyčajne zhoduje s ocenením meracieho prístroja. Ak je však náhodná chyba veľmi veľká, posledné dve významné číslice môžu byť ovplyvnené variáciou.

Príklady náhodných chýb

Náhodné chyby sa môžu objaviť v rôznych prípadoch, v ktorých sa vykonáva opatrenie:

Meranie dĺžky pomocou pásky alebo pravidla

Ak sa dĺžka meria pomocou pravidla alebo pásky a hodnoty spadajú medzi značky stupnice, potom sa odhaduje táto stredná hodnota.

Niekedy má odhad nadbytok a inú chybu, takže do procesu merania sa zavádza náhodná chyba.

Obrázok 2. Náhodné chyby sa môžu objaviť, keď sa dĺžka meria pomocou páskovej pásky. Zdroj: Pikrepo.

Rýchlosť vetra

Pri meraní rýchlosti vetra môžu nastať zmeny v čítaní z jedného momentu na druhý kvôli meniacej sa povahe javu.

Pri čítaní objemu v odstupňovanom valci

Keď sa objem číta s odstupňovaným valcom, dokonca sa snaží minimalizovať chybu paralage, zakaždým, keď sa zmerala, sa uhol meniskálneho pozorovania zmení trochu, a preto sú opatrenia ovplyvnené náhodnou chybou.

Môže vám slúžiť: Prvá rovnovážna podmienka: Vysvetlenie, príklady, cvičenia Obrázok 3.- V chémiovom laboratóriu je možné urobiť náhodné chyby pri čítaní valca pre postgraduálny valc. Zdroj: pexels.

Keď sa meria postava dieťaťa

Zmeraním výšky dieťaťa, najmä ak je trochu nepokojná, spôsobuje, že malé zmeny držania tela sa mierne zmenia čítanie.

Pri používaní kúpeľňovej stupnice

Keď chceme zmerať našu váhu s kúpeľňou, malá zmena v podpornom bode, dokonca aj zmena polohy môže náhodne ovplyvniť meranie.

Cvičenie

Hračkársky kočík sa nechá valiť sa pozdĺž rovnej a naklonenej trate a meraná s stopkami, ktorý berie celú stopu. 

Meranie sa vykonáva 11 -krát, s starostlivosťou o uvoľnenie košíka z toho istého miesta, bez toho, aby ste dali impulz a ponechali si opravy sklonu.

Sada získaných výsledkov je:

3,12S 3,09S 3,04 s 3,04 s 3,10S 3,08S 3,05S 3,10S 3,11S 3,06S, 3,03S

Aká je náhodná chyba opatrení?

Obrázok 4. Urobte si čas hračky, ktorá zostupuje cez naklonenú rovinu. Zdroj: Fanny Zapata.

Riešenie

Ako je vidieť, získané výsledky nie sú jedinečné a mierne sa líšia.

Prvým je výpočet priemernej hodnoty času zostupu, získanie 3,074545455 sekúnd.

Nemá zmysel udržiavať toľko desatinných miest, pretože každé meranie má tri významné čísla a druhé desatinné miesto každého opatrenia je neisté, pretože je na hranici ocenenia stopiek, preto je výsledok zaokrúhlený na dve desatinné miesta:

= 3,08 s.

S kalkulačkou v štatistickom režime je štandardná odchýlka σ = 0,03 s A štandardná chyba je σ / √11 = 0,01 s. Konečný výsledok je vyjadrený takto:

Čas 

3,08 s ± 0,01 s (s úrovňou spoľahlivosti 68%)

3,08 s ± 0,02 s (s 95%úrovňou spoľahlivosti)

3,08 s ± 0,03 s (s úrovňou spoľahlivosti 99,7%)

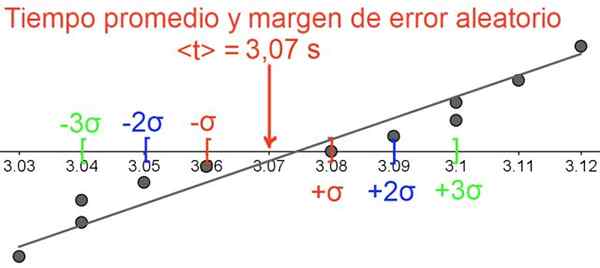Obrázok 5. Náhodná chyba, všimnite si, že údaje sú zoskupené okolo priemernej hodnoty. Zdroj: f. Zapata.

Odkazy

1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Helmestine a. Náhodná chyba vs. Systematická chyba. Zotavené z: Thoughtco.com
4. Laredo, e. Stredné chyby. Získané z: USB.ísť.
5. Levin, r. 1988. Štatistiky pre administrátorov. Druhý. Vydanie. Sála.