Nadmerná funkcia, vlastnosti, príklady

A nadmerná funkcia Je to akýkoľvek vzťah, v ktorom je každý prvok patriaci k Codominium obrazom aspoň jednej doménovej prvku. Tiež známa ako funkcia o, Sú súčasťou klasifikácie funkcií týkajúcich sa spôsobu, akým sú ich prvky spojené.

Napríklad funkcia F: a → B definovaný F (x) = 2x

Čo je čítané “F to je od Do až do B definovaný F (x) = 2x "

Dotknite sa definovať sady štartovacích a príchodov A b.

A: 1, 2, 3, 4, 5 Teraz hodnoty alebo obrázky, ktoré budú každý z týchto prvkov zverejnené, keď sa hodnotia v F, Budú to prvky kodominia.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Tým sa vytvorí množina B: 2, 4, 6, 8, 10

Potom sa dá uzavrieť, že:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 definovaný F (x) = 2x je nadmerná funkcia

Každý prvok kodomíniu musí byť aspoň jednou operáciou nezávislej premennej prostredníctvom príslušnej funkcie. Neexistuje žiadny obmedzujúci obraz, prvok kodomíniu môže byť obrazom viac ako jedného prvku domény a pokračovať v riešení a nadmerná funkcia.

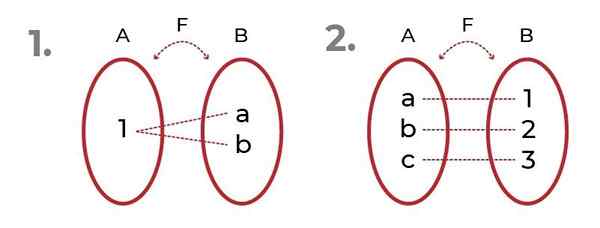
Obrázok zobrazuje 2 príklady s injekčné funkcie.

Zdroj: autor

V prvom je pozorované, že obrázky možno odkazovať na rovnaký prvok, bez toho, aby sa ohrozili Nadmernosť funkcia.

V druhom vidíme spravodlivé rozdelenie medzi doménou a obrázkami. To vedie k vzniku Bijektívna funkcia, kde kritériá Injekčná funkcia a nadmerná funkcia.

Iná metóda identifikácie injekčné funkcie, je overiť, či sa kodomínium rovná hodnosti funkcie. To znamená, že ak sa sada príchodu rovná obrázkom poskytovaným funkciou pri hodnotení nezávislej premennej, Funkcia je nadmerná.

[TOC]

Vlastnosti

Zvážiť Nadmerný Na funkciu sa musí splniť nasledujúce:

Byť F: D_F → C_F

∀ B ℮ C_F  A do ℮  D_F   / F (a) = b

Toto je algebraický spôsob, ako to zistiť Pre všetky „b“, ktoré patrí do C_F Existuje „A“, ktorý patrí D_F  tak, že funkcia F vyhodnotená v „A“ sa rovná „B“. 

Môže vám slúžiť: radikálne vlastnosti

Nadmerná je zvláštnosť funkcií, kde sú kodomínium a hodnosť podobné. Prvky vyhodnotené vo funkcii teda tvoria sadu príchodu.

Kondicionovanie funkcií

Niekedy funkcia, ktorá nie je Nadmerný, môže podstúpiť určité kondicionovanie. Tieto nové podmienky môžu zmeniť na a nadmerná funkcia.

Všetky typy modifikácií domény a kodomínium funkcie sú platné, kde cieľom je splniť vlastnosti nadmernej prípravy v príslušnom vzťahu.

Príklady: Vyriešené cvičenia

Na splnenie podmienok Nadmernosť Mali by sa uplatňovať rôzne techniky kondicionovania, aby sa zabezpečilo, že každý prvok kodomínium je v súprave obrázkov funkcie.

Cvičenie 1

• Byť funkciou F: r → R definovaný riadkom F (x) = 8 - x

Odpoveď: [všetky skutočné čísla]

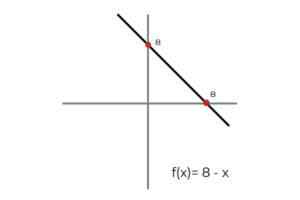Zdroj: autor

V tomto prípade funkcia popisuje kontinuálnu čiaru, ktorá pokrýva všetky skutočné čísla vo svojej doméne aj v rozsahu. Pretože hodnosť funkcie R_F Je to rovnaké ako kodominium R Dá sa dospieť k záveru, že:

F: r → R definovaný riadkom F (x) = 8 - x je a nadmerná funkcia.

Platí to pre všetky lineárne funkcie (funkcie, ktorých väčší stupeň premennej je jeden).

Cvičenie 2

• Študovať funkciu F: r → R definovaný F (x) = x² : Definujte, či je a nadmerná funkcia. V prípade, že to tak nie je, ukážte potrebné kondicionovanie, aby sa jeho vpred.

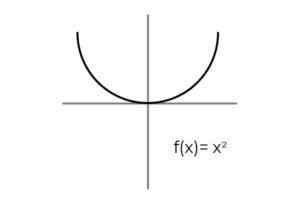Zdroj: autor

Prvá vec, ktorú treba zvážiť, je kodominium F, ktoré pozostávajú zo skutočných čísel R. Neexistuje spôsob, ako funkcia vyhodiť zápornú hodnotu, ktorá vylučuje negatívne skutočné medzi možnými obrázkami.

Kondicionovanie intervalového kodomínium [0 , ∞ ]. Zabráni sa opustiť prvky Co -alomio bez toho, aby sa prepletali cez F.

Obrázky sa opakujú pre páry prvkov nezávislej premennej, ako napríklad x = 1 a x = - 1.  Ale to ovplyvňuje iba Injekčnosť  funkcie, nie je to problém pre túto štúdiu.

Môže vám slúžiť: následné deriváty

Týmto spôsobom možno dospieť k záveru, že:

F: r  →[0, ∞ ) definovaný F (x) = x²    Je to nadmerná funkcia

Cvičenie 3

• Definujte podmienky kodomínium, ktoré by nadmerný do funkcií

F: r  → R definovaný F (x) = sin (x)

F: r  → R definovaný F (x) = cos (x)

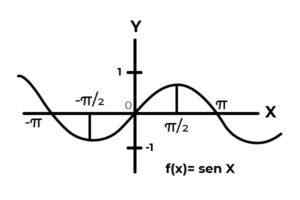Zdroj: autor 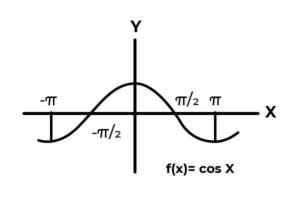Zdroj: autor.

Správanie trigonometrických funkcií je podobné správaniu vĺn, pričom je veľmi bežné nájsť opakovania závislej premennej medzi obrázkami. Vo väčšine prípadov je rozsah funkcie obmedzený na jeden alebo viac sektorov skutočnej línie.

Toto je prípad sínusových a kosínutých funkcií. Kde ich hodnoty kolísajú v intervale [-1, 1]. Uvedený interval musí kondicionovať kodominium, aby sa dosiahol obálku funkcie.

F: r  →[-eleven] definovaný F (x) = sin (x)  Je to nadmerná funkcia

F: r  →[-eleven]definovaný F (x) = cos (x) Je to nadmerná funkcia

Cvičenie 4

• Študovať funkciu

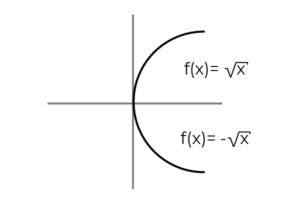
F: [0, ∞ ) → R definovaný F (x) = ± √x   Označte, či je a nadmerná funkcia

Zdroj: autor

Funkcia F (x) = ± √x  Má špecifickosť, ktorá definuje 2 závislé premenné pri každej hodnote „x“ . To znamená, že rozsah prijíma 2 prvky pre každý, ktorý sa vykonáva v doméne. Pozitívna a záporná hodnota pre každú hodnotu „x“ sa musí overiť pre každú hodnotu „x“.

Pri pozorovaní počiatočnej zostavy sa poznamenáva, že doména už bola obmedzená, aby sa predišlo neurčitým vytvoreným pri hodnotení záporného čísla v koreni krútiaceho momentu.

Pri overovaní rozsahu funkcie ukazuje, že každá hodnota kodominium patrí do rozsahu.

Týmto spôsobom možno dospieť k záveru, že:

F: [0, ∞ ) → R definovaný F (x) = ± √x  Je to nadmerná funkcia

Môže vám slúžiť: Súbežné vektory: Charakteristiky, príklady a cvičenia

Cvičenie 4

• Študovať funkciu F (x) = ln x  Označte, či je a nadmerná funkcia. Podmieňujte súpravy príchodu a odchodu na prispôsobenie funkcie kritériám nadmernej prípravy.

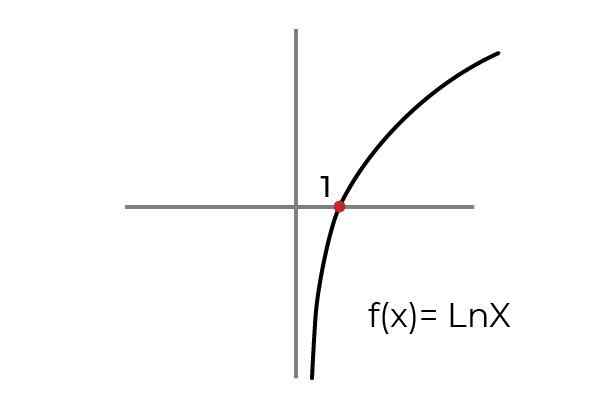Zdroj: autor

Ako je znázornené v grafe, funkcia F (x) = ln xje definovaný pre hodnoty „x“ väčšie ako nula. Zatiaľ čo hodnoty „a“ ​​alebo obrázkov môžu mať akúkoľvek skutočnú hodnotu.

Týmto spôsobom môžeme obmedziť doménu F (x) = do intervalu (0 , ∞ )

Zatiaľ čo hodnosť funkcie je možné udržiavať ako sada reálnych čísel R.

Vzhľadom na to možno dospieť k záveru, že:

F: [0, ∞ ) → R definovaný F (x) = ln x  Je to nadmerná funkcia

Cvičenie 5

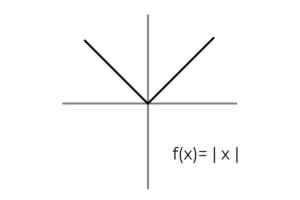
• Štúdium Absolútna hodnota funkcia F (x) = | X | a určiť súpravy príchodu a odchodu, ktoré sa zhromažďujú podľa kritérií pre vernosť.

Zdroj: autor

Doména funkcie je splnená pre všetky skutočné čísla R. Týmto spôsobom je potrebné vykonať jediné kondicionovanie v kodomínii, pričom sa zohľadňuje, že funkcia absolútnej hodnoty má iba kladné hodnoty.

Kodominium funkcie sa stanoví, aby sa vyrovnal podľa rovnakého rozsahu

[0 , ∞ )

Teraz možno dospieť k záveru, že:

F: [0, ∞ ) → R definovaný F (x) = | X |  Je to nadmerná funkcia

Navrhované cvičenia

1. Overte, či sú nasledujúce funkcie nadmerné:

• F: (0, ∞ ) → R definovaný F (x) = log (x + 1)
• F: r → R definovaný F (x) = x³
• F: r →[1, ∞ )  definovaný F (x) = x²  + 1
• [0, ∞ ) → R definovaný F (x) = log (2x + 3)
• F: r → R definovaný F (x) = sec x
• F: r - 0 → R definovaný F (x) = 1 / x

Odkazy

1. Úvod do logiky a kritického myslenia. Merrilee H. Losos. University of Pittsburgh
2. Problémy v matematickej analýze. Piotr Bilar, Alfred Witkowski. Wroclaw University. Pól.
3. Prvky abstraktnej analýzy. Mícheál O'Searcoid PhD. Oddelenie matematiky. University College Dublin, Beldfield, Dublind 4
4.  Úvod do logiky a metodológie deduktívnych vied. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Matematické analýzy. Enrique Linés escardó. Redaktor. Do roku 1991. Barcelona, ​​Španielsko.